基于优先执行关系闭包运算的事务可串行化判定方法
熊中敏 王佳艳 汪 博 陈 明
(上海海洋大学信息学院 上海 201306)(农业部渔业信息重点实验室 上海 201306)
0 引 言
随着移动互联网和数字化操作平台的发展,信息系统都支持并发用户,从而产生了大量的并发事务[1-3]。为了提高系统的性能,现代数据库技术支持并发事务的调度执行;为了维护整个系统上操作的正确性,必须确保并发事务调度是可串行化调度。并发事务的可串行化检测是事务并发管理的一项重要任务,也是系统执行并发控制的前提[4-6]。
当前事务管理的研究大量集中在对新型应用中出现的新事务的并发控制协议的研究上,以便确保并行事务执行的可串行化调度。但对并行事务调度是否具有可串行化的判定,仍然基于传统的执行图的判定方法[7-9]。执行图的判定方法原理比较简单,首先判断在一个调度中、并发冲突事务集合中事务之间的执行优先关系,然后以有向图这种数据结构存储:事务表示为图中的节点,事务之间的执行优先关系表示为节点之间的有向边;在建立好完全的图结构后,通过图搜索方法遍历整个图,如果图中不存在环这种结构,就判断并发事务集的当前调度是可串行化的,否则就是不可串行化的。要实现这种传统的判定方法,需要建立复杂的图数据结构,并要建立便于图中节点的遍历和回溯的索引结构来实现图的搜索[10],直接的图搜索算法没有相应的环的识别,还需要改进的图搜索算法来支持环的识别。
本文从关系运算的代数方法出发,提出了基于事务执行优先关系的闭包运算和由此建立的联合逻辑公式的计算,通过逻辑判定来检验并发事务的可串行化。通过定理证明和实例验证,所提出的基于逻辑公式的代数判定方法取得了同执行图判定相同的效果,而且判定更直观,更易于操作实现,不需要建立复杂的图数据结构和在图搜索中检测环是否出现。
1 定义及概念
1.1 事务的并发调度及可串行化调度
例如:从账户A向账户B转账1 000元,系统查找到账户A,检查账户的余额大于1 000时,读出余额并从中减去1 000元,然后把减去的余额写回到A账户中。找到B账户,读出B账户余额后加上1 000元,再把加后的余额写回到B账户中。这一系列的过程要么全部都发生,要么全不发生,这就是事务。
定义1[11]事务(Transaction)是构成单一逻辑工作单元的操作集合,要么完整的执行,要么完全不执行。无论发生何种情况,DBS必须保证事务能正确、完整的执行。
以银行系统中多个事务对多个账户进行存取操作为例。事务T1从账户A转100元到账户B,定义如下:
T1:Read(A);A:=A-100;Write(A);Read(B);
B:=B+100;Write(B);
T2从账户A中转10%的存款到账户B,定义如下:
T2:Read(A);X=A×0.1;A:=A-X;Write(A);
Read(B);B:=B+X;Write(B)
如系统先执行T1的前3条指令,然后转向T2,并执行它的前四条指令,接着再转向T1,执行T1的后3条指令,最后转向T2,执行它的后3条指令。在这种类型的执行顺序中,两个事务的指令交替执行,称为并发调度。
定义2[11]事务的执行次序称为调度。如果多个事务依次执行,则称为事务的串行调度;如果利用分时的方法同时处理多个事务,称为事务的并发调度。
定义3[12]如果事务的并发调度对数据库状态的影响与某个串行调度相同,那么这个并发调度能保持数据库状态的一致,这样的调度是正确的,并称为可串行化调度。
一个可串行化的并发调度与某个串行调度对数据库的影响相同。例如文献[12]定义了两个事务T1、T2,两个数据项A、B,初始状态都为50。事务T1、T2的定义及其一个串行化调度如图1所示,将图1中的调度称为调度1。

T1T2Read(A)A:=A+100Write(A)Read(B)B:=B+100Write(B)Read(A)A:=A∗2Write(A)Read(B)B:=B∗2Write(B)
图1 串行化调度1:T1先于T2执行
再给出这两个事务的并发调度的例子,如图2所示,图2的调度称为调度2。
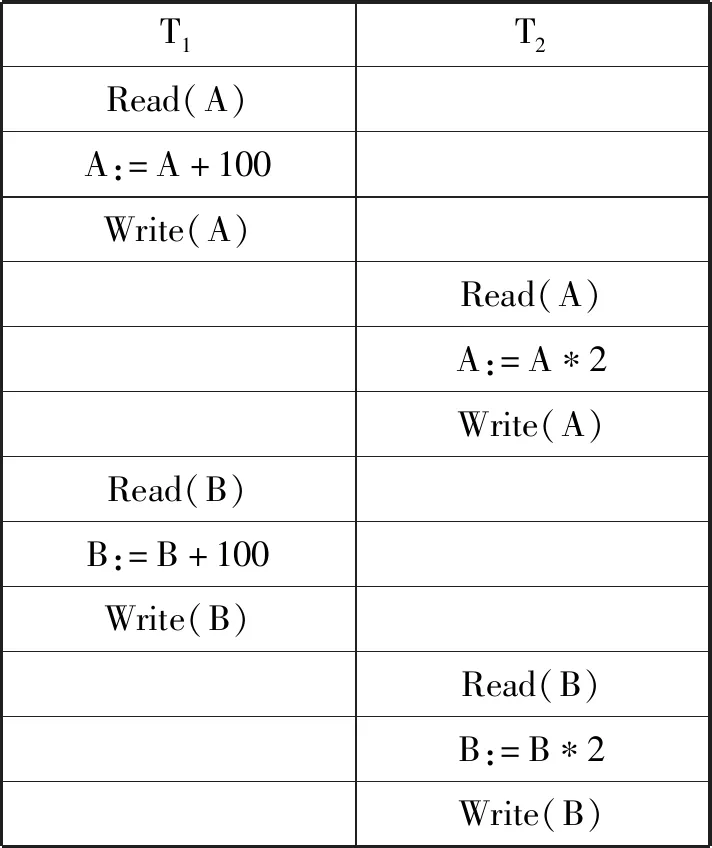
T1T2Read(A)A:=A+100Write(A)Read(A)A:=A∗2Write(A)Read(B)B:=B+100Write(B)Read(B)B:=B∗2Write(B)
图2 并发调度2
通过对并发调度2分析可知,由于T1中的操作“Read(B);B:=B+100;Write(B)”和T2中的操作“Read(A);A:=A*2;Write(A)”可以非冲突交换(即相邻操作交换执行的先后次序不会影响操作的结果)至先执行T1后执行T2,即调度2对数据库状态的影响与调度1是相同的,故它是一个可串行化的并发调度[12]。
定义4[12]对于两个调度S1和S2,如果S1的一系列相邻动作经过非冲突交换能转换成S2;同样地,如果S2的一系列相邻动作经过非冲突交换能转换成S1,则这两个调度是冲突等价的。当一个调度冲突等价于一个串行调度时,这个调度就是冲突可串行化的。
调度2冲突等价于调度1,而且调度2是冲突可串行化的。
1.2 基于执行图的冲突可串行化判定
判断一个调度是否是冲突可串行化,只要检查该调度中出现冲突的操作的顺序是否与一个串行调度中出现的顺序相同即可。如果相同,则说明是冲突可串行化的;如果不同,就不是冲突可串行化的。
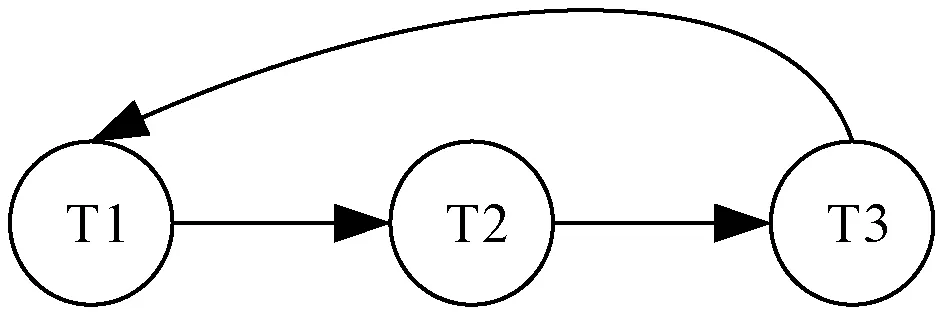
定义5[12]已知调度S,其中事务T1、T2,如果T1的动作A1和T2的动作A2满足下面的情况,则T1的执行优先于T2,记为T1 (1) 在调度S中,A1在A2前; (2)A1和A2都涉及同一个数据库元素; (3)A1和A2中至少有一个是写。 此时,任何一个与S冲突等价的调度中,A1都要出现在A2前。如果这个调度是与S冲突等价的串行调度,则T1一定出现在T2前。所以只要检查出一个调度中任何两个冲突操作的顺序,并确定其是否与冲突等价的串行调度中的事务的顺序相同。如果相同,该调度就是可串行化调度[12]。 定义6[12]优先图由节点和有向弧两种元素构成,节点代表事务,有向弧表示事务执行的先后次序。如果T1 利用优先图判断是否是冲突可串行化的准则:如果调度S的优先图中没有环,则S是冲突可串行化的,如果优先图中有环,则S不是冲突可串行化的[12]。 例1下面的调度由3个事务T1、T2、T3的动作构成[12]: S1:r2(A);r1(B);w2(A);r3(A);w1(B);w3(A);r2(B);w2(B) 在调度S中,可以找到的相邻冲突操作有w2(A)和r3(A),w1(B)和r2(B)。w2(A)在r3(A)前,说明T2 图3 调度S1的执行图 如果将调度S1中r2(B)向前移动3个位置,该调度就变为: S2:r2(A);r1(B);w2(A);r2(B);r3(A);w1(B);w3(A);w2(B) 在该调度中可以找到相邻的冲突操作有r2(B)和w1(B),w2(A)和r2(A),w1(B)和w2(B)。 r2(B)在w1(B)之前,说明T2 图4 调度S2的执行图 图3无环说明调度S1是可串行化的,而且冲突等价于串行调度(T1,T2,T3);图4有环说明调度S2不是冲突可串行化的,因为找不到一个冲突等价的串行化调度[12]。这种执行图判定方法在实现时,需要系统存贮“图”这种复杂的数据结构和便于图节点遍历和回溯访问的索引结构[10],并需要在图的搜索方法中识别“环”,而我们的方法完全基于关系运算的代数方法,直接根据逻辑公式的运算进行判定,简单易行。 事务执行优先关系T1 定义7设F是并发事务集上的执行优先关系集合,T是其中任一个事务,那么(相对于F)事务T的闭包用T+表示,它是一个从F集使用传递推理规则推出的、或为F包含的所有满足T T+={事务A|F⟹T 算法1求事务T相对于执行优先关系集F的闭包T+ 输入:事务T;事务执行优先关系集F 输出:T相对于F的闭包T+ 步骤: {T+:=T; Do { OldT+:=T+; For eachY IfY⊆T+thenT+:=T+∪{Z}; } while(T+≠oldT+); T+:=T+-{T}; Return(T+); } 和函数依赖属性集闭包计算中函数依赖关系[11]不同的是,事务执行优先关系并不具有自反性,即不存在T1 定义8设F是并发事务集上的执行优先关系集合,根据传递推理性规则得到的所有执行优先关系和F自身包含的优先关系构成的全体集合,称为F的闭包,记为F+。形式化表达为: F+=F∪{X 算法2求并发事务集TU的优先执行关系集闭包F+ 输入:并发事务集合TU,事务优先执行关系集F 输出:F+ 步骤: { F+:=∅; For eachT∈TUdo { 调用算法1,计算T+; IfT+≠∅ then { For eachA∈T+do F+:=F+∪{T } } Return(F+); } 例2已知并发事务TU={T1,T2,T3},事务执行优先关系集合F={T1 根据算法2,当T=T1时,调用算法1得到T+={T2,T3},所以F+={T1 根据定义5,如果T1 定义9如果一对事务T1、T2,已知T1 定义10类似(T1 谓词表示个体性质或个体之间的关系,一些更复杂的关系和性质可用多元谓词或谓词与联结词复合形式描述[13]。例如“3小于2”可以表示为:L(3,2)。 定义11[13]原子公式、量词和联结词按照一定规则组成的,用以表示复杂命题的符号串,称为谓词逻辑合适公式,简称为谓词逻辑公式或谓词公式。谓词公式按如下方式生成: (1) 原子公式是谓词公式; (3) 如果A和B是谓词公式,则(A∧B)、(A∨B)、(A→B)、(A↔B)是谓词公式; (4) 如果A是谓词公式,(∀x)A、(∃x)A是谓词公式; (5) 有限次使用(1)、(2)、(3)、(4)后得到的字符串才是谓词公式。 以下定理及证明作为本文提出的判定算法的理论基础,即表明该算法设计的正确性。 定理1若调度S中一对冲突事务 证明:假定T1和T2存在两个可串行化交换方向,T1和T2是可串行化的。不妨设T1和T2的一个可串行化方向为T1 我们的判定方法需完全检测冲突事务集合,在事务集的两两事务检测中累积(T1 定理2冲突事务集 由定理1可知,在调度S中Ti和Tj不可串行化,即调度S没有冲突等价的可串行化调度;反之,若(T1 根据以上定理,我们设计以下算法判定并发事务集TU的调度S是否可串行化。 算法3根据逻辑公式判定并发调度S的可串行性 输入:并发事务集TU和并发调度S 输出:若具有可串行性则返回true,否则返回false Step1根据定义5,得到并发调度S中TU上事务之间的优先执行关系,所有这种优先关系形成集合F; Step2根据算法2,求F+,将事务集TU上事务分配一个识别码Tid,按Tid由小到大排序; Step4将所有谓词按逻辑“与”组合成合取公式: ξ=Small(T1,T2)∧…∧Small(Tm,Tn) 由定理1和定理2的证明可知算法3是正确的,由文献[11]可知改进的闭包计算是可终止的,即算法3是可终止的。 为了验证本文提出算法的实用性和有效性,采用文献[12]中的实例,并用本文算法进行详细分析。 例3如下调度由3个事务T1、T2、T3的动作构成。 S:r2(A);r1(B);w2(A);r3(A);w1(B);w3(A);r2(B);w2(B)。 即有并发事务集TU={T1,T2,T3},按算法3分析如下: 第一步:根据定义5在调度S中可以找到的相邻冲突操作有w2(A)和r3(A),w1(B)和r2(B)。w2(A)在r3(A)前,说明T2 第二步:调用算法2,计算F+。 当T=T1时,T+={T2,T3},F+={T1 当T=T2时,T+={T3},F+={T1 当T=T3时,T+=∅,F+={T1 第三步:根据F+,建立谓词:Small(T1,T2),Small(T1,T3),Small(T2,T3)。 第四步:组成合取公式:ξ=Small(T1,T2)∧Small(T1,T3)∧Small(T2,T3)=true,即TU={T1,T2,T3}的调度S可串行化,该结论与文献[12]中分析结果一致。 例4调度S:r2(A);r1(B);w2(A);r2(B);r3(A);w1(B);w3(A);w2(B)。即有并发事务集TU={T1,T2,T3},按算法3处理如下: 第一步:根据定义5在该调度中可以找到相邻的冲突操作有r2(B)和w1(B)、w2(A)和r2(A)、w1(B)和w2(B)。r2(B)在w1(B)之前,说明T2 第二步:调用算法2,计算F+。 当T=T1时,T+={T2,T3},F+={T1 当T=T2时,T+={T3,T1},F+={T1 当T=T3时,T+=∅,F+={T1 例5考虑下面的调度S:r2(A);w2(A);r3(A);w1(B);w3(A);r2(B);w2(B);r1(A);w1(A)。即有并发事务集TU={T1,T2,T3},按算法3分析如下: 第一步:根据定义5在调度S中可以找到相邻冲突操作有w2(A)和r3(A)、w1(B)和r2(B)、w3(A)和r1(A)。w2(A)在r3(A)之前,则T2 第二步:调用算法2,计算F+。 当T=T1时,T+={T2,T3},F+={T1 当T=T2时,T+={T3,T1},F+={T1 当T=T3时,T+={T1,T2},F+={T1 根据文献[12]可以建立如图5所示的执行图。 图5 例5中调度S的执行图 由于图5中出现了环,可以判断调度S不可串行化,即本文算法3可取得利用文献[12]中执行图判定同样的效果。但本文方法完全是基于关系闭包计算和谓词公式计算的代数方法,算法实现时不用转换为图结构存贮,也无需在图搜索算法中“识别”环。 并发事务可串行化判定是事务并发控制的重要任务之一,现有方法采用执行图判定,具体实现判定功能时需要存贮为图这种复杂数据结构,而且需要用图搜索方法识别“环”的存在。与这种传统的、基于图论的方法不同,本文提出一种基于事务执行优先关系闭包运算和一阶二元谓词逻辑公式计算的代数方法,算法设计逻辑简明,不需要复杂的数据结构和算法流程。通过理论论证和实例分析,验证了本文所提方法的正确性和有效性。未来,将结合并发事务控制中锁机制和基于时间戳的版本控制方法,提出更加有效的并发事务控制方法。

1.3 事务执行优先关系的闭包计算
1.4 谓词逻辑公式


2 本文算法
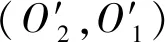



3 实例分析




4 结 语
——论胡好对逻辑谓词的误读
——就Sein论题中实在谓词的理解与胡好商榷

