城市空气污染数据的真实性判别及分析
付 丽 师和欣
(绥化学院信息工程学院 黑龙江绥化 152061)
一、问题的分析
空气中污染物浓度达到有害程度时就构成了空气污染,污染物浓度超过了环境质量标准时,就对人和物造成了危害,它破坏了生态系统和人类正常生活的条件。[1]所有使空气质量变坏的物质都是空气污染物。城市空气污染数据的采集由于各种客观原因,会使采集的数据序列体现出一定的异常现象,因此以部分地区的空气污染问题为背景,然后在现有的国家最新空气污染无监测标准(HJ633-2012环境空气质量指数(AQI)技术规定)的基础上利用异常检测来进行研究。通过建立数学模型,代入相关空气质量和气候的数据,分析空气质量数据是否存在不真实现象,通过污染物之间的相关性来确定数据不真实及严重性,根据已建立的数学模型对数据进行分析,最终为环境保护和政策制定提供支撑。
二、模型建立与分析
我国现在通常采用AQI和空气污染指数(API)来衡量空气质量,根据国家最新空气污染无监测标准(HJ633-2012环境空气质量指数(AQI)技术规定)当中所规定的污染物排放限制,来建立衡量空气质量优良等级的评价模型。
(一)单状态量数据的时间序列自回归模型(autoregressive,AR)。et为服从N(μe,λ2)的正态分布序列,xt为在线监测数据的时间序列,服从N(μ,σ2),其中那么有公式:
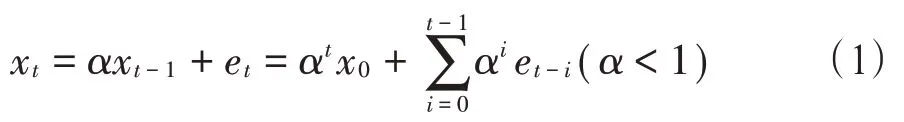
正常状态下每个在线监测状态量,都不应超过相应的限值,那么假设a≤xt≤b。对所有a≤xt+k≤b,可以推导出:
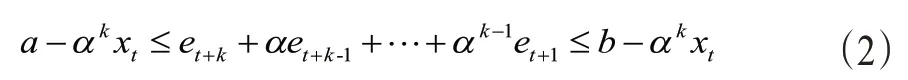
由于et~N(μe,λ2),所以根据(2)可知整个序列满足属于区间[a,b],只能当α小于一个限值α0时才可实现。
因为设备产生故障的过程缓慢,此时监测到的数据通常未超出限值,很难被发现,所以在线监测数据如果没有超出状态量限值时,单纯地用AR模型很难检测出异常状态。
(二)自组织神经网络(self organized maps,SOM)对时间序列的量化。自组织神经网络适用于数据很多、没有标签的状态监测数据。SOM的输入节点为整个序列xt,输出节点为序列c={c1,c2,…,cn},通过公式
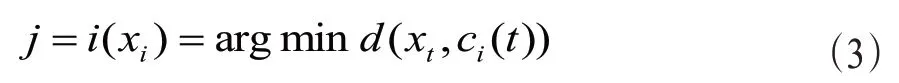
对每一个xt训练其属于节点cj。为确保xt距其所属节点的距离最小,用公式
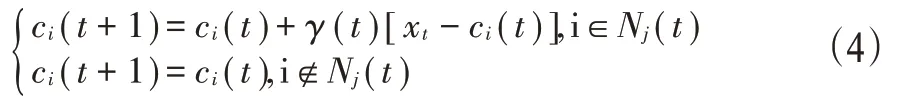
反复进行循环和修正,其中学习速率γ(t)∈[0,1],其随着t的增大而减小。
通过SOM训练完成后,单状态量的时间序列xt就转化为线性空间中的离散点时间序列ct∈{c1,c2,…,cn}:

因为ct表示关于每一个时间点t最接近于xt的节点,所以对时间序列xt的量化就用ct代表了[2]。
(三)时间序列变化过程的挖掘。SOM神经网络的输出节点间通过网络拓扑结构两两相关。在拓扑结构中,由于SOM训练时每个神经元节点与邻域内的节点竞争强,与邻域外的节点竞争弱的这一特点,在拓扑结构中通过量化后的时间序列ct将一个神经元转移到另一个神经元,得出数据随时间的变化规律[2]。
1.神经元所属的概率密度函数。神经元之间的相关关系用一阶转移概率P来表示,AR(n)模型中P[ct+1|c1,c2,…,ct-n+1]为神经元之间的一阶转移概率,可得P[ct+1|ct]为AR(1)模型的一阶转移概率。c1,c2,…,cn取值分别1,2,…,n,在时刻t由式(5)可得,ct=cI的概率为

那么i(xt)的概率密度函数由式(5)和(6)得
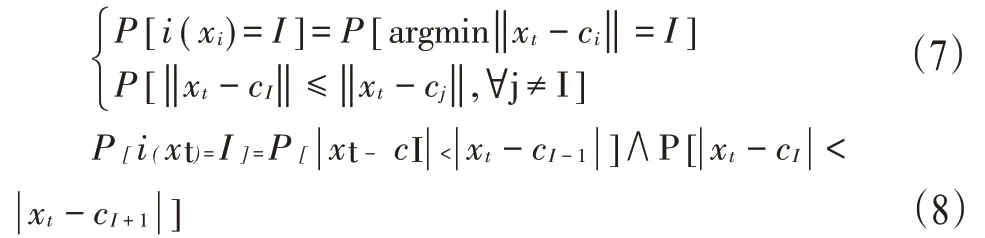
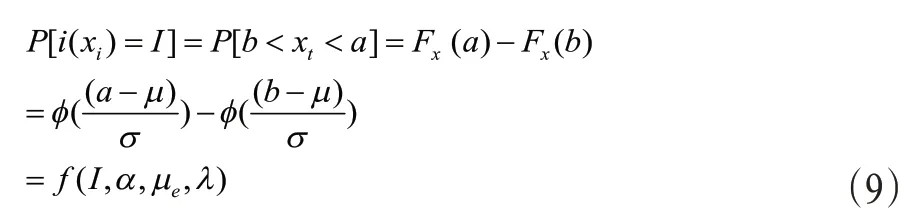
当I=1时,式(9)简化为
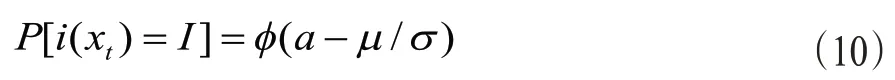
当I=N时,式(9)简化为
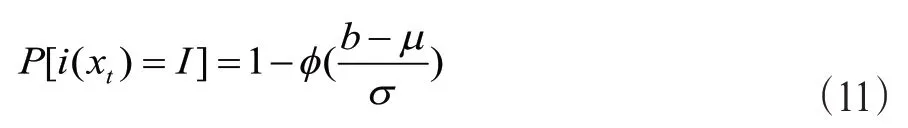
2.神经元之间的转移概率。二阶概率分布函数可表示为
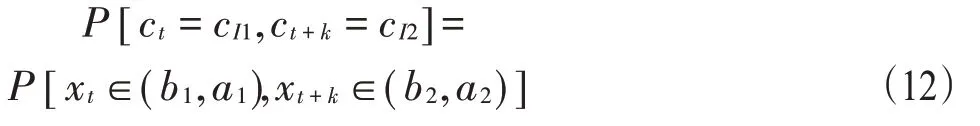
式中cI1,cI2∈{c1,…,cN},I1=(a1,b1),I2=(a2,b2)。由于式(12)中xt属于正态分布,因此xt的二阶正态分布函数为
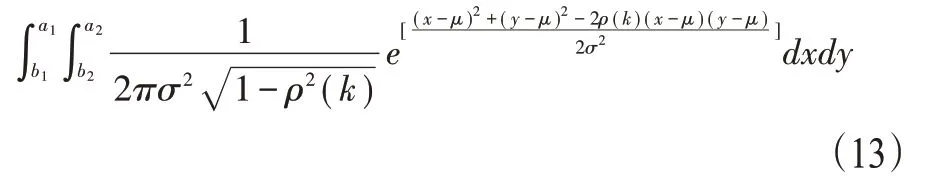
其中一阶AR过程的自相关函数为ρ(k)=αk。由(6)、(9)将(13)式简化为
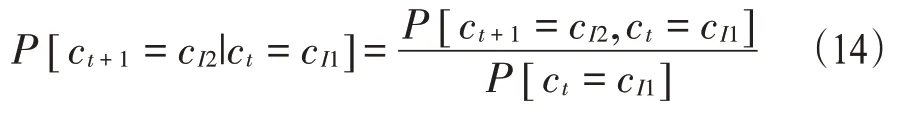
对在线监测数据采用如图1所示步骤,根据时间序列的特征量提取算法进行异常检测。
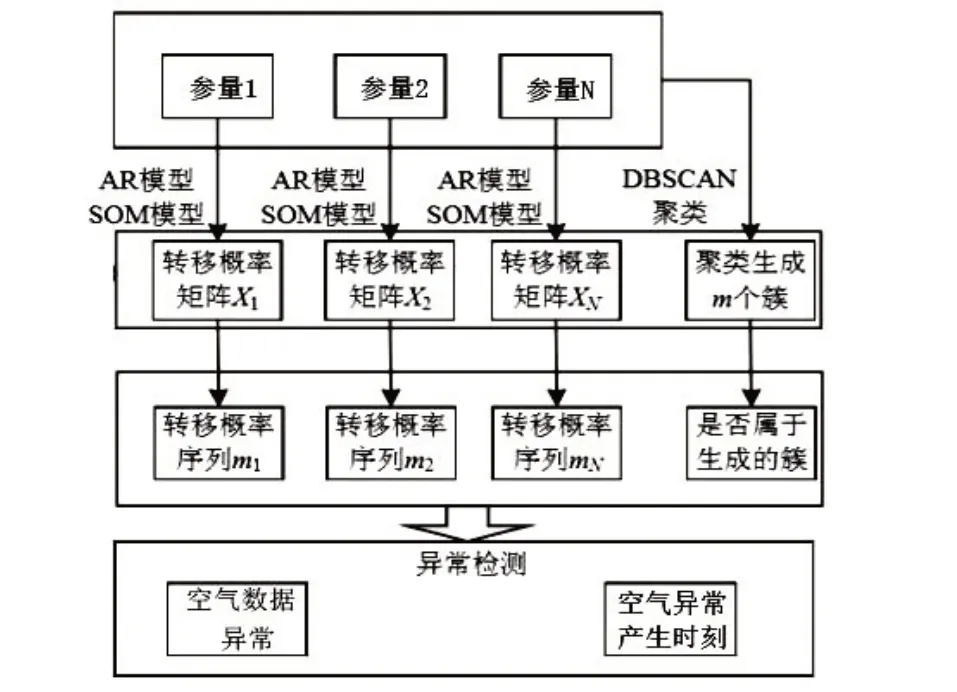
图1 异常检测步骤图
(四)多类Logistic回归分析。我们要引入了多分类Logistic回归模型,因为在实际问题中,响应变量有多种取值,不一定是发生及不发生两种情况。记y是一个响应变量,取值从0到c-1,并且y=0是一个参照组,协变量x=(x1,x2,…,xp),那么可以得条件概率:
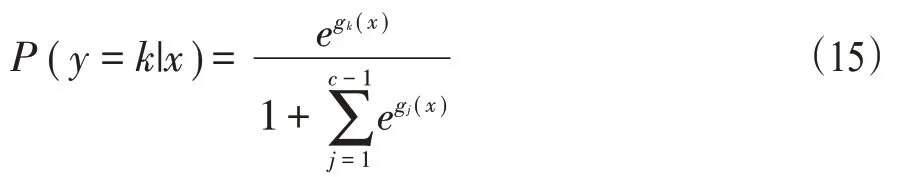
其中k=0,1,2,…,c-1。由此可以得到相应的Logistic回归模型:
显然:g0(x)=0。考虑到社会因素问题,利用线性回归分析建立空气质量和工业生产数据之间的函数关系的数学模型,同时利用其他地区的数据,验证了该模型有效性。线性回归的数学模型为
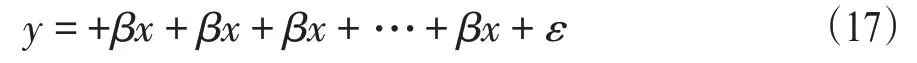
用矩阵形式表示为

其中:y=(y1,y2,…yn)T为解释变量;α=(α1,α2,…αn)T为模型的截距项;
β=(β1,β2,…βn)T为待估计参数;x=(xij)n×k为解释变量;ε=(ε1,ε2,…εn)T为误差项。用α+Xβ组成的线性部分和随机误差项εt解释被解释变量的变化。线性模型估计相关的参数一般采用最小二乘估计法。估计相关的参数是回归分析的核心也是预测的基础。最后根据全国各省上半年PM均值排名及钢材产量分省市统计数据,利用多类Logistic回归分析SSPSS软件获得结果。
三、结语
这个模型充分地考虑到每一个因素所存在的差异,利用模型对城市的空气质量数据进行重新鉴别,增强了数据科学性。模型对各城市空气污染数据采用函数计算的方法来解决问题,依据已查找的数据计算分析AQI,提高了模型准确率。依据原有的数据和已计算出的数据进行对比,更加直观的判断了空气污染数据的真实性。该模型在计算,制定计划,政策分析等领域都可以广泛应用。但是这个模型也有不令人满意的地方,虽然要解决城市的空气污染数据真实性问题,但是受数据的限制,只是判断某些城市的某些天的空气污染数据的真实性,那么位于同一空气质量等级的城市还需要更多的数据,更多的背景加以数学处理和讨论。

