基于改进差分进化算法的曲面零件匹配检测研究

(1.中国船舶重工集团公司第七一八研究所，河北 邯郸 056000； 2.华中科技大学 机械科学与工程学院，湖北 武汉 430074)

图像匹配技术又称图像配准、图像对齐技术，其在复杂零件的加工、检测、逆向工程、图像处理以及模式识别等领域有着重要的应用[1-4]。图像匹配技术以三维点集为研究对象，通过刚体转换矩阵把处在不同坐标系中的两片或多片点集匹配到同一坐标系内，并使对齐误差最小。

匹配技术最早是在70年代美国军事研究中提出的。20世纪80年代后，不同领域的学者对数据匹配进行了深入研究，提出了许多改进方法并得到了广泛的应用[5-6]。目前，应用最为广泛的匹配算法是1992年Bsel等人提出的ICP(Iterative Closest Point)算法[7]，该算法通过计算两片点集中对应点的距离，能够快速找到一个合适的刚体变换矩阵，使得点对间的距离和最小。但ICP算法对待匹配的两片点云的初始位置有特定要求。此外，由于该算法以最小二乘法来求解变换矩阵，对于一些复杂的点云数据，该算法的求解结果易陷入局部最优。因此，近几年不少学者对ICP算法的收敛速度和收敛性进行了较多研究[8-10]。

随着计算机技术的发展，启发式算法的研究取得了巨大的成就，其良好的寻优能力及收敛性能在三维点云匹配研究领域也得到了广泛的应用。Lee[11]等人采用遗传编程算法删除深度图像匹配过程中的异常点； Cai[12]等人利用分支定界方法来解决LiDAR扫描图像的匹配问题；Casella[13]等人提出一种自适应分布式差分进化算法来解决深度图像的匹配问题并利用GPUs来加速计算过程；Corden[14-16]等人利用多种智能算法解决图像匹配问题，尤其在医学图像处理领域取得了较大的进展。

本文利用改进的差分进化算法解决曲面零件匹配检测问题，通过种群进化来搜索最优的旋转和平移矩阵。本算法对点集的初始位置不敏感，能够有效解决ICP算法易陷入局部最优的问题。此外，该算法收敛速度快、鲁棒性好，在曲面零件加工及检测环节能够有效降低测量误差对尺寸检测及加工余量检测的影响，满足生产节拍要求。

1 点云匹配模型

所研究的图像是深度图像，即通过非接触式光学扫描仪获得的图像。相比较于传统的接触式三坐标测量仪，非接触式扫描仪具有测量速度快、对工件材质无要求以及测量视角广等优点。三维图像匹配框架如图1所示，从图中可以看出，匹配的几个关键步骤主要包括：点集输入、计算转换矩阵、模型位置更新及误差判定。

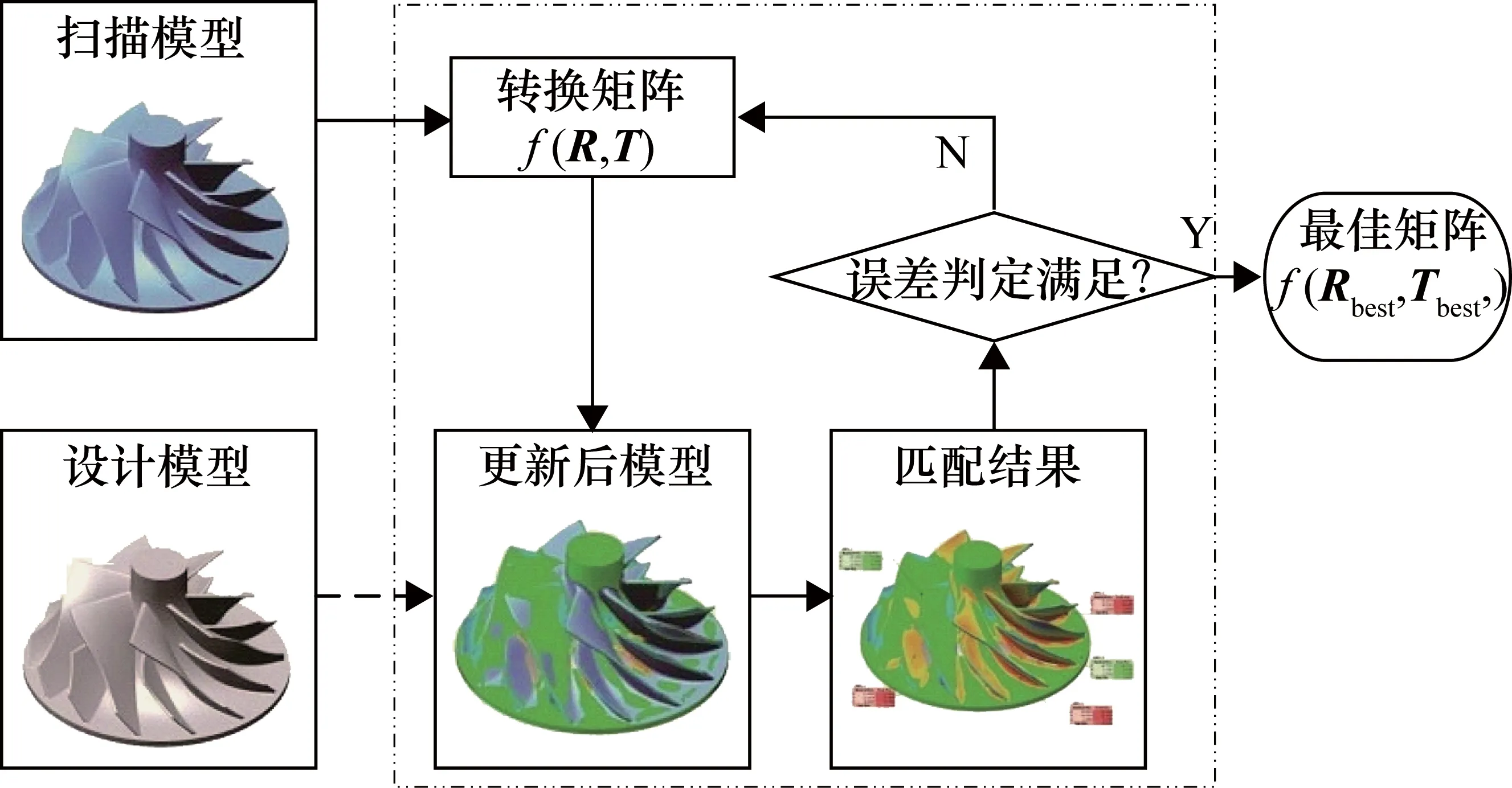
图1 匹配检测流程图

假定工件在设计坐标系下的模型点集为Q，Q={qi}，i=1,…,nq。其中，nq为设计点集中点的个数；工件扫描坐标系下模型点集为P，P={pi}，i=1,…,np，其中，np为扫描点集中点的个数，np=nq。式(1)表示对P中的点进行旋转和平移操作。

f(pi)=R(pi)+T，i={1,…,np}

(1)

式中，R为对点集中的一点执行旋转操作；T为对点集中的一点执行平移操作。现使设计坐标系下的点集Q保持不动，通过对点集P中的所有点执行旋转和平移操作，使得两片点集中的对应点进行匹配。该操作的目标是找到一个最优的变换矩阵f*，使得变换后，两片点集间的各点距离和最小，如式(2)所示。

(2)

经相似度测量，使得式(3)中的F值最小。

(3)

由于实际中较难获得两片点云间精确的对应关系，一般采用增加点数来提高变换矩阵的计算精度。在ICP及其相关的改进算法中，对于旋转矩阵R和平移矩阵T的求解，目前采用最多的是奇异值分解法。这种方法需要计算点集的重心，并构造协方差矩阵，通过求取最大特征值或最大特征向量首先解得旋转矩阵R，并根据式(4)求得平移矩阵。

T=μQ-RμP

(4)

式中，μQ、μP分别为Q、P点集的重心。

2 改进差分进化算法

差分进化算法(Differential Evolution,DE)[17]是一种并行搜索方法，常用于求解非线性连续空间函数的优化问题。DE算法通过个体的选择、交叉和变异过程进行种群的更新。

2.1 算法编码

利用改进的差分进化算法解决点云匹配检测问题，并把需要求解的3个旋转变量和3个平移变量定义为种群个体，如式(5)所示。

(5)

式中，Np为种群大小；txi、tyi、tzi分别为沿x、y、z轴的平移量；rxi、ryi、rzi分别为沿x、y、z轴的旋转量。其中，对于各平移变量的正负值表示沿各坐标轴的正负方向；对于各旋转变量的正值表示绕各坐标轴顺时针方向旋转，负值表示绕各坐标轴逆时针方向旋转。

2.2 变异策略

差分进化算法在种群进化过程中有多个变异策略可选，当用于解决匹配问题时，复杂的变异策略将降低算法的计算效率。基于点云匹配问题的特性，在可接受的计算精度范围内设计了一种新的变异策略。 “DE/rand/2/bin” 策略是根据随机选择的5个个体进行种群的更新，具有较好的全局搜索能力。“DE/best/2/bin” 策略生成新的个体时是根据当前最好的个体来生成的，该策略具有较强的局部搜索能力。本文结合这两种策略的优势，设计了一种新差分进化算法，简称FDE。根据每个个体计算得到的适应度值，把个体分为“good”个体和“bad”个体。其中，对于“bad”个体采用“DE/rand/2/bin”策略进行变异，对于“good”个体采用 “DE/best/2/bin”策略来进行变异，该混合策略能够显著提高算法的可靠性。定义分类因子为λ,且λ∈(0,1)，“good”个体和“bad”个体的种群数量采用式(6)进行计算。

(6)

式中，round( )为随机操作，种群个体按式(7)和式(8)进行更新。

vbad,i,G=xr1,G+F·(xr2,G-xr3,G)+F·(xr4,G-xr5,G)

(7)

vgood,j,G=xbest,G+F·(xr6,G-xr7,G)+F·(xr8,G-xr9,G)

(8)

式中，i∈[1,NPbad]；r1～r5为在[1,NPbad]区间内随机选择的个体且不等于i；j∈[1,NPgood]；r6～r9是在[1,NPgood] 范围内随机选择的个体，且不等于j；xbest,G为当前种群内的最好个体。本文中，比例因子的选择方法为[18]

(9)

式中，F0为个常量；Gmax为最大迭代次数；G为当前进化次数，且G=1,2,…,Gmax。

3 实验及结果分析

如图2所示，采用5个复杂曲面零件模型进行试验。从左到右，从上到下依次为叶片1、叶片2、法兰、汽车，以及气道模型。针对每个模型的扫描点云采用均匀法进行采样，采样个数为1000。

为验证本文所提算法对复杂初始位置的有效性，和文献[19]的试验方法一样，本文利用扫描模型经一定空间变换T转换后再对齐到其原始扫描模型。为增加模型初始位置的复杂性，按表1设置了3个初始位置，表中，L为模型空间尺寸(长、宽、高)的最大值。

表1 预设转换矩阵

为验证本文方法的鲁棒性，在转换后的模型上增加了20个噪声点，并将本文所提方法与 ICP[7]、SICP[20]、IRLS[21]、ADF[19]、DE等5种方法进行了对比。在ICP、SICP、IRLS和ADF算法中最大迭代次数设置为50。结合本文问题的计算效率要求，算法的最大函数评价次数设置为30000。对于DE和FDE个体数量设置为50，最大迭代次数为Itermax=6000。经定量比较的匹配结果如表2所示。表中加粗数据表示计算结果的最优值。

从表2可以看出，对于本文采用的5个曲面零件模型，ICP和SICP算法随着模型初始位置复杂程度的提高，其计算误差逐渐增大。对于叶片2模型，在T1和T2位置情形下ICP、IRLS和FDE算法均能获得全

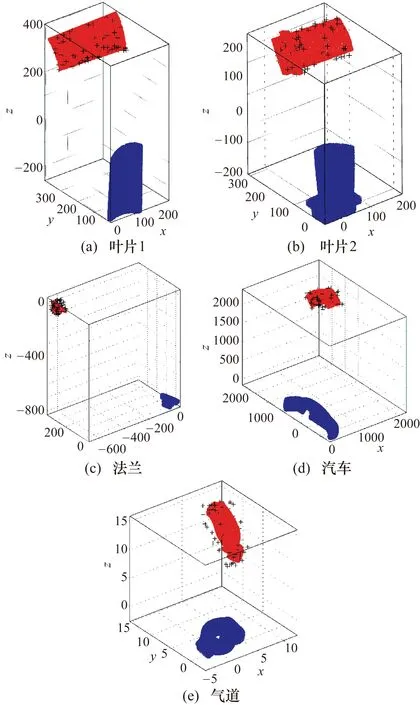
图2 各模型初始位置图

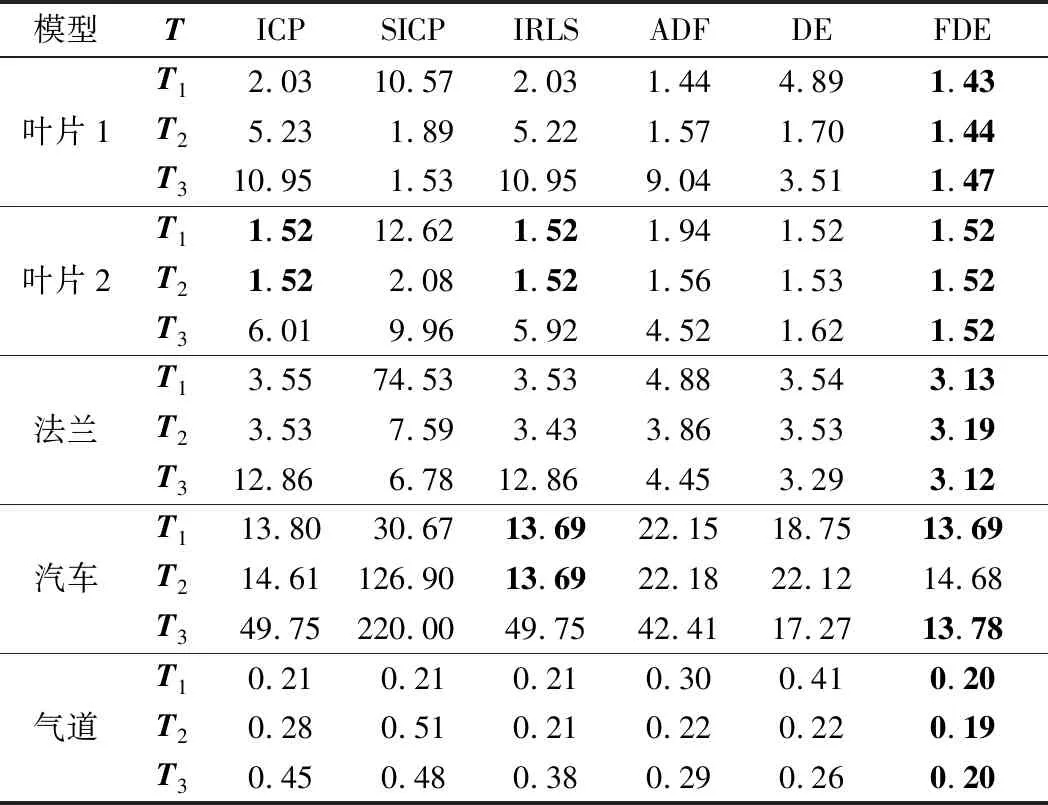
单位：mm

局最优解。但在T3位置情形下，前两种方法由于搜索能力有限其计算结果已陷入局部最优，而FDE算法对模型的初始位置不敏感，在较复杂的T3情形下仍能保持较强的全局搜索能力。相对来说，ADF算法采用自适应计算策略其结果要优于ICP、SICP、IRLS和DE算法，但由于ADF本质上仍属于确定性算法，其全局搜索能力有限。通过以上对比发现，所提出的FDE算法在计算精度、搜索能力以及鲁棒性等方面均优于其他5种方法。

图3～图7为各算法在T3初始位置时所计算得到的匹配结果，其中各图(a)～图(f)依次为ICP、SICP、IRLS、ADF、DE、FDE算法的匹配结果。

图3～图7定性比较了各算法在T3位置情形下的匹配结果。从这些匹配结果中可以看出，ICP算法对叶片1和法兰模型的匹配结果误差较大，经空间转换后待匹配的两模型仍存在明显的位置偏差。SICP算法虽在叶片1模型获得较好的匹配结果，但对于汽车模型该算法计算结果误差较大，算法通用性差。在该对比条件下，ADF算法计算结果优于IRLS算法，但这两种方法易受噪声点的影响，计算结果为局部最优解。启发式算法DE和FDE采用随机搜索机制具有较强的全局搜索能力，在该对比条件下两者的计算结果明显优于其他4种算法。但是，DE算法所得结果在模型边界处的匹配误差较大，相比较来说，FDE算法所得结果更优。

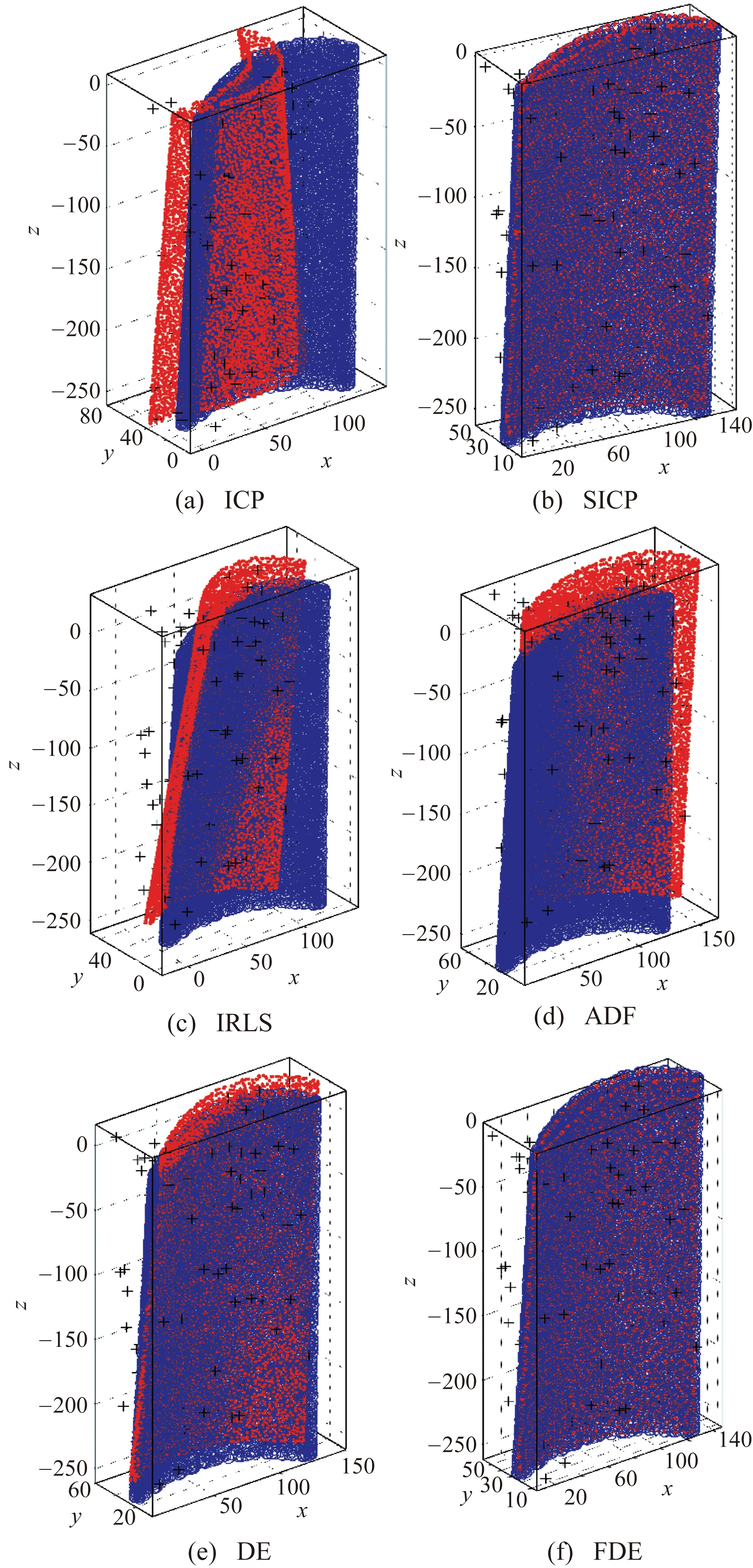
图3 叶片1模型匹配结果

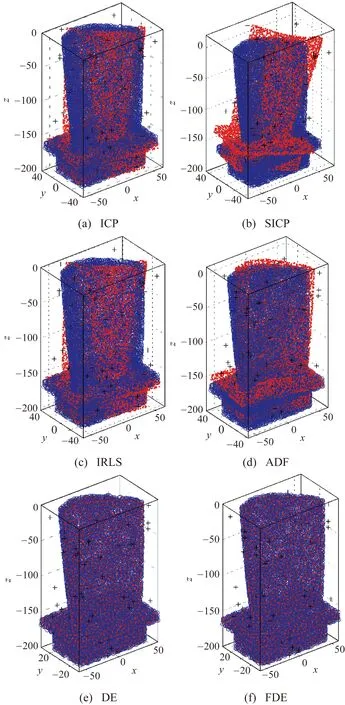
图4 叶片2模型匹配结果

图5 法兰模型匹配结果

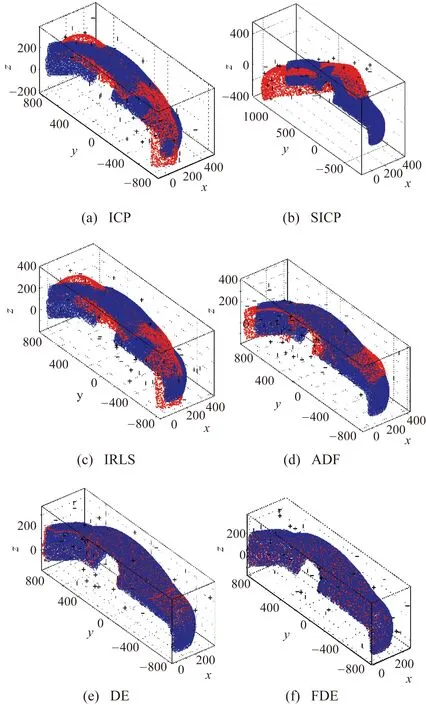
图6 汽车模型匹配结果

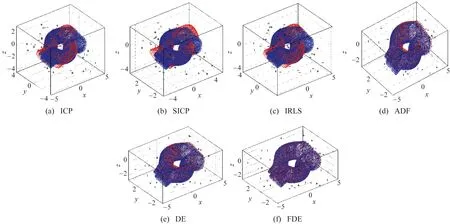
图7 气道模型匹配结果

4 结束语

本文针对复杂曲面零件的结构特性，利用改进的差分进化算法求解模型匹配问题，有效解决了曲面零件的质量检测中匹配误差对检测精度的影响问题。通过对算法种群编码方式、个体变异策略的选择等方面的深入分析与改进，大大提高了个体的寻优能力。本文所提方法可有效解决ICP算法易陷入局部最优的问题，且本方法对点集的初始位置不敏感，算法收敛速度快、鲁棒性好。本文算法所得结果能够保证为全局最优解，为复杂曲面零件的质量检测提供可靠的精度保障。