海上施工水域船舶航线规划数学建模及求解

谢新连，刘 毅，何 傲

(大连海事大学 交通运输工程学院 , 辽宁 大连 116026)

0 引 言

水上施工会给通行船舶带来许多限制和安全风险，海上施工水域往往也是交通事故的高发区域。当施工环境比较复杂、通航限制较多时，船舶安全航线的设计就显得格外重要，也具有难度。特殊水域上船舶航线自动规划的发展将很大程度决定现代无人驾驶船舶技术的发展水平。早在现代智能化无人船出现之前，路径规划已经有大量的相关研究[1]

传统的船舶航线规划是指在静态和动态障碍物并存的环境中，寻找一条从已知起点到终点的满足一定评价标准的航行路径，使得船舶在航行过程中能够安全可靠地避开所有的障碍物[2]。常见的航线规划方法有动态规划法、最速下降法、最优控制法、启发式搜索法、神经网络法、模拟退火法、遗传算法等。由于每种航线规划算法都或多或少存在一些缺陷，所以实际应用的方法大多数是基本算法的改进算法，或者融合了数种基本航线规划算法的算法[3]。孟祥杜[4]做了无人船路径规划算法研究，针对无人船工作水域具有不规则边界且常常存在障碍物的特点，也介绍了几种常用的建立环境模型的方法。

环境建模也是智能驾驶技术研究最基本、最关键的环节之一，在环境建模方面的研究，王飞等[5-7]采用栅格法进行环境建模，提出了基于Maklink图和遗传算法的改航路径规划方法，并且利用遗传算法对Maklink图中的初始飞行器航线进行了改航规划；李明富等[8]在Maklink图的基础上采用变参数萤火虫算法对路径进行优化，实验表明改进后的萤火虫算法能够较好的解决离散路径规划问题；孟祥杜[4]做了无人船路径规划算法研究，针对无人船工作水域具有不规则边界且常常存在障碍物的特点，也介绍了几种常用的建立环境模型的方法。

由以上的文献可以发现，目前研究的问题主要集中在普通或正常环境下各种交通工具的路径的规划。然而在特殊环境下的路径规划研究则较为罕见。而且船舶的路径规划和航线设计有其自身的特殊性，船舶在水中的操作性能和陆上的交通工具或机器人也有较大差异，因此不能生搬硬套其它交通工具的路径规划的方法。船舶在海上航行时事故频发的区域就是海上的施工区域，海上施工种类繁多，对其附近船舶的影响也各不相同，为了保证船舶能够顺利的通过施工水域，有必要对施工水域的船舶航线规划进行相关的研究。

1 问题描述及环境模型的构建

船舶在海上航行时可能会经过某些施工水域，并且在有的水域中同时包含多个水面和水下施工地点，当在同一片施工水域中包含多个施工点时，船舶在其中的航行将变得极为复杂和危险，假设船舶在某施工水域中的环境示意如图1。

图1中，S为航线规划的起点，T为航线规划的终点，其中的阴影部分表示海上的施工区域。

为了方便施工水域的航线规划数学模型的建立，首先利用Maklink图论的方法来处理施工水域的危险区域，通过在施工水域中构造Maklink链接图来构造施工水域中的可航行网络图，构造Maklink航线网络图的具体步骤可以参考文献[5, 8]。由于船舶始终是处于海平面高度，因此笔者建立数学模型时不考虑海拔高度的影响，将环境模型的构建简化为二维平面。另外对施工水域中所有的不可航行区域都采用凸多边形或多个凸多边形的组合来表示。在模型化表示不可航行区域的基础上进一步构造可航行的自由空间，海上施工水域的可航行自由空间是由链接线构成的凸多边形。在图1的环境模型中构造的可航行自由空间如图2。

图1 施工水域环境示意Fig. 1 Schematic diagram for construction waters

图2 可航行自由空间Fig. 2 Nautical free space map

构造可自由航行空间图时主要需要遵循以下两个基本准则：①所构造的链接线不能够穿越施工水域中的危险区域；②链接线的一端是施工水域的危险区域所构成的凸多边形的顶点，另一端是另一个施工危险区域构成的凸多边形的顶点或者是施工水域的自由空间的边界点。

在施工水域的自由空间中，将所有链接线的中点两两相连所形成的图就是需要构造的可航行区域的Maklink航线网络图，如图3。

图3 施工水域的MaklinkFig. 3 Maklink diagram for construction waters

2 海上施工水域航线规划的数学模型

将图3中构造的Maklink航线图，进一步表述为可求解的数学模型。假设由起点S到终点T的一条在施工水域中的航线是由点序列(S,p1,p2,…,pk,T)组成，数学建模时其目标方程就是点序列所构成的航线的距离最短。在点序列中，船舶在除了起点S和终点T以外的所有中间点处都有可能转向，为此我们需要考虑转向角对船舶航行的约束，船舶在一定的航行速度下，船舶在pi处的转向角我们用θpi来表示，它不能超过其转向角的极限角度，用φmax表示船舶在设计航速下的转向极限角度。另一方面船舶的转弯半径也是航线设计中必须考虑的一个重要因素，船舶转弯的转弯半径和船舶所处的航行速度有很大的关系，根据参考文献[9-10]中指出船舶在没有拖轮的辅助的情况下在10 kn的设计航速下船舶的最小转弯半径可按表1 的设计参数选取。

表1 航道转弯半径设计指标Table 1 Channelturning radius design index

根据十一五科技攻关项目“沿海深水港航道选线及设计主要研究”中[11]，对10万吨级集装箱船、15万吨集装箱船和10万吨级LNG船舶在不同转向和航速情况下的转弯进行的模拟研究，得出了航道的转弯半径R也可按照公式(1)估算：

(1)

式中：R为航道设计的转弯半径,m；Vt为航道的设计行驶速度，kn;L为航道的通行船长,m；θ为船舶在某点需要转向的角度,(°)。

研究发现航道的转向角达到60°时，船舶的操纵出现操纵困难的现象，船舶操纵人员不易掌握船位、转向角速率及在航道上的姿态；当转向角达到90°时，操纵极为困难，对操作人员的压力极大，特别是在风、浪、流等自然因素的共同作用下，过弯操作的失误率明显增加[12]。因此在进行航线规划时，得到的航线必须满足船舶在设计航速下在各个转向点处的转向角度小于等于90°。

考虑这些因素后，建立船舶在海上施工水域中航线规划的数学模型如式(2)～式(6)。

(2)

s.t.

∀l(pi，pi+1)∩Sj=∅,i=1,2,3,…,n,j=1,2,3,…,m

(3)

∀θPj∈(1,…,k)≤φmax

(4)

RPj∈(1,.…,k)≥λL

(5)

D≥Dmin

(6)

模型的解释：公式(2)表示目标方程，其中(pi,pi+1)表示由pi和pi+1两点构成的航段，d(pi,pi+1)表示航段(pi,pi+1)间的距离，式中k表示路径终点T前的最后一个节点。目标方程由三部分组成，第一部分表示组成航线的中间航段的长度总和，后面两部分表示连接起点和终点的航段长度。公式(3)表示构成航线的任意航段与施工水域的危险区域的交集为空集，其中l(pi,pi+1)表示由pi和pi+1两点连接形成的航段的点集；Sj表示施工水域中危险区域的点集。公式(4)表示船舶在第pj节点处的转向角必须小于航线设计航速下船舶的最大安全转向角φmax，由前面的研究结果可知一般情况下φmax≤90°。公式(5)表示的是在pj节点处船舶进行转向时，航线必须满足船舶最小转弯半径的要求，其中L表示船舶的长度,m；λ表示航道在不同设计航速下所取的最小转弯半径与船长的比值。公式(6)表示规划航线与危险区域的最小距离的约束；D表示航线某处与危险区域的最小距离；Dmin表示船舶与危险区域的最小安全距离,m。

3 Dijkstra算法求解航线规划数学模型

对建立的数学模型的求解，采用两阶段优化求解的方法：第一阶段采用Dijkstra算法，在建立的Maklink可航行航线网上搜寻经过网络节点的最短航线；第二阶段再利用蚁群算法对得到的初始解优化，最终得到最优的航线。

Dijkstra算法是用于解决非负权值网络中寻找指定两点间最短距离的最好的算法之一。Dijkstra算法的基本思想是采用标号法，给每个节点预先设置两个标签，其中一个用于标记路长，另一个是用于标记从起点到终点路径的最后一条弧的起始点号。网络节点的标号分为两类，一类是永久标号，另一类是临时标号。当迭代至第k步时，获得永久标号的点意味着已经找到起点到该点的最短路径，将获得永久标号的点放在Sk集合中，获得永久标号的点的路长d值和路径标号ξ值不再修改。

在利用Dijkstra算法求解前，需要得到Maklink图中网路节点各点间的邻接距离矩阵，航线网络图的邻接距离矩阵为一个19×19阶的矩阵，即：

在邻接距离矩阵中，∞表示两个节点不连通，其距离为无穷大，其中的数字25则表示p1和p3是连通的，并且两点间的距离为25 km。利用Dijkstra算法求解得到的结果的总距离为221.573 0 km，其路径依次为S-p8-p9-p2-p1-p12-p13-T。航线规划的结果如图4。

图4 Dijkstra算法求解路径Fig. 4 Diagram for Dijkstra algorithm solution

4 蚁群算法对初始航线的优化

在构造海上施工水域中的航线图时，选择的是可自由航行链接线的中点来构造Maklink航线网络的节点，但是根据模型约束条件式(6)的实际要求，只要与施工水域中的危险区域的距离大于Dmin即可自由航行，因此最优的航线不一定经过航线的网络的中点。即节点pi的位置是可以在自由空间的链接线上进一步优化的，因此下面就使用蚁群算法对初始航线进行进一步的优化。

4.1 工作空间离散化处理

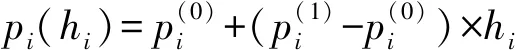
(7)

式中：pi(hi)为链接线上的任意一点；hi为一个0到1的随机数，用它来表示当前点所处在两端点间的比例参数；N为某链路所经过的节点的个数[13]。

在得到Dijkstra算法的解的基础上，只要给出一组(h1,h2，…,hN)参数，就可以得到一组由起点到终点的新解。在采用蚁群算法优化施工水域的船舶航线前，需要离散化工作空间，对链接线的划分笔者采用固定长度划分法。为了满足模型约束条件距离危险区域的最小距离为Dmin的要求，采用的划分长度ξ取Dmin，每条链接线L将划分成的分数为

(8)

式中：Int()函数表示取整函数，当Int(Li/Dmin)为奇数时，为了保证链接线的中点也是一个等分点，将划分的等分数加1，经过离散处理后那么从链接线Li-1到其相邻的链接线Li将会有Ni+1条路径可以选择。

4.2 蚂蚁路径的搜索和信息素的更新

每一只蚂蚁在完成从起点到终点的路径搜索后都会产生一组与之相对应的路径参数集合(h1，h2，…，hk)，在移动的过程中，一只蚂蚁在链接线Li上时，选择下一个链接线Li+1上的节点j的方法为，依次计算当前链接线节点i到下一条链接线节点j的选择概率Pij，然后根据选择概率Pij采用轮盘赌法找出下一个节点j，Pij的计算公式为[14]

(9)

式中：ηi,j为启发值；τi,j为信息素，信息素的浓度越高，选择概率Pij越大。当蚂蚁在移动过程中选择了某个节点，则在该节点处需要释放信息素，则对该节点的信息素需要进行更新的公式为

τi,j=(1-ρ1)×τi,j+τ0

(10)

式中：τ0为信息素的初始值；ρ1为[0,1]区间的可调参数，文中ρ1取0.1。当所有的蚂蚁都完成一次搜索，保存最短路径的长度，同时再次更新每个点上的信息素。此次更新称为信息素的挥发更新，信息素挥发的公式为

τi,j=τi,j(1-ρ2)

(11)

式中：ρ2为信息素挥发参数，文中ρ2的值取0.003。

4.3 蚁群算法对航线转向角的优化

图5 转向角优化示意Fig. 5 Diagram for steering angle optimization

τi,j=λij×[(1-ρ1)×τi, j+τ0]

(12)

(13)

公式(12)为修正后的信息素更新公式，式中λij为新引进的信息素更新公式的修正系数；公式(13)为信息素的修正系数的计算公式，其中αij为当前位置和备选位置的连续与起点和终点位置连线的夹角，为了消除角度正负方向的影响，公式(13)中对夹角 取绝对值。另一方面因为船舶的最大安全转向角度为90°，所以取π/2为参考基准，当αij绝对值大于90°时修正系数λij的值将小于1，将会使路径所含有信息素浓度τi,j减少，从而达到迭代过程选中转向角大于90°的概率不断减小的目标。同时当夹角αij的绝对值越小时λij的值也将越大，当αij的绝对值取最小值0时，λij取得最大值2。

4.4 蚁群算法优化求解最终结果

在利用蚁群算法进行优化求解时，每次迭代产生10只蚂蚁来搜索最优路径，在每一次迭代结束后都记录下这10只蚂蚁寻找到的最优路径和最优路径的长度，总共进行了500次迭代。最终通过蚁群算法求解的航线总长度为205.43 km，比Dijkstra算法求解的路径总长度221.573 0 km减少了16.139 3 km，较初始解缩短了7.87%，最终的航线规划结果如图6。

图6 蚁群算法最终结果Fig. 6 Final result for ant colony algorithm

图6中虚线就是由蚁群算法求得的航线，它不仅在总距离上和初始解相比减少了7.87%，而且航线在转向次数和转向角上也得到了优化。为了满足数学模型约束条件公式(6)的约束，观察图6可以发现蚁群算法优化得到的船舶航线与施工水域的危险水域都保持了一定安全距离，特别是图中的A、B两个地方，船舶航线与施工水域的危险区域的距离已经是算法设置的极限安全距离Dmin，本算法实验中Dmin取值为0.2 km。

为了观察蚁群算法在搜索最优航线时的收敛过程，图7是蚁群算法优化初始解的收敛过程。

图7 蚁群算法收敛过程Fig. 7 Ant colony algorithm convergence process

观察图7可以发现蚁群算法在迭代的初期航线总长度迅速收敛，当迭代100次以后算法收敛趋于平稳，说明此时已经得到了较为优秀的满意解，但是为了减小陷入局部最优解的概率，提升算法搜索全局最优解的能力,可以发现蚁群算法在迭代的中后期出现了几次明显的波动。这是因为在利用蚁群算法求解模型时，蚂蚁种群始终会以一个较小的概率去探索未知的领域，以便于发现全局最优解。

5 结 论

1)为了解决船舶在施工水域中的船舶航线规划问题，以图论的相关理论为基础，在海上施工水域中构建起了可自由航行网络图，利用Dijkstra算法求得了航线的初始可行解。

2)在得到初始可行解的基础上，利用蚁群算法对初始解进行了智能优化，使最终得到的海上施工水域的船舶航线得到了较大幅度的优化。

3)通过两阶段的优化求解求得了既满足航线尽可能短又能够避开海上施工水域危险区域的航线。