基于尺寸效应的钢筋混凝土梁剪切强度研究进展

罗 林，周胤呈，向 博，龚 拯

(1. 重庆交通大学 省部共建山区桥梁与隧道工程国家重点实验室培育基地，重庆400074；2. 重庆交通大学 土木工程学院，重庆400074)

0 引 言

钢筋混凝土梁是由钢筋和混凝土组成的复杂构件，是土木工程结构最常见的受剪构件之一。在荷载作用下，钢筋混凝土梁会发生破坏，主要包括在弯矩作用下的正截面受弯破坏和在剪力、弯矩的共同作用下的斜截面剪切破坏。其中，剪切破坏为脆性破坏，其设计要求更为严格，如框架结构设计准则“强剪弱弯”(即剪切破坏不能先于弯曲破坏)，就体现出设计中为避免出现剪切失效的思路。

从加载到破坏，从微裂纹产生到宏观裂纹出现直至最后贯通破坏的整个过程，钢筋混凝土梁在不断地进行应力重新分布，因而剪切破坏力学机理比较复杂。钢筋混凝土梁剪切破坏机理复杂，也体现在各国设计规范对剪切强度公式描述的差异性上。如中国混凝土结构设计规范：GB50010—2010[1]、美国混凝土规范ACI318-14[2]、欧洲混凝土规范EN 1992-1-1[3]和加拿大混凝土规范CSA A23.3[4]中关于钢筋混凝土梁剪切强度计算理论各不相同。对此，袁健等[5-6]、王峥等[7]分别通过线性拟合收集的无腹筋梁、有腹筋梁剪切试验数据较为详细地分析了各国规范之间差异，并着重论述了我国混凝土规范优点与不足。总体而言，我国房建和桥梁等土建结构设计规范安全设置水准要比国外同类规范低，规范更新修正也相对较慢。随着结构件尺寸增大，安全性将会进一步降低。

此外，随着人类对大自然改造步伐加速，土木工程结构(含地上结构和地下结构)的高度和跨度在不断增大，因而对大尺寸钢筋混凝土梁设计理论提出了更高要求。传统的钢筋混凝土梁剪切强度设计理论和方法及其相应的尺寸效应研究成果都是依据和参考小尺寸梁的试验结果，因而对大尺寸钢筋混凝土梁剪切强度设计缺乏科学依据，也难以保证其可靠度。从各国剪切强度规范可看出，尺寸效应的影响还未达成一致，故将尺寸效应合理纳入规范、修正钢筋混凝土梁剪切强度公式亟需解决。国内外学者对钢筋混凝土梁剪切强度的进行了研究，并取得了重要的成果。

1 理论研究

钢筋混凝土梁(含无腹筋梁和有腹筋梁)剪切强度理论研究已有长达一个多世纪的历史。目前，主要形成5种理论[8-9]：断裂力学法、极限平衡法、桁架模型法、非线性有限元分析法和统计分析法。这些理论广泛地用于钢筋混凝土梁剪切强度分析中。

随着20世纪美国俄亥俄州空军仓库破坏、2006年加拿大蒙特利尔钢筋混凝土吊桥垮塌等事故发生，钢筋混凝土梁剪切强度尺寸效应现象引起了许多学者的重视和关注。这两起事件主要原因都是在设计规范中没有考虑尺寸效应影响，导致梁的抗剪承载力储备严重不足。回顾尺寸效应研究悠远的发展史，学界形成以下3种主要理论。

1)以W.WEIBULL[10]为代表的强度随机性引起尺寸效应统计理论。该理论采用链的最弱连接模型，基于强度随机分布概念，提出了著名的尺寸效应统计理论。该理论认为：材料强度是随机的，且只要材料中一个小的单元达到了极限强度，结构就会失效。该理论早期应用于疲劳引起的金属结构脆断分析并取得了巨大成功。但钢筋混凝土构件，在长度裂纹稳定扩展过程中，结构内可充分完成应力重新分布，产生一种确定性的尺寸效应。

2)以Z.P.BAŽANT[11]为代表的基于断裂能量释放尺寸效应理论。该理论认为：这类准脆性材料尺寸效应是在达到最大荷载前由一个大裂纹或一个包含有微裂纹的断裂过程区稳定增长引起的，尤其是由大裂纹或微裂纹区发展而产生应力重新分布和贮存能量释放所致，即尺寸效应是由宏观裂纹扩展时应变能耗散引起。

3)以A.CARPINTERI[12-13]为代表的微裂纹或断裂分形特性引起的尺寸效应理论。该理论提出了有关尺寸效应裂纹表面的侵入式分形特性和间隙分形特征。该理论认为：在不同的观察尺度下，裂纹分形上的差异性是材料产生尺寸效应的根源。通过建立材料断裂特性与分形维数之间的数学关系式，确定了基于分形理论基础上的尺寸效应理论。

除这3种主要理论外，还包括：材料非均匀性和泊松效应引起的边界层尺寸效应理论，裂纹尖端三维应力奇异性引起的尺寸效应理论，扩散现象引起的时间相关尺寸效应理论、材料本构关系时间相关性引起的尺寸效应理论[14]。以上4种理论都属间接引起的尺寸效应现象，故笔者在分析过程中主要还是以3大主要理论为基础。

1.1 基于尺寸效应的无腹筋钢筋混凝土梁剪切强度理论研究

1900年以前，学界错误认为无腹筋钢筋混凝土梁剪切破坏是一种纯剪现象。1900年以后，剪切破坏逐渐形成了两种机理：① 继续认为钢筋混凝土梁剪切破坏是一种纯剪现象；② 认为是沿着斜截面的拉裂破坏[15]。

E.MÖRSCH[16]指出：如果钢筋混凝土梁剪切破坏是一种纯剪现象，那么根据材料力学单元体分析，在只存在剪应力的单元体上，45°斜面上肯定存在同等大小拉应力 (图1)。对混凝土而言，其拉伸强度低于剪切强度，故破坏往往会沿着斜截面发生。文献[16]对梁的剪切破坏给出了清晰的认识，但认为钢筋混凝土梁名义剪切强度只与混凝土强度有关，忽略了尺寸效应以及其他因素对无腹筋钢筋混凝土梁剪切强度影响，有一定局限性。

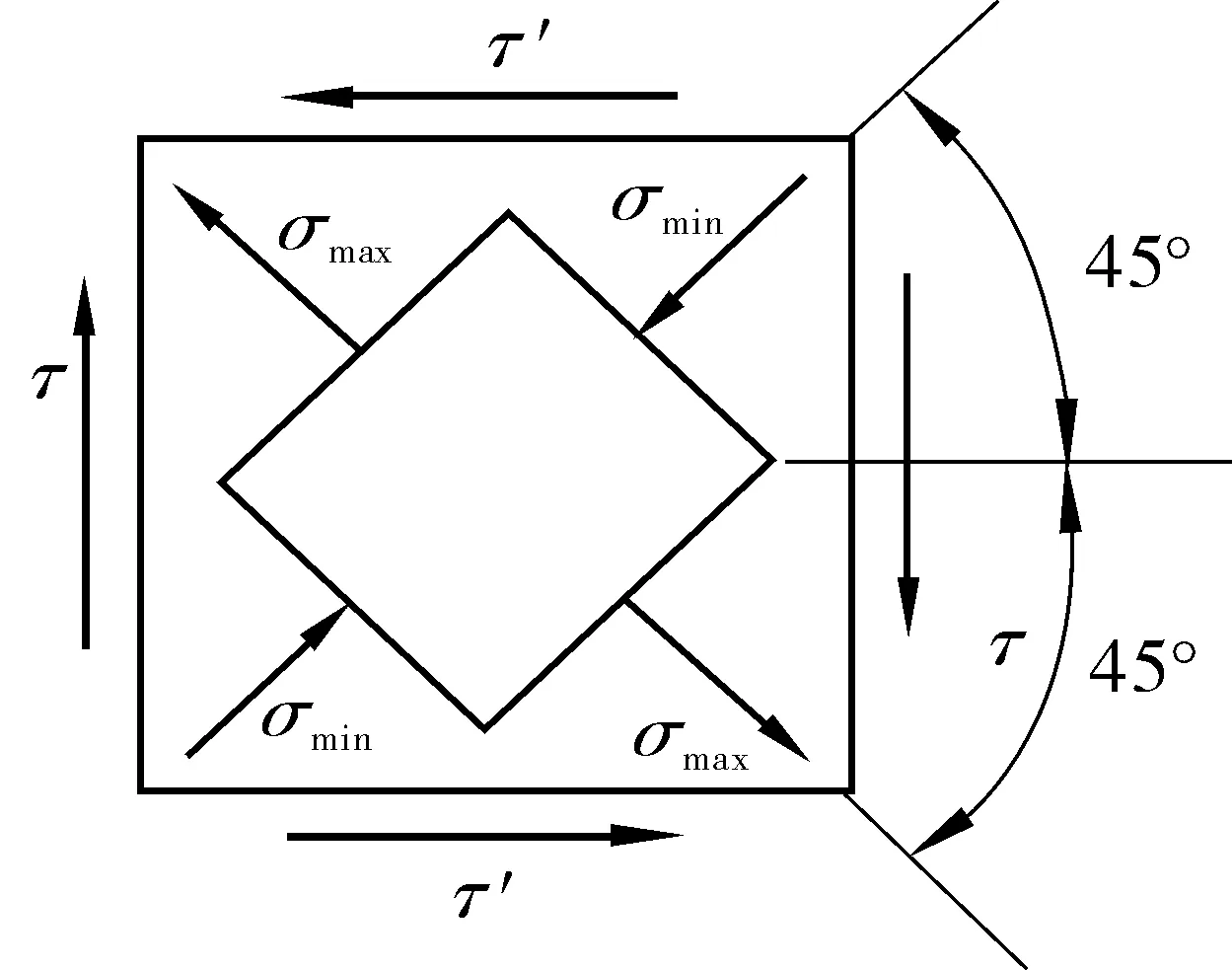
图1 单元体应力状态Fig. 1 Unit body stress state

Z.P.BAŽANT等[17]结合断裂力学原理提出了基于尺寸效应的无腹筋钢筋混凝土梁剪切强度的简单公式，如式(1)：

(1)

式中：vu为实际剪切强度；v0为名义剪切强度；d和da分别为梁的有效高度和骨料尺寸；λ0为经验常数，对于无腹筋钢筋混凝土梁λ0=25。

这是较早时期对无腹筋钢筋混凝土梁剪切强度尺寸效应现象的定量研究。在d→0和d→∞两个极端，式(1)巧妙地接近塑性力学和断裂力学的计算结果。也有学者对vu和d的幂指数大小关系存在争议，如：E.C.BENTZ[18]通过分析24个试验数据而采用d-0.33来表征无腹筋钢筋混凝土梁剪切强度的尺寸效应。图2为不同理论下vu和d的8种尺度律关系及ACI-445F剪切强度数据库[19]，即：① Bažant尺度律：基于断裂力学和能量释放提出；② Bažant扩展尺度律：考虑梁有效高度处于极大和极小尺寸时分别满足脆性断裂力学和塑性力学行为，将尺度律进一步扩展和修订；③ MCFT(modified compression-field theory)即修正压力场理论：尺寸效应由裂纹间距引起；④ CEB-FIP(Comité Euro-International du Béton)公式：由欧洲混凝土协会提出的经验公式；⑤ JSCE(Japan Society of Civil Engineers)公式：由日本土木工程师协会根据Weibull理论建立的尺寸与剪切强度幂指数关系，采用d-1/4来表征无腹筋钢筋混凝土梁剪切强度的尺寸效应；⑥ MFSC多重分形尺度律；⑦ LEFM(Linear Elastic Fracture Mechanics)即线弹性断裂力学，在线弹性断裂力学基础上限定了最大剪切强度；⑧ ACI-445F，由美国混凝土协会于2003年提出的尺度律。

图2 ACI-445F剪切强度数据库及各种尺度律Fig. 2 ACI-445F database for beam shear and plots of various size effect laws

Z.P.BAŽANT等[19]运用量纲分析进一步证实幂指数为-1/2的可靠性，和已有试验数据吻合度也较好，并且将Bažant尺度律运用到无腹筋钢筋混凝土梁剪切强度[19]，如式(2)：

(2)

式中：ρ为纵筋率；f′c为混凝土圆柱体抗压强度；a为剪跨；a/d为剪跨比。

钢筋混凝土梁剪切过程中，伴随着能量吸收和释放。基于文献[11]所提出的能量释放理论，P.J.GUSTAFSSON[20]认为钢筋混凝土梁中混凝土所承担的剪切强度如式(3)：

vc/ft=k(d/lch)-0.25

(3)

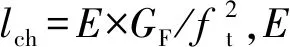
断裂过程区特征长度lch与断裂能有关，而断裂能GF又受梁有效高度影响，但式(3)并没有直接表征出vu和d的关系。另外，M.A.ISSA等[21]对6组不同高度的无腹筋钢筋混凝土梁断裂能试验研究表明：当梁高增加4倍左右时，平均断裂能只增加30%左右。结合式(3)可知：随着梁有效高度d的增加，钢筋混凝土梁的剪切强度将会减小。以上分析间接证明了无腹筋钢筋混凝土梁尺寸效应现象的存在，文献[20]的能量公式也为尺寸效应定量研究提供参考。

极限平衡法是取临界裂缝及顶端垂直截面所截的隔离体为研究对象建立的模型，结合混凝土本构关系建立平衡方程来分析无腹筋钢筋混凝土梁剪切强度。P.D.ZARARIS等[22-23]假定斜裂缝和水平方向夹角为45°，通过建立极限平衡方程得出了考虑尺寸效应的无腹筋钢筋混凝土细长梁剪切强度公式。文献[22-23]认为：在三点弯曲或四点弯曲作用下，无腹筋钢筋混凝土梁(细长梁)斜拉破坏是由剪跨区内混凝土劈裂破坏引起，同时与无腹筋梁剪切强度和临界剪压区高度有直接关系，故精确计算临界剪压区高度将有利于尺寸效应现象进一步研究。罗林等[24]在研究无腹筋钢筋混凝土梁剪切强度时对该问题有较为详细的解答，在分析影响临界剪压区高度的参数之后，通过试验数据曲线拟合得到各参数与临界剪压区高度的具体关系，这为研究无腹筋钢筋混凝土梁剪切强度尺寸效应现象提供了重要思路。基于此，文献[24]运用Z.P.BAŽANT提出的尺度律，得到了同时适用于斜拉破坏和剪压破坏的无腹筋钢筋混凝土梁剪切强度公式。但文献[24]提出的临界剪压区高度相关经验系数都是通过模拟Z.P.BAŽANT等[25-26]收集的无腹筋梁466个和12个数据得出的，参考数据相对较少，适用性较为有限。故进一步增大数据库，优化经验系数，有利于提出更精确的计算公式。

根据桁架模型，受力过程中各杆件均处于一维应力应变状态，形式简单、结构明确，便于分析和处理。自古典桁架模型被提出以来，众多学者对桁架模型进行了深化和拓展。E.MÖRSCH[16]对钢筋混凝土梁斜拉机理给出了清晰解释，并将桁架模型扩展到了受扭构件。但这些研究都忽略了斜裂缝上混凝土拉应力，其理论值较实际值偏小，过于保守。M.P.COLLINS等[27-28]在前人研究基础上，运用压力场理论、修正压力场理论将桁架模型进一步优化，并用来预测钢筋混凝土构件的剪切强度，提出了无腹筋、有腹筋钢筋混凝土梁剪切强度公式，并用于加拿大混凝土设计规范中。T.T.CHSU等[29]提出了软化桁架模型，该模型同修正压力场理论相似，假定了主应力方向和主应变方向一致，能较为精确地描述各类受剪结构性能。国内的学者运用桁架模型也对桁架理论进行了研究。魏巍巍等[30]在修正压力场理论基础上，对无腹筋钢筋混凝土构件受剪破坏做了进一步分析，提出了沿受弯构件斜裂缝表面平均剪应力的计算公式，并考虑混凝土构件尺寸效应提出了抗剪强度简化计算公式。但国内外学者的研究都是将不同尺寸的无腹筋钢筋混凝土梁统一化，建立适用于所有尺寸无腹筋钢筋混凝土梁抗剪模型，忽略了尺寸效应对无腹筋钢筋混凝土梁剪切强度的影响。

随着有限元技术在土木工程领域得到了广泛应用，学界运用有限元软件对钢筋混凝土剪切强度进行了研究。郑智辉[31]在ABAQUS中建立不同尺寸的无腹筋钢筋混凝土梁模型，采用黏结单元模拟混凝土开裂过程，结果表明：钢筋混凝土梁剪切强度存在尺寸效应现象，随着梁有效高度增加，尺寸效应现象越发明显；当梁尺寸继续增大，尺寸效应现象逐渐放缓，最后当梁尺寸达到某一数值时，尺寸效应现象趋于稳定。何龙军等[32]运用ADINA建立了无腹筋钢筋混凝土梁断裂力学模型，并进行了非线性分析：随着梁有效高度增加，各个阶段尺寸效应程度不一致；梁有效高度超过“起始尺寸”h1时，梁剪切强度尺寸效应越发明显；随着梁有效高度继续增加，当梁有效高度超过“终止尺寸”h2时，梁剪切强度尺寸效应现象已明显减弱。由于有限元软件分析钢筋混凝土梁抗剪强度步骤较多，每个步骤在操作过程中都会引入误差，这些误差累积往往会对计算结果造成灾难性影响，故其计算结果只能作为一个参考。

1.2 有腹筋钢筋混凝土梁尺寸效应的理论研究

美国混凝土规范ACI318-51[33]规定：当局部剪应力超过0.03f′c才会配置箍筋。美国俄亥俄州空军仓库发生梁剪切失效时，因仓库梁计算剪应力没有超过0.03f′c而没有配置箍筋，最后发生了剪切破坏。此后美国混凝土协会明确规定：所有梁中必须配置箍筋，并规定了最小配筋率，也开始对有腹筋钢筋混凝土梁剪切强度尺寸效应进行研究。

与无腹筋梁的抗剪机理不同，有腹筋钢筋混凝土梁在斜裂缝尚未形成时剪力时主要由混凝土传递，此时箍筋中的剪力一般很小；当斜裂缝出现后，混凝土传递剪力能力突然降低，这时与斜裂缝相交的箍筋剪力迅速增大；随着荷载继续增大，斜裂缝数量增加，裂缝宽度逐渐加大直至构件发生剪切破坏。由于箍筋限制作用，有腹筋钢筋混凝土梁剪切强度尺寸效应要弱于无腹筋梁。Z.P.BAŽANT等[34]对ACI-445F中有关钢筋混凝土梁剪切强度的数据库进行分析，证实了箍筋只能减弱钢筋混凝土梁的尺寸效应而不能消除尺寸效应。在式(1)基础上，Z.P.BAŽANT等[17]对经验常数λ0进行了修正，得到适用于有腹筋钢筋混凝土梁的经验常数λ′0，如式(4)：

(4)

式中：ρv为箍筋的配筋率；ρ0为经验常数。

由式(4)可知：λ′0>λ0，因此相对于无腹筋梁，有腹筋梁尺寸效应要弱一些。不考虑尺寸效应有腹筋梁剪切强度公式为：vu=vs+vc(vs为箍筋提供的剪切强度)。对有腹筋钢筋混凝土梁，尺寸效应仅对混凝土提供的剪切强度vc造成影响，而不是对整个有腹筋梁剪切强度vu造成影响，故考虑尺寸效应有腹筋梁剪切强度如式(5)[17]：

(5)

还有学者对有腹筋梁抗剪强度进行了研究，包括魏巍巍等[35]、常生福[36]，他们分别所得出的抗剪强度计算式与试验数据吻合都较好，但由于所选择的试验数据容量较小，代表性有限，也没有考虑梁剪切过程中存在的尺寸效应现象，故计算式无法进行推广。

相对无腹筋钢筋混凝土梁，有腹筋钢筋混凝土梁抗剪机理更为复杂，影响其抗剪强度因素更多。除影响无腹筋钢筋混凝土梁剪切强度的所有因素外，还包括箍筋强度、间距、绑扎形式、弯起钢筋角度、弯起钢筋弯起位置等等。虽然两者抗剪机理复杂程度不一样，但两者的剪切强度公式可进行简单的统一，传统方法是将混凝土抗剪贡献vc和箍筋抗剪贡献vs简单叠加，实际上vc、vs相互影响。若考虑配置箍筋对混凝土剪切强度提高，可引进系数α，则钢筋混凝土梁剪切强度有：vu=(1+α)vc+vs[37]。

当然要对有腹筋钢筋混凝土梁剪切强度尺寸效应现象进一步研究，还得抓住临界剪压区高度这一关键因素[38]。临界剪压区是钢筋混凝土梁受剪过程的核心部位，随着临界剪压区高度变化，在剪压区内的受力途径也会发生相应变化，临界剪压区高度直接影响因素有：混凝土强度、配箍率、纵筋率、剪跨比等。故建立临界剪压区高度的计算公式成为研究钢筋混凝土梁剪切强度的关键。

2 试验研究

基于理论研究，学界借助大量试验数据进行了数理统计方面分析，如：Z.P.BAŽANT等[17, 25]、罗林等[24]、G.RUSSO等[39]。学者们研究了影响钢筋混凝土梁剪切强度的主要因素，并得到了具有一定可靠度的经验公式。基于不同目的和准入准则，国内外学者和机构整理了相关试验数据库，如：文献[25]、文献[40]、文献[41]，文献[42-43]，文献[44]等，但目前尚未有专门针对基于尺寸效应钢筋混凝土梁剪切强度的试验数据库。

2.1 基于尺寸效应的无腹筋钢筋混凝土梁剪切强度的试验研究

若要得到基于尺寸效应的无腹筋钢筋混凝土梁剪切强度，完善无腹筋钢筋混凝土梁抗剪机理、建立梁剪切强度试验数据库亟待解决。众多学者对不同梁高的钢筋混凝土梁做了大量抗剪试验研究。

文献[45]对106根无腹筋钢筋混凝土梁进行试验分析，证实了名义剪切强度不但取决于材料性质，还和纵向钢筋数量、刚度和梁高度等因素有关；同时也意识到钢筋混凝土梁存在尺寸效应现象，但没有用数学术语来描述这些因素的具体关系，故其重要发现没有引起学界的重视。

G.N.J.KANI[46]对4组共31根不同高度的无腹筋钢筋混凝土梁进行抗剪试验发现，当梁有效高度从200 mm增加到800 mm时，剪切强度vu平均降低50%左右。常生福[36]认为：随着梁有效高度增加，传统钢筋混凝土梁剪切强度理论值与实际值相差较大，构件偏于不安全。

P.S.CHANA[46]通过5组共36根无腹筋钢筋混凝土简支梁试验[纵筋配筋率为1.8%，剪跨比a/d=3，包含截面尺寸(200×400)mm的原型试件和缩尺比例分别为1∶2、1∶3.3、1∶8.5的模型试件]得到无腹筋钢筋混凝土梁剪切强度存在较明显尺寸效应现象的结论。

T.SHIOYA等[48]通过均布荷载下无腹筋梁试验发现：梁有效高度从200 mm到3 000 mm时，梁的平均剪切强度降低达64%；无腹筋钢筋混凝土梁无论受集中荷载还是均布荷载都存在尺寸效应现象。

Z.P.BAŽANT等[26]对2组二维几何相似(二维相似即梁长、梁有效高度成比例，梁厚度保持不变)的无腹筋梁进行抗剪强度缩尺试验，其中一组纵筋呈直线状态，另一组纵筋末端垂直弯起(起到锚固作用)。试验表明：随着裂缝传播，梁储存能量开始释放，梁破坏时表现出很强的尺寸效应；锚固后梁脆性系数β(β=d/d0)大，锚固梁的剪切强度大于无锚固梁的剪切强度；但开裂强度几乎没有表现出尺寸效应。

J.WALRAVEN[49]对10根无腹筋钢筋混凝土梁进行了抗剪试验。其中：素混凝土梁3根，纵向配筋率为0.15%的试验梁3根，纵向配筋率为0.3%的试验梁4根。试验结果显示：无论是素混凝土梁还是钢筋混凝土梁都表现出很明显的尺寸效应现象；对于短梁(a/d≤2.5，a为梁的净跨，d为梁的有效高度)和细长梁(a/d>2.5)尽管破坏类型不同，但都表现出尺寸效应现象这一共性。

H.TAN等[50]对3组(剪跨比a/d分别为0.56、0.84、1.13，每组4根，有效高度d分别为150、250、440、1 560 mm)无腹筋钢筋混凝土深梁进行抗剪试验，其中2组梁都表现出很明显的尺寸效应。试验结果显示：钢筋混凝土梁开裂强度与尺寸大小无关，但其剪切强度存在尺寸效应；剪跨比越大，则钢筋混凝土梁尺寸效应越明显；当梁有效高度超过884 mm时，梁剪切强度尺寸效应现象有所减弱。

ZHANG Ning等[51]对3组(每组4根，梁有效高度分别为80、250、310、900 mm)无腹筋钢筋混凝土深梁进行剪切试验，其试验结果并没有表现出很明显的尺寸效应现象。文献[51]认为：产生该现象原因是施加荷载的承压板宽度会改变钢筋混凝土梁传力路径。总结文献[50-51]的试验，某些试验数据没有看出钢筋混凝土梁的尺寸效应现象，这并没有否定尺寸效应现象的存在，这和试验条件有关。文献[50-51]都是对钢筋混凝土梁深入研究发现，斜压破坏可能性最大。在斜压破坏这种小剪跨情况下，荷载垫板下垂直压应力σy不可忽略。这时混凝土处于双压加剪情况，这种情况的强度试验资料很缺乏。根据施岚青[52]的研究，σy的存在使剪切强度有较大提高。故小剪跨时，随着剪跨比减小，虽然破坏截面上正应力σx减小，但垂直压应力σy不断增大，所以剪切强度随着剪跨比减小而不断提高。这也说明了在进行钢筋混凝土梁抗剪试验研究时，应注意试验条件对钢筋混凝土梁剪切强度影响。

E.G.SHERWOOD[53]进行了无腹筋钢筋混凝土梁抗剪试验(试验分为2组，梁有效高度分别为280、1 400 mm)，较系统地研究了截面高度、纵筋配筋率、最大骨料粒径等因素对无腹筋梁剪切强度的影响。试验结果显示：梁有效高度为1 400 mm时的平均剪切强度为0.64 MPa；梁有效高度为280 mm时的平均剪切强度为1.12 MPa，大尺寸梁平均剪切强度为小尺寸的57%。

K.H.YANG[54]对4组(每组混凝土抗压强度不同，每组4根，梁有效高度分别为400、600、750、1 000 mm)无腹筋钢筋混凝土深梁进行抗剪试验得出：无腹筋钢筋混凝土梁剪切强度与梁有效高度d的比例关系，即普通无腹筋钢筋混凝土梁剪切强度vu∝d-0.26，含砂轻质粒料混凝土梁剪切强度vu∝d-0.65，轻质混凝土剪切强度vu∝d-0.71。由此可见，尺寸效应与混凝土类别有关。较普通混凝土梁，轻质混凝土梁尺寸效应更为明显。L.H.SNEED等[55]为了研究截面高度对受剪承载力影响，对6根无腹筋梁进行了抗剪试验，试验梁的截面为矩形，梁有效高度为305～915 mm，也证实了无腹筋钢筋混凝土梁存在尺寸效应现象。

于磊等[56-57]对9根大尺寸无腹筋钢筋混凝土梁进行了剪切试验。试验表明：试件开裂强度和剪切强度都呈现出明显尺寸效应现象；无腹筋梁有效高度为1 000 mm时比500 mm时开裂强度减小31%，剪切强度减小26%；截面有效高度为1 200 mm时比500 mm时开裂强度减小34%，剪切强度减小41%。

D.B.BIRRCHER等[58]对3组(每组4根，梁有效高度分别为：500、980、1 750 mm)无腹筋钢筋混凝土深梁进行了抗剪试验，其中2组表现出很明显的尺寸效应现象，另一组剪跨比a/d>2.5的试验梁没有明显的尺寸效应现象。

2.2 基于尺寸效应的有腹筋钢筋混凝土梁剪切强度的试验研究

相对于无腹筋梁，对腹筋钢筋混凝土梁的试验研究相对较少。笔者认为有以下两方面原因：① 有腹筋梁剪切强度尺寸效应弱于无腹筋梁；② 有腹筋梁剪切强度尺寸效应机理比较复杂。

M.P.COLLINS等[40]进行了一系列无腹筋(梁高为1 000 mm)和配有少量箍筋的钢筋混凝土简支梁在集中荷载作用下的剪切试验。试验结果表明：钢筋混凝土梁剪切强度尺寸效应不仅存在于无腹筋钢筋混凝土梁中，配有少量箍筋的大尺寸钢筋混凝土梁剪切强度尺寸效应仍然十分明显，也指出美国、中国等国家的混凝土规范存在有不安全因素。

刘立新等[59]对11根有腹筋钢筋混凝土梁进行了抗剪试验。其中：6根梁为集中荷载加载，5根为均布荷载加载，试验梁竖向腹筋率为ρsv=0.13%～0.21%，水平腹筋率为ρsh=0.2%～0.29%。试验表明：无论集中荷载还是均布荷载，同等条件下有效高度为500 mm的梁先于有效高度为400 mm的梁被破坏，剪切强度随着有效高度增加而减小。

E.J.TOMPOS等[60]对6根钢筋混凝土梁进行了抗剪试验。其中：5根为有腹筋，1根为无腹筋。5根有腹筋梁中2根梁有效高度为850 mm，其余3根有效高度为425 mm。试验结果表明：在同等条件下，大尺寸梁的破坏早于小尺寸梁，尺寸效应现象明显；箍筋能显著提高混凝土梁剪切强度，提高程度与箍筋强度、间距和绑扎形式有关，闭合箍筋比U形箍筋对混凝土梁剪切强度提高更为有效。

杜修力等[61]在低周反复荷载作用下对5 组不同尺寸钢筋混凝土梁进行抗剪试验。得到如下结论：在低周反复荷载作用下，钢筋混凝土梁剪切强度存在非常明显的尺寸效应现象，钢筋混凝土梁的强度、延性等力学性能均随截面尺寸增大而降低，钢筋混凝土梁承载力安全储备呈减小趋势。

于磊[57]在7根无腹筋钢筋混凝土梁基础上增加了4根试验梁(包括2根有腹筋梁，9根无腹筋梁)，在有效高度为500～1 200 mm的大尺寸钢筋混凝土梁上进行了抗剪试验。结果表明：与相同尺寸的无腹筋梁相比，箍筋可显著提高试件剪切强度；有腹筋梁尺寸效应要弱于无腹筋梁。

学者们对钢筋混凝土梁抗剪试验证实：无论是何种加载(集中，包括三点弯曲、四点弯曲或分布荷载，如图3)和支撑(简支或悬臂)条件下，缩尺和足尺无腹筋或有腹筋钢筋混凝土梁在剪切过程中均存在尺寸效应现象。对于有腹筋钢筋混凝土梁，从加载到破坏，箍筋制约了裂缝产生和发展，因而有腹筋钢筋混凝土梁尺寸效应现象要弱于无腹筋钢筋混凝土梁。目前，有腹筋钢筋混凝土梁尺寸效应的具体定量关系尚不明确，需进一步研究。

图3 荷载加载示意Fig. 3 Distributed loads diagrams

3 结论与展望

随着我国基础设施、城市/城际公共交通、水利工程等多项重大工程项目的推进，其结构件向着大跨度、大尺寸方向发展。随着工程界对结构件可靠度要求越来越高，基于尺寸效应的钢筋混凝土梁剪切强度研究会沿着以下几个方面发展：

1)随着试验研究条件和认识水平提高，将会大批量进行有腹筋钢筋混凝土梁抗剪试验，进行大尺寸、高承载能力的钢筋混凝土梁抗剪试验，完善钢筋混凝土梁剪切强度试验数据库；

2)针对钢筋混凝土梁尺寸效应研究相对较少，随着钢筋混凝土梁抗剪机理认识深入、大尺寸钢筋混凝土梁试验累积，将大力研究钢筋混凝土梁剪切强度尺度律；

3)在考虑大尺寸有腹筋钢筋混凝土梁抗剪机理基础上，加深对梁剪切强度机理认识，将尺寸效应引入基于小尺寸构件研究结果现行的钢筋混凝土梁设计理论，建立基于尺寸效应的钢筋混凝土梁的剪切强度公式。