改进的主成分分析法在皮棉质量评价中的应用

舒服华

武汉理工大学 继续教育学院（中国）

优良的原材料是获得高品质纺织品的基础。皮棉是一种传统的纺织品原料，在所有纺织品原料中其使用量占比过半。不同品种棉花产出的皮棉质量不尽相同。不同产地的同一品种，由于生长环境和管理水平不同，皮棉质量也有差异［1－2］。掌握皮棉质量鉴别技术，是采购优质原料的前提。中国已针对皮棉的质量检验评价制定了相关等级标准，但等级数量有限。仅按照标准等级衡量皮棉质量远远不够，需进一步细化皮棉的质量指标，并采用综合评价法判定指标的合理性。目前的综合评价方法很多，各自存在优点与不足。其中，主成分分析法是将相互之间具有关联性的数量较多的指标转化为少数几个线性无关的综合指标。这些综合指标称为主成分，代表原始指标的大部分信息，且各个主成分所含信息互不重复。这样，可将复杂因素归纳为几个主要成分，降低数据处理的复杂性，使研究问题简化，同时，研究结果又不失真实性。主成分分析方法在很多领域得到了广泛应用［3－8］。本文尝试采用改进的主成分分析法评价皮棉质量，以降低评价难度，提高评价效率。

1 主成分分析法简介

1.1 主成分分析基本原理

在现实生活中，往往会遇到许多变量，这些变量的内涵或数据存在交叉重叠，给研究带来不便。主成分分析法可较好地解决这一问题。主成分分析法的基本原理是，通过降维方法处理，将多个数据间具有一定相关性的指标组合成一组新的不相关的指标。新指标为原指标的线性组合，包含了原指标中的绝大部分信息，可用来代替原指标，从而化繁为简，使多个相关指标转化为少数几个无关指标。

主成分分析法中主成分的信息量，主要取决于评价矩阵的相关系数矩阵的特征值大小，特征值越大，主成分信息量越多。特征值最大的主成分称为第一主成分，其次为第二主成分，以此类推。特征值个数等于原指标的个数，对应的主成分也就与原指标数目相同。选取主成分时，没有必要选取所有主成分，否则，新指标的数量就与原指标一样多，主成分分析也就失去了意义。事实上，越往后的主成分信息量越少，有些甚至无限接近0。因此，一般只需选取累积贡献率在85%～90%的少数几个主成分即可。

假设有n个评价对象，m个评价指标，构成评价矩阵X ＝ （xij）n×m，即

其中，xij为第i个评价对象第j个评价指标的评价值（j＝1，2，…，n）。

这m个线性相关的评价指标可以通过正交变换，重新组合成m个线性无关的新指标，即

其中，Fj为第j个主成分，aij为第j个主成分的第i个指标的载荷系数。

主成分分析模型可表示为

A称为主成分系数矩阵。

大部分新指标所包含的信息量减少，在选取主成分时可以舍去。

1.2 主成分分析评价法步骤

1.2.1 数据标准化

数据标准化分为两个步骤，第一步是消除指标量纲及方向性影响。消除方向性影响意即将所有类型的指标都转化为效益型指标（值越大越好），主要是针对成本型指标（值越小越好），需将其转化为效益型指标。

当xij为效益型数据时，数据规范化方法为

当xij为成本型数据时，数据规范化方法为

式中，xij为第i个样本第j个指标的原始数据，yij为第i个样本第j个指标的规范化数据。

第二步为调整数据的分布，使每个指标数据的均值为0、标准差为1，即

式中，rij为标准化数据，μj为第j个指标的均值，σj为第j个指标的标准差。

1.2.2 构建相关系数矩阵

相关系数矩阵由指标之间的相关系数构成，其每1行每1列代表1个相应的指标。计算各个指标的相关系数，按照指标的排列顺序，以及各指标间的相关系数构造相关系数矩阵。相关系数矩阵为一对称矩阵。

1.2.3 计算特征值和特征向量

计算相关系数矩阵的特征值和对应的特征向量，将特征值从大到小排序。特征值即相应主成分的系数，其大小反映了主成分的影响力。

1.2.4 计算贡献率和累积贡献率

式中，ci为主成分Fi的贡献率，pi为F1到Fi的累积贡献率，λi为Fi的特征值。

1.2.5 提取主成分

提取累积贡献率大于90%的特征值λ1、λ2、…、λt，对应的主成分为F1、F2、…、Ft。

1.2.6 计算主成分综合得分

1.2.7 得出评价结果

根据评价对象的综合得分判断优劣，综合得分越高，评价对象越优。

1.3 主成分分析改进

传统的主成分分析法忽视了各评价指标对评价对象的影响程度，将各评价指标对评价结果的重要性均等看待，影响了评价结果的客观性。为了体现不同的评价指标对评价结果的影响程度不同，本文采用对指标赋予权重的方法加以改进，以提高评价结果的真实性。因皮棉评价指标较多，故指标的权重采用较为简单的环比评分法确定。环比评分法容易操作，评分的可塑性、可控性较大，能够较准确地表达不同指标对评价结果的影响。具体方法：根据各评价指标对评价结果的影响大小，对其重要性进行评分，评分可以为百分制、十分制，也可以为小数、分数。计算各个评价指标得分的比重，即各自的权重。设评价指标Xi的重要性评分为Bi，则Xi的权重为

2 基于主成分的皮棉质量评价

以8个不同供应商销售的锯齿棉为研究对象，其评价指标集为s＝（s1，s2，…，s8）。参照国家标准，皮棉质量及等级划分的主要指标如下：成熟系数（X1）、断裂比强度（X2）、黄根率（X3）、毛头率（X4）、纤维长度（X5）、马克隆值（X6）、异纤维含量（X7）、回潮率（X8）、含杂率（X9）、短纤维率（X10），本文选取以上10项指标作为皮棉质量评价的指标。评价指标集为X＝（X1，X2，…，X10），按照相关标准测试这8种试样的10项指标，结果如表1所示。

表1 锯齿棉指标测试结果

2.1 数据规范化

首先，消除指标的量纲和方向性。10项评价指标中，成熟系数（X1）、断裂比强度（X2）、纤维长度（X5）、马克隆值（X6）值越大越好，为效益型指标，按照式（3）规范化处理。黄根率（X3）、毛头率（X4）、异纤维含量（X7）、含杂率（X9）、短纤维率（X10）值越小越好，为成本型指标，按式（4）规范化处理。由表1可以看出，8种试样的回潮率均在8.0～10.5范围内，而该范围的回潮率越小越好，故对于本研究体系，回潮率（X8）也为成本型指标，同样按式（4）规范化处理。10项指标规范化处理结果如表2所示。

2.2 确定指标的权重

根据有关标准和实际经验，取这10项指标的重要性评分分别为B1＝10.00，B2＝9.75，B3＝9.50，B4＝9.25，B5＝9.00，B6＝8.75，B7＝8.50，B8＝8.25，B9＝8.00，B10＝7.75。根据式（9）计算得10项评价 指 标 的 权 重 分 别 为 w1＝ 0.112 7，w2＝0.109 8，w3＝0.107 0，w4＝0.104 2，w5＝0.101 4，w6＝0.098 6，w7＝0.095 8，w8＝0.093 0，w9＝0.090 1，w10＝0.087 3。

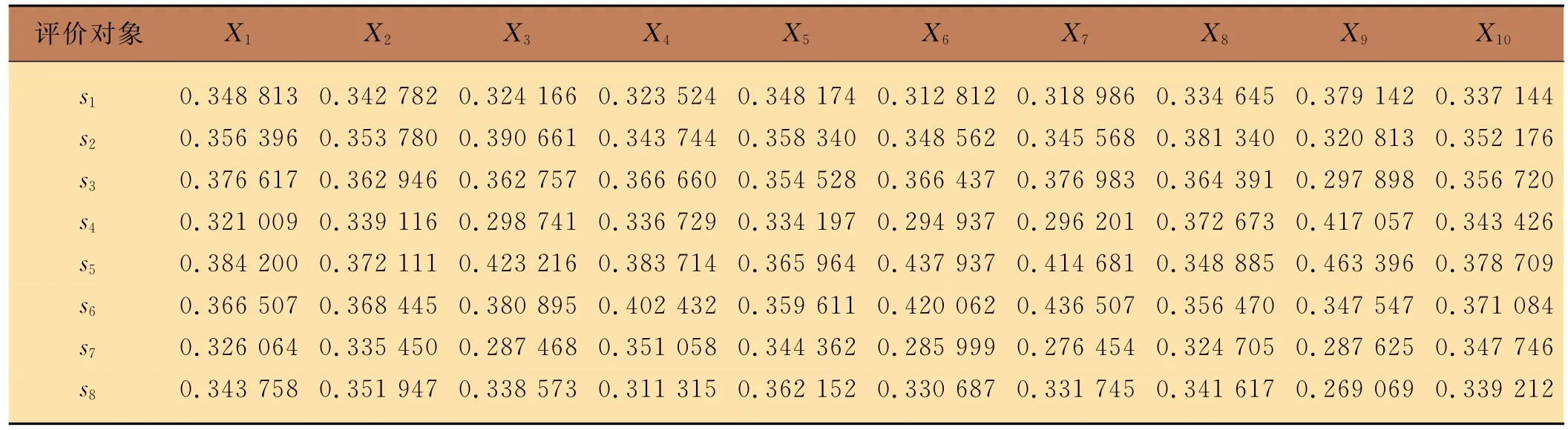
表2 规范化数据1

2.3 数据加权规范化

加权规范化数据结果如表3所示。

以加权规范化数据为基础，按式（5）将其转换为均值为0、标准差为1的分布，结果如表4所示。

2.4 构建相关系数矩阵

计算指标的相关系数矩阵，结果如表5所示。由表5可知，许多指标的相关系数大于0.5。其中，X1和X2的相关系数最大，为0.929 909。即这些指标存在很强的相关性，适合于运用主成分分析法。

表3 加权规范化数据

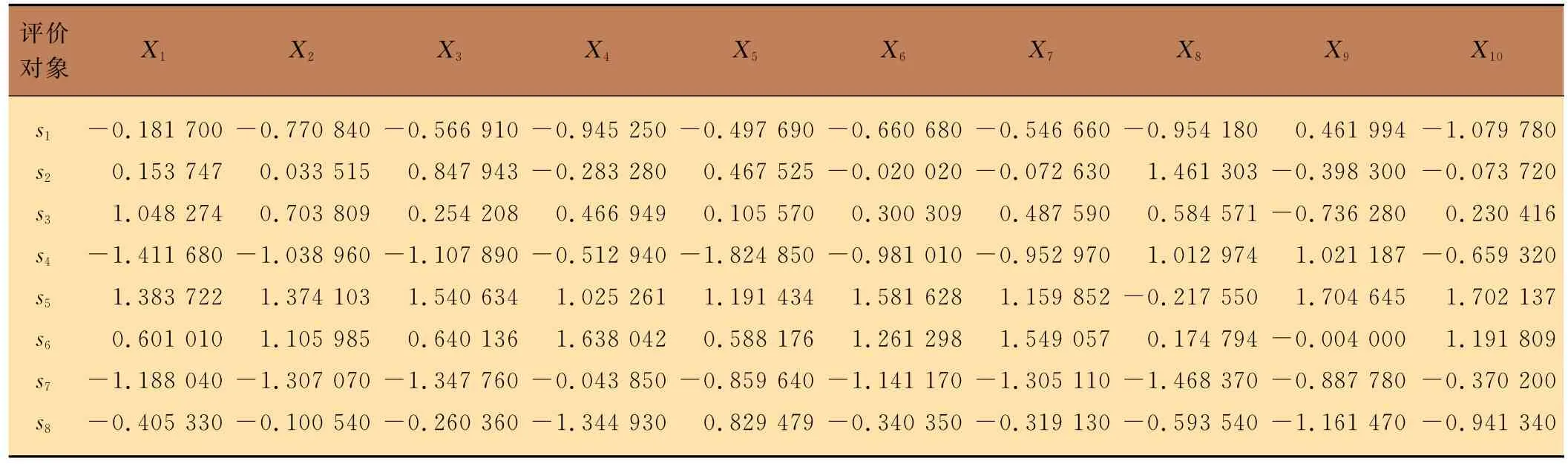
表4 规范化数据2

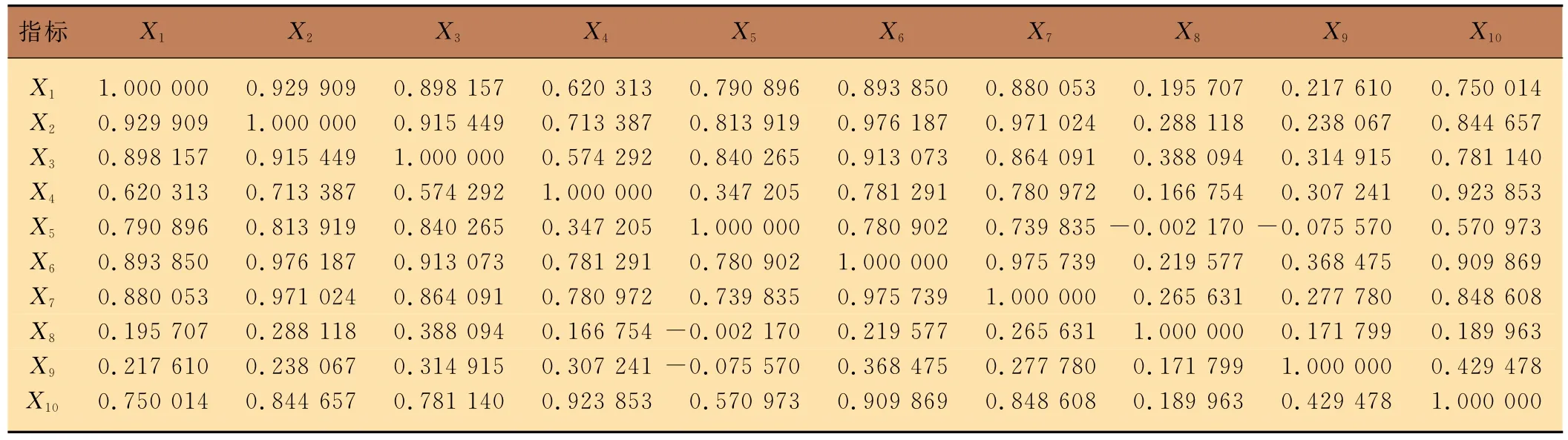
表5 相关系数矩阵（表格形式）

2.5 计算相关系数矩阵的特征值与主成分的贡献率、累积贡献率

首先计算相关系数矩阵的特征值，然后按式（6）和式（7）计算主成分的贡献率、累积贡献率，结果如表6所示。数据表明，主成分数与指标数相等，前几个的贡献率较大，越往后，贡献率越小。

表6 主成分特征值及贡献率

2.6 提取主成分

按照“选择的新指标个数累积能代表原指标信息的90%以上为止”原则，根据表6数据，提取主成分1、2和3，分别记为F1、F2和F3，它们的载荷系数如表7所示。

提取的主成分可表示如下。

F1＝0.352 021X1＋0.374 285X2＋0.358 097X3＋0.299 699 X4＋ 0.297 613 X5＋ 0.378 794 X6＋0.369 337 X7＋ 0.108 192 X8＋ 0.129 269 X9＋0.347 929 X10

F2＝－0.154 050X1－0.090 380X2－0.052 480X3＋0.231 345 X4－ 0.495 850 X5－ 0.001 530 X6－0.024 400X7＋ 0.412 114X8＋ 0.680 958X9＋0.178 383 X10

F3＝－0.047 190X1－0.071 530X2－0.219 420X3＋0.304 099 X4－ 0.075 160 X5＋ 0.071 378 X6＋0.004 301 X7－ 0.847 760 X8＋ 0.255 579 X9＋0.239263 X10

表7 主成分载荷系数

主成分F1、F2和F3为综合新变量，它们由原10项指标线性组合而成，且线性无关，互不重复，并包含了原指标90.76% 的信息，可替代原指标X1、X2、…、X10对评价对象进行评价。

2.7 计算评价对象的综合得分

评价对象的综合得分（F）为提取的主成分与对应贡献率积之和，即

F ＝0.686 568F1＋0.126 001F2＋0.095 040F3

由此计算得各评价对象的综合得分如表8所示。数据表明，s5综合质量最优，s7综合质量最差。评价结果直观图如图1所示。

表8 评价对象的综合得分

图1 评价结果直观图

3 结语

棉花的品质、生长环境、管理水平、收获方式及加工精度不同，导致皮棉质量存在很大差异。科学评价皮棉的质量，一方面对指导棉纺织企业采购优良的原料，生产高品质产品，满足消费者对美好生活的追求具有重要意义；另一方面可促进棉农引种优良品种，提高种植技术，促进皮棉质量的提高。衡量皮棉质量的指标较多，涉及面广，并且有些指标存在一定的关联，需采用有效方法，才能得到客观公正的结果。主成分分析法的实质是通过正交变换，将一组线性相关的变量转换为另一组线性不相关的变量，删除多余重复内容。在构建新变量时，选择性地采用几个主要新指标，保持绝大部分原有信息，达到在求解结果不失偏差的前提下，简化问题，提高求解效率的目的。本文运用改进的主成分分析法评价皮棉质量，较好地解决了评价指标相关性问题，可为纺织企业高效评价皮棉质量提供借鉴。