一种高精度加权最小二乘算法

王向阳， 蔡成林， 张文波， 蔡 劲

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

北斗卫星导航系统是我国自行研制的全球卫星导航定位系统，广泛应用于交通运输、海洋渔业、水文监测等领域[1]。随着北斗卫星导航系统建设的快速发展，国内外学者对接收机钟差、电离层、对流层等相关误差进行了研究，分析并纠正了相关误差后，评估了伪距单点定位的精度。传统的伪距单点定位算法有最小二乘(least square，简称LS)算法[2]、高斯牛顿迭代最小二乘(Gauss-Neton iterative least square，简称GNILS)算法[3]、Kalman滤波算法等。由于GNILS算法的定位精度较LS算法高，目前伪距单点定位普遍采用GNILS算法。利用GNILS算法进行定位解算时，对观测站坐标的初始值的依赖性较大，若选取观测站坐标的初始值与真实值存在较大偏差，迭代次数将会增加，计算量也随之增加[4]。鉴于此，提出了一种不等权的自适应加权最小二乘(adaptive weighted least squares，简称AWLS)算法。通过北斗实测数据验证表明，AWLS算法计算复杂度低，定位精度高，并能有效地排除误差较大卫星对定位平稳性的破坏，有利于接收机实现高精度的定位和导航，可提高伪距单点定位的精度。

1 GNSS伪距单点定位原理

在伪距单点定位的过程中，电离层延迟误差、对流层延迟误差、接收机钟差等因子会对定位结果造成较大影响[5-7]，因此将伪距的观测方程设为：

(1)

其中：

针对以上参数误差，卫星钟差dti可通过星历参数进行修正；电离层延迟误差dion,j可通过模型进行修正；对流层延迟误差dtrop,j可通过Saastamoinen模型进行修正[9-11]。误差修正后的伪距方程为：

(2)

式(1)减式(2)可得Δρi=-(dρi+ερ)。

2 GNILS算法

GNILS算法作为传统的北斗伪距单点定位算法，在进行定位解算时，根据已知的初始估计值来求解多元非线性方程组，将各个非线性方程在初始估计值处线性化，再根据LS算法原理求解线性化方程，得到解的更新值，并重复这种运算逐次迭代，直至所得结果达到所要求的精度，进而求解接收机的位置坐标[12]。

式(2)的原型为ki=ri0+cdt-ρi，由于Δρi=-(dρi+ερ)非常小，可假设其为零，则式(2)可简化为：

ki=Ixi·Δxj+Iyi·Δyj+Izi·Δzj-cdt。

(3)

其中：

根据最小二乘原理，得

Δx=(GΤG)-1GΤB。

(4)

其中：

(5)

求出4个估计量(Δxj,Δyj,Δzj,cdt)，更新X0=(x0,y0,z0,B0)，令x0=x0+Δx，y0=y0+Δy，z0=z0+Δz，B0=B0+cdt，重复上述过程进行迭代，直到Δxj,Δyj,Δzj满足：

(6)

设定一个阈限值α，其取值8～15，迭代次数不超过10次，当式(6)成立时，解算出来的值即为GNILS算法求解出的用户接收机坐标和接收机钟差[13]。

3 AWLS算法

AWLS算法与GNILS算法相同的是都需要进行算法迭代，不同之处在于是否构建加权系数矩阵。用AWLS算法构建加权系数矩阵的方法如下：

对于式(2)的原型，

ki=ri0+cdt-ρi

的前2项

ri0+cdt=

其为线性化后的伪距值，后一项ρi为修正后的伪距，虽然后者在实际情况中修正并不完全，还存在一些误差，但这些误差相对ρi本身来说是一个非常小的量，即ρi为第i颗卫星与用户实际位置相对应的含有较小误差的伪距，ki为第i颗卫星与接收机实际位置相对应的含有较小误差的伪距与线性化后的伪距之间的偏差。设k为所有可用卫星与用户实际位置相对应的含有较小误差的伪距值与线性化后的伪距值之间的偏差，令

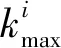
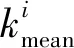
(7)

定位结果最佳。

AWLS算法构造的权系数矩阵Γ是以卫星与接收机实际位置相对应的含有较小误差的伪距与线性化后的伪距之间的偏差ki为基础的，它是一个自加权矩阵，随着迭代的进行，会随接收机位置的更新而改变。利用此原理，该矩阵能够极大地降低问题卫星对定位结果的影响，使定位结果更佳。

根据加权最小二乘算法原理：

Δx2=(GΤΓG)-1GΤΓB，

(8)

求出4个估计量(Δxj,Δyj,Δzj,cdt)，更新X0=(x0,y0,z0,B0)，令x0=x0+Δx，y0=y0+Δy，z0=z0+Δz，B0=B0+cdt，重复上述过程进行迭代，直到Δxj,Δyj,Δzj满足：

(9)

设定一个阈限值β，其取值范围8～15，迭代次数不超过5次，当满足式(9)时，解算出来的值即为AWLS算法求解出的用户接收机坐标和接收机钟差。

4 算例评估

通过对北斗数据进行分析与仿真来验证AWLS算法的优越性，其中北斗数据从安装于桂林电子科技大学的清华高精度接收机中获取，采用的是2018年3月14日到2018年3月18日的BDS数据，该数据是以30 s为一历元并连续接收24 h。

在进行定位解算时，考虑到较好的卫星高度角可在一定程度上降低多路径效应等因素对定位精度的影响，设置卫星的截止高度角为15°。通过多次实验验证，卫星的截止高度角为15°时，接收机可接收到足够多的可用卫星数，且定位精度最优。对BDS数据进行处理分析，通过星历参数和相应的简单算法求解卫星的位置，通过Klobuchar模型对电离层延迟进行修正，Saastamoinen模型对对流层延迟进行修正等，进而得到修正后的伪距[14]，如表1所示。利用上述算法得到的卫星的位置坐标、修正后的伪距，通过LS算法、GNILS算法、AWLS算法求解用户接收机的水平定位精度、高程定位精度、三维定位精度[15]，所得结果如表2所示。

由表2可得以下结论：

1)AWLS算法和GNILS算法相比于LS算法，抗差性能和定位精度都有较大提高；

2)AWLS算法相比于GNILS算法迭代次数少，计算复杂度降低；

3)AWLS算法相比于GNILS算法,抗差性能和定位精度提高约2倍。

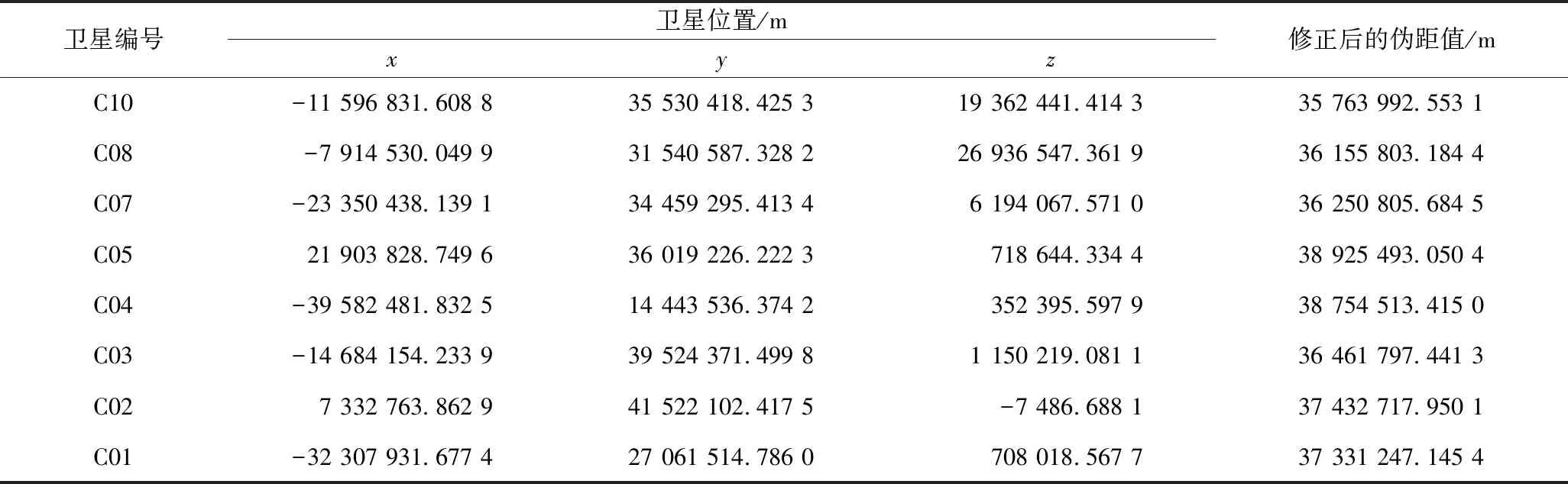
表1 某个历元的卫星位置坐标和修正后的伪距值

表2 三种算法的定位结果比较

图1 GNILS算法定位结果

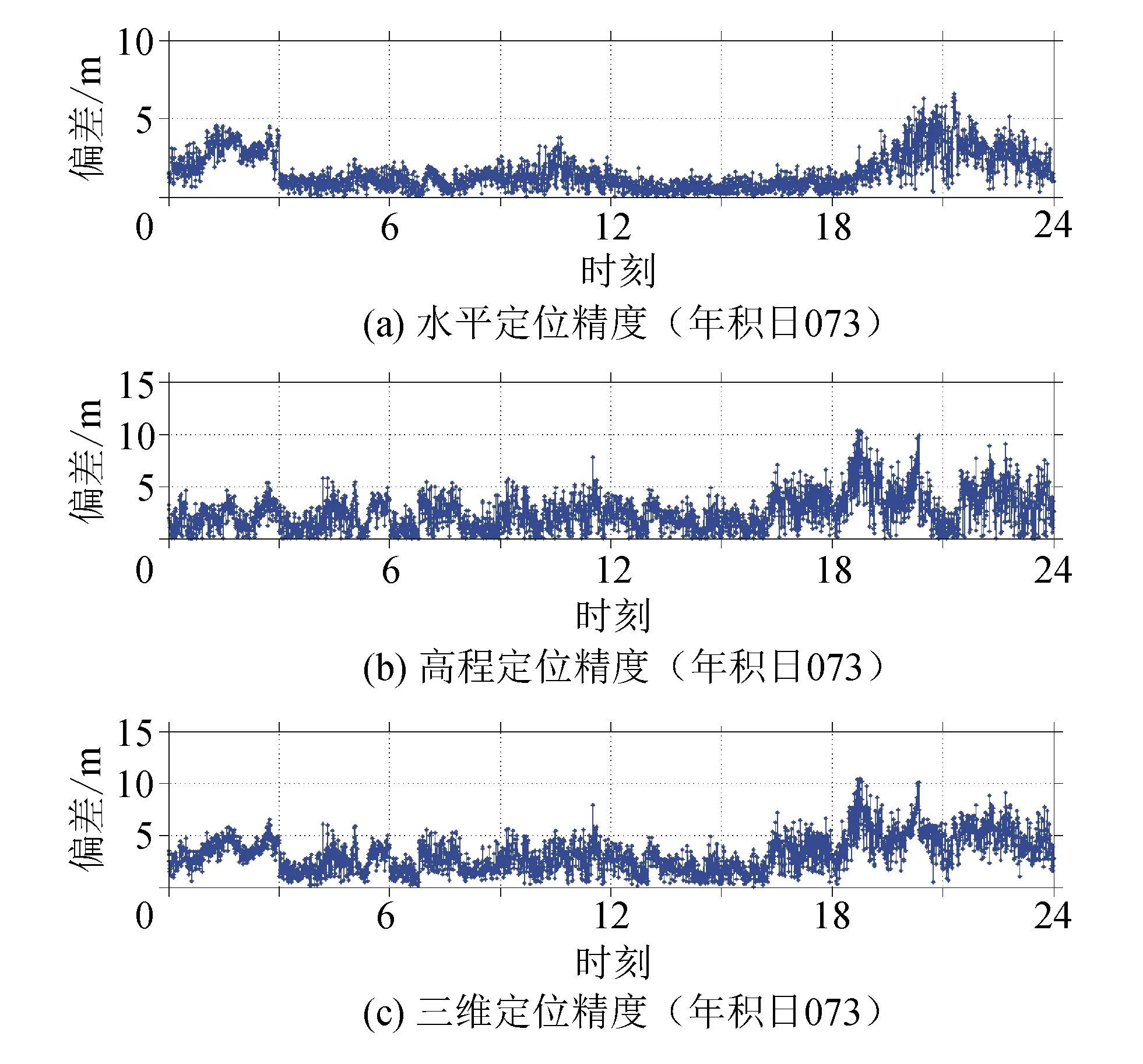
图2 AWLS算法定位结果

从图1、2可看出，AWLS算法的定位精度比GNILS算法高，且抗差性能更好,但在18-24这个时间段，幅度较大，精度稍差，但总体来说，AWLS算法相对于传统的LS算法和GNILS算法较优。

5 结束语

在分析最小二乘法(LS)和高斯牛顿迭代最小二乘算法(GNILS)的基础上，提出了一种改进的高精度的加权最小二乘(AWLS)算法，并在北斗PVT性能测试评估中进行仿真。该算法利用伪距偏差最大的卫星在定位解算中的权重尽可能小的原理构建一个自加权矩阵，解决了异常卫星对定位平稳性破坏的问题，并极大地提高了定位精度，使北斗伪距的单点定位精度提高到约3 m。