基于日涨跌率推动的股指序列建模和实证分析

周 霞， 涂 伟， 刘 聪， 程英杰

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

股票市场是投资者、经济学者和管理学者等共同关注的焦点，股票价格变化规律是投资者制定投资策略的理论依据。目前，基于神经网络或支持向量机的方法对历史价格序列进行建模拟合研究非常火热[1]。Guresena等[2]在2011年利用反向传播法(BP神经网络)对股指进行预测；Dong Guanqun等[3]运用BP神经网络对向前一步和多步的股价序列进行了预测和比较分析；Li Chunquan等[4]利用修正的简化粒子群算法结合推广的回归神经网络优化法对股票市场进行预测；Zhang Qiuming等[5]将灰色模型和神经网络应用于股票市场的预测中；Zhang Xiangzhou等[6]从特征选择的角度切入,运用CART决策树等算法找出影响股价波动趋势的关键因素；Sai Ying等[7]运用支持向量机方法对中国股市特征进行了回归预测。另一类研究方法是以统计原理为基础对股价波动规律进行预测，比较有代表性的模型包括ARCH模型和SV模型。Azevedo等[8]利用数据挖掘技术和时间序列分析对短期股票市场进行预测的方法进行总结；Tsai等[9]研究了不同时间尺度下股票价格序列的特征，并对历史K线图相互之间的相似性关系做出了分析；刘叶玲等[10]利用广义线性回归的方法进行建模，从而预测股票价格；程昌品等[11]采用小波分解对股价序列进行分析,将序列中的低频信息和高频信息分离，分别运用支持向量机模型和ARIMA模型进行拟合，得到了较好的拟合效果。值得注意的是，这些方法都是针对交易时间或日历时间的时间进程来推进的序列进行研究。Clark[12]研究表明，价格的推进进程不仅仅是单纯的日历时间刻度，而是基于信息流的驱使。吴冲锋[13]从时间、股价、成交量的三维空间出发，用GARCH对基于成交量的股价序列和原收盘价和平均成交价时间序列进行误差自回归分析，进一步证实了维度转换思想应用于股价预测可行、有效。

股指作为反映整个股票市场上各种股票市场价格的总体水平及其变动情况的指标被广泛关注，它的走势也直接影响了股票市场及相关金融产品市场投资者的投资决策。2016年中国证券登记结算有限公司统计报告中指出：我国股市中自然人投资者人数达1.58亿，其中投资金额在50万以下的中小个人投资者占95.17%。大部分的中小投资者不具有专业的投资理论知识，日涨跌率成为其作出决策的重要指标。对于机构投资者来说，日涨跌率也是其投资所要考虑的一个重要指标。因此日涨跌率是股指波动的一个很重要的信息流。

基于以上分析，将日涨跌信息融入到股指中，将日涨跌率作为影响股指波动的一个重要因素，运用维度转换思想，构造一个以日涨跌率为维度的新的时间序列，再基于这个时间序列建立日涨跌率和价格的变动关系，通过AR-GARCH模型拟合该股指序列，进行实证研究。通过对比股指时间序列变换前后模型的拟合效果，进一步验证了维度变换方法的可行性。

1 基于日涨跌率推动的维度变换思想

在实际的金融市场和现实的经济世界中，研究变量应当以其自身的经济时间来推进，而不是以固定日历时间来推进。Stock等[14]也认为经济周期是一个独立的经济时间单位，而不是一个日历时间单位。由于经济周期的时间长度可能不像固定的日历时间周期(如年、季度、月、半月、周、日等)长度那么一致，将按照固定日历时间记录的经济变量时间序列按照经济时间序列进行分析，很难得到较好的预测效果。为了避免这一问题，可以将日历时间等固定的时间维度转化为交易信息流维度，如将时间维度转化为日涨跌率维度。这样做，既将日涨跌率融入股指序列，同时也符合市场交易本身按照信息流推进的假说。

以往的时间序列分析只是从模型上或者参数上重新构造，序列本身均按日历时间或者交易时间推进。若将日涨跌率这一信息流作为新的维度来进行研究，基于日涨跌率构建一个新的时间序列，将每日股指映射到不同长度的时间单位上，再重新计算每个单位时间长度内新的股指值，重构出新的股指序列，可以解决以往方法的不足。

2 基于日涨跌率推动的股指序列构造

2.1 构建基于日涨跌率推动的时间序列

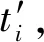
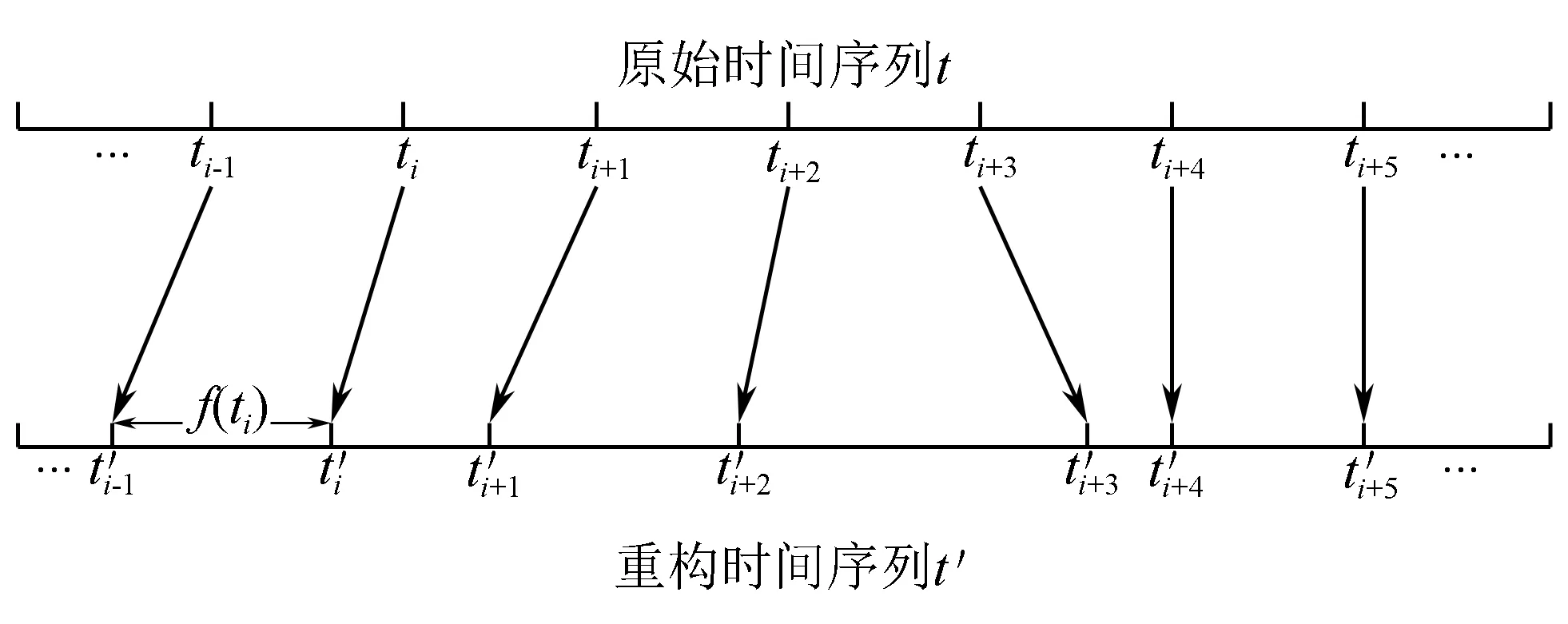
图1 基于日涨跌率的时间序列的构建图

2.2 构造基于日涨跌率的股指序列

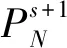
其中Pi为按照日历时间记录的第i天的原始股指。

2.3 建立模型

2.3.1 日涨跌率的度量方式

选取日波动率作为日涨跌率的度量因子：

Ft=|lnxt-lnxt-1|。

其中：Ft为第t日指数的波动率；lnxt为第t日指数的对数取值。

2.3.2 基于日涨跌率的时间序列和股指序列的映射关系

构造基于日涨跌率的时间序列，建立其与股指序列的映射关系。一般日涨跌率大的交易日，信息流含量高。这样，可以将Δf(ti)分为小范围的涨跌、中等程度涨跌和较大程度涨跌率。假设中等程度涨跌映射到时间轴上的经济时间长度不发生改变，为一个标准单位；小范围的涨跌的时间长度缩小为α个单位，其中α为大于0小于1的常数；较大程度的涨跌对应的时间长度为1+β，其中β表示一个正常数，根据时间长度总体量相等这一事实来确定。那么Δf(t)可表示为：

其中μ和σ分别为日波动率对数序列的均值和标准差。又因T-1∑Δf(t)=1，所以可求得

其中：

2.3.3 AR-GARCH模型

传统的OLS回归模型的重要假设包含误差项相互独立且具有同方差性。在对股指序列进行分析研究的过程中，时间序列残差往往存在相关性且具有明显的异方差特征。若依然沿用传统的OLS回归,会导致参数显著性和置信区间的统计检验不准确，同时还使得回归模型参数失效。基于此,采用AR-GARCH模型：

其中：xt为对数股指序列；εt为对数股指残差序列；νt为自回归残差序列；ht为条件方差序列；et为服从标准正态分布的随机变量序列；βk表示AR模型的参数;ηi表示ARCH参数;λj表示GARCH参数。

2.3.4 误差分析量

采用均方差、平均绝对误差、最大绝对误差、最小绝对误差、小于1.5%的绝对误差等来对所建立的模型进行检验和比较。设Rt、Pt分别为实际值和模型的预测值，样本数为N。

1)均方误差：

2)平均绝对误差：

3)最大绝对误差：

4)最小绝对误差：

5)小于1.5%的绝对误差：

其中：

3 实证研究

3.1 数据样本

选取上海证券交易所的上证综合指数(000001)，时间从1990-12-19-2009-08-25，共6554个交易日。选取上证综合指数(000001)作为实证研究的对象。

3.2 基本统计量

以日波动率作为日涨跌率的度量，日波动率和日波动率对数值的统计结果如表1所示。

3.3 基于日涨跌率的股指序列

根据日涨跌率时间序列和股指序列的映射关系公式，设α=0.5，可得β=0.402 8，其中小范围的涨跌、中等程度涨跌和较大程度涨跌的天数分别为2084、1883和2587。基于新构建的日涨跌率时间

表1 日波动率与日波动率对数值的基本统计量

序列，计算出新的经济时间序列下所对应的股指数。将上证指数序列、AR-GARCH模型拟合的股指序列与基于日涨跌率的股指序列的基本统计量进行比较，结果如表2所示。

表2 上证指数与基于日涨跌率的股指的基本统计量比较

3.4 建立AR-GARCH模型

将6553个样本分为2个部分:第1部分为1～5549个样本，约占总体的84.6%，用于模型识别和参数估计；第2部分为5550～6554个样本，约占总体的15.4%，用于模型测试。用逐步自回归方法确定误差自回归的阶数，进一步验证是否存在ARCH现象，根据AIC和SBC信息准则确定序列的阶数p和q。对改进前后的模型进行比较，结果如表3所示。

表3 模型的比较分析

通过对模型中的参数估计，得到原始日历时间下的股指序列和基于日涨跌率的经济时间序列下的股指模型分别为：

3.5 模型参数分析

对以上2个模型中的各参数进行分析，结果如表4所示。

表4 各序列模型的参数分析表

从表4可知：

1)2个序列的系数0.999 0和0.997 2均接近1，但小于1，说明该参数在统计学意义上是显著的。

2)从残差自回归系数AR(1)、AR(2)、AR(3)的T检验看，在第1个序列中存在部分参数不显著，即无法拒绝参数为零的假设，而第2个序列的T检验显示均显著不为零，这说明模型(5)较模型(4)更优。

3)2个序列的AR-GARCH模型的参数均显著不为零，说明模型1和模型2都很好地解决了原始指数序列中存在异方差的问题，即有效地刻画了原始指数序列的波动情况。

3.6 误差分析

将原始数据的AR-GARCH模型与基于日波动率的经济时间下的股指序列的AR-GARCH模型(以下称为“改进的AR-GARCH模型”)进行比较。在定阶阶段，辨识样本数据5549个，其样本数据基本统计量如表5所示；在测试阶段，样本数据1005个，其样本数据基本统计量如表6所示。

表5 AR-GARCH模型与改进的AR-GARCH模型定阶阶段的样本数据统计量表

表6 AR-GARCH模型与改进的AR-GARCH模型测试阶段的样本数据统计量表

通过比较表5、表6可知，无论在模型定阶部分，还是在测试部分，改进的AR-GARCH模型拟合指数序列的误差要小很多，效果较好，这说明该模型可以很好地拟合原始股指序列。另外，2种模型在辨识部分的误差相对于测试部分较大，这也说明通过模型定阶部分的数据所得出的模型表达式中的各参数是有效的，对于测试部分的样本数据的预测相对准确。

4 结束语

通过引入日涨跌率分析因子，构造基于日涨跌率推动的经济时间序列，基于该序列重构新的股指序列。实证研究表明，针对股指真实值的拟合，基于日涨跌率构造的股指序列比日历时间下的股指序列拟合更好，且误差值(均方差、平均绝对误差、最大绝对值误差、最小绝对值误差和绝对值误差小于1.5%的比例)明显缩小。实验结果表明该方法有效、可行。