基于模糊控制的MEMS陀螺仪数字驱动闭环设计

彭焮成， 王素娟， 刘玉县， 陈 婷， 汤 丽

(1.江西理工大学 机电工程学院，江西 赣州 341000； 2.广东顺德创新设计研究院，广东 佛山 528300)

0 引 言

微机电系统(MEMS)陀螺仪具有体积小、功耗低、成本低，抗过载能力强、动态范围大、可集成化等优点在工业控制、航空航天、汽车、消费电子、军事等领域中得到广泛应用[1]。陀螺是一种测量角速度的力学传感器，其工作前提是驱动模态能稳定振荡起来，需要合适的驱动环路。相对于采用模拟电路，数字电路闭环控制具有精确、对环境有效变化易于控制、容易对算法调整和优化的特点，并且由于现场可编程门阵列(field programmable gate array,FPGA)并行处理快速方式、硬件描述语言、模块化设计等优点，许多陀螺的数字电路设计方法搭建在FPGA平台上[2,3]。

本文使用了CORDIC算法[3]产生驱动信号和解调信号，相比于直接频率合成[4](direct frequency synthesis,DDS)方法节省了大量的只读存储器(read only memory,ROM)资源。因为直接频率合成是将信号正余弦波的幅值存入查找表中(look up table,LUT)，要达到高的精度将占用大量内存资源[5]。信号解调采用了工业上广泛应用的正交解调，相比于最小均方(least mean square,LMS)自适应滤波[6]要简单，并且不需要考虑滤波的权重系数。再经过低通滤波滤除由于解调产生的高频信号。参考幅值和相位可以由扫频方法[8]和振动测试方法[9]求得。陀螺的驱动模态是非线性系统，采用模糊控制具有优越的非线性控制能力使陀螺能够在谐振频率处稳定工作,得到最大的信噪比。

1 陀螺原理

如图1所示,MEMS陀螺驱动模态的运动学方程可以等效成二阶质量—弹簧—阻尼系统。

图1 MEMS陀螺仪简化模型[7]

设驱动模态的弹簧系数kd,阻尼系数cd，质量块的位移量为x，驱动电极上施加的静电，则驱动模态的动力学方程为

(1)

求解输出位移信号

Adsin(ωt-ψd)

(2)

稳态振幅

(3)

稳态相位

(4)

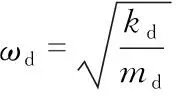
总相移为

ψphase_ref=ψd+ψe

(5)

式中Ψe为电路中元器件的相移，ψd为陀螺工作在谐振频率处的相移，由于温度或者其他环境的影响，驱动模态的谐振频率会发生变化，通过跟踪ψphase_ref能检测信号的变化。ψe可以看作不变的量，只要控制ψphase_ref不变，就能保证陀螺工作在谐振频率处，再用模糊控制保证频率在谐振频率处，能基本保持恒幅振动。

由动力学方程推导：可知位移响应包含了2项之和，前一项是瞬态响应，后一项是稳态响应。可分为振动测试和扫频测试的方法，振动测试是基于时域的测试方法而扫频测试则是基于频域的测试方法。这两种方法可以计算陀螺在谐振频率处的参考幅值和参考相位[7]。

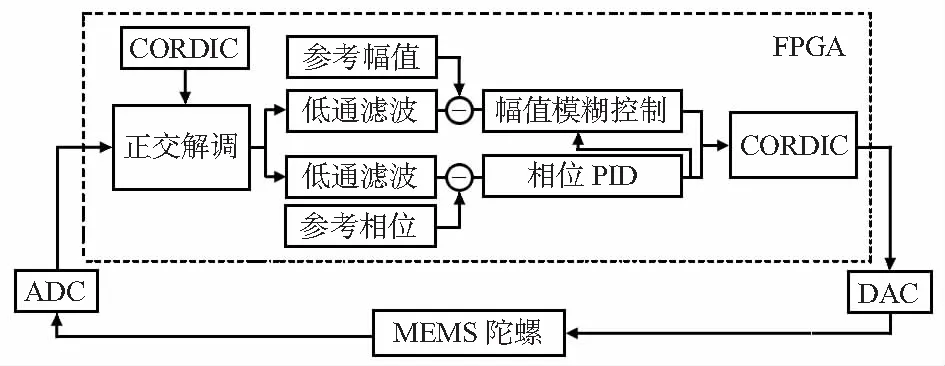
图2 数字闭环驱动示意

2 CORDIC算法原理

CORDIC算法[3]即坐标旋转数字计算方法，主要用于三角函数等的计算，这里通过相位的不断增加逐步计算出相位正余弦，由相位增加的速度(频率控制字)来控制输出频率的大小，提供了驱动信号和解调信号。

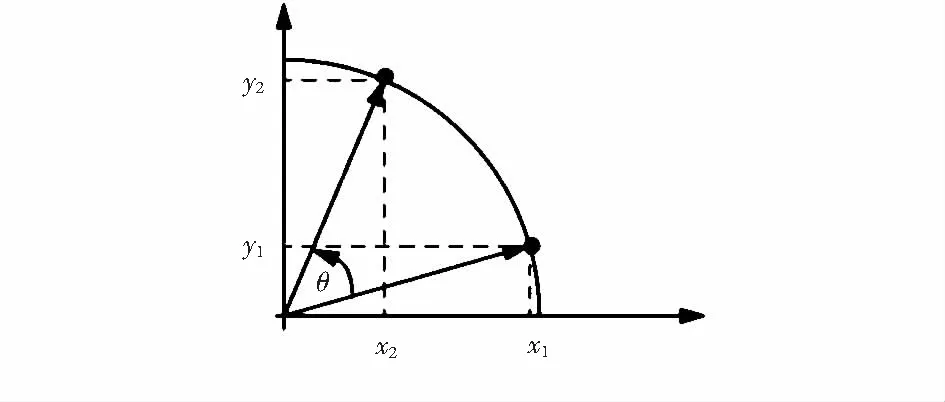
图3 坐标旋转示意

在xy坐标平面上，将点(x1，y1)旋转θ角度到(x2，y2)的标准方法

x2=x1cosθ-y1sinθ,y2=x1sinθ+y1cosθ

(6)

写成矩阵形式

(7)

式中R为旋转矩

(8)

令tanθi=2-i,这样乘正切值变成了移位操作，方便了数字电路的处理。转换因子Ki=(1+2-2i)-1/2得到CORDIC算法的一般表达式

(9)

这里引入第三个方程，称为角度累加器，用来在每次迭代过程中追踪累加的旋转角度。在FPGA中使用了高速全流水线结构的方式，通过基本的加减法和移位运算代替了乘法运算，再使用迭代的方法不断计算所给及的角度的正弦和余弦值。

3 正交解调推导

闭环控制的目的是为了给驱动模态一个恒定的正弦波。正交解调[10]是分离幅值和相位信息，使其能得到有效的控制。假设ADC采集到的信号是A·sin(ωnt+ψ)，再由CORDIC模块产生和采集信号频率一样的正交解调信号sinωnt和cosωnt。频率确定就可以求解幅值和相位。解调过程如下

sI(t)=A·sin(ωnt+ψ)·cosωnt

sQ(t)=A·sin(ωnt+ψ)·sinωnt

(10)

经过低通滤波器滤除的高频信号2ωn，结果为

(11)

经过正交解调可以求得幅值和相位，方便后面的比例积分微分(proportion-integration-differentiation,PID)调节和Fuzzy控制算法的调节

(12)

4 模糊控制算法

模糊控制是一种非线性控制[11]，据模糊控制器设计的理论可知，模糊控制系统的设计中所选的模糊控制器的维数越高，系统的控制精度也就越高，在建立模糊控制规则时就变的比较困难，同时计算机实现起来也比较麻烦。因此，本文主要采用设计的通用方法，采用双输入单输出的二维模糊控制器的设计，如图4所示。

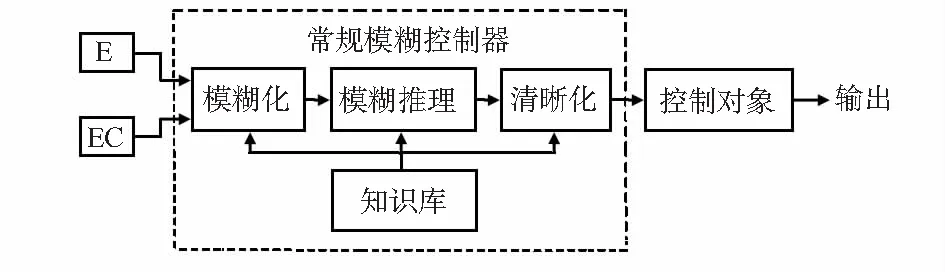
图4 常规模糊控制器结构

模糊语言变量用5个元素的集合(X,T(X),U,G,M)表示，其中，X为语言变量名；T(X)为语言变量名的集合， 且每个值都在U上定义的模糊数Xi；U为语言变量X的论域；G为产生X数值名的语言值规则，是用于产生语言变量值的；M为与每个语言变量含义相联系的算法规则。如图5所示。

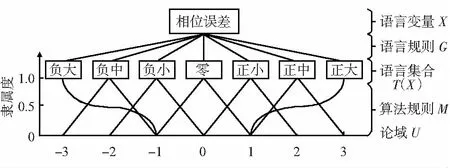
图5 隶属度函数

根据模糊控制结构图可知，模糊控制主要分为三部分：模糊化、模糊推理、清晰化。

4.1 模糊化

输入和输出变量E,EC和ΔVn的模糊子集均为{nb，nm，ns，ze，ps，pm，pb}，即为{负大，负中，负小，零，正小，正中，正大}，它们量化的论域取[-3,3]，取7个模糊档{-3，-2，-1,0,1,2,3}，这个量化的过程就是将E,EC模糊化。由于是需要将ΔVn存入内存中，通过查找表的地址来读取ΔVn的值，在内存中分别用4位二进制表示E和EC，对地址进行编码的主要由两部分组成,分别为E和EC。

4.2 模糊推理

E和EC分别有7个模糊子集，即有了49条规则。模糊规则表是模糊控制器的核心，根据人的经验去设计。其中核心的思想在于：判断E和EC属于哪个论域，来调整ΔVn来快速降低误差。如果E为pb并且EC也为pb时，则ΔVn为nb，其它的设置类似。根据模糊规则表和Mamdani算法，可由式(13)计算控制表

(13)

E'和EC'为普通输入变量,Ei，ECi和ΔVni是模糊规则中的49条规则。最后，用重心法去模糊化，将模糊控制器的输出ΔV'n转化成量化ΔVn。

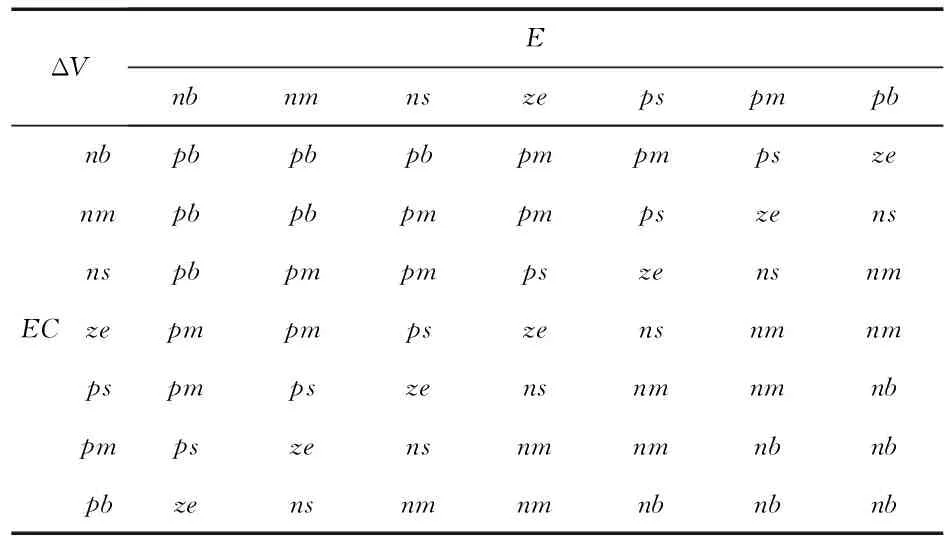
表1 模糊规则表

4.3 清晰化

在整个控制过程中，模糊控制表可以使用MATLAB中的模糊(fuzzy)工具可以方便的求得ΔVn的值，再作为LUT存储于FPGA硬件中。但FPGA的查找表中不能存储小数，可以乘2n(即向左n位)变为整数再存储在查找表中，输出时再除2n还原。

传统的二维模糊控制算法可以描述为

Vn=Vn-1+ΔVn=Vn-1+fuzzy(kpE,kdEC)

(14)

式中E和EC分别为最近一次的控制误差和控制误差变化率ΔVn，kp和kd分别为权重因子，相位控制增量主要由Fuzzy控制器决定[9]。由于缺乏积分环节，为消除静差，提高控制器精度，提出改进的方法

Vn=Vn-1+ΔVn=Vn-1+fuzzy(kpE,kdEC)+kiE

(15)

改进后模糊控制是传统模糊控制和PID的结合体，对控制对象有较高的控制精度。

5 实验结果

实验使用的陀螺是由北京大学自主设计的采用双解耦结构，Q值(标度因子)980,谐振频率9 432.12 Hz。

图6是驱动模态质量块恒幅振动下测试1 h的幅值。振幅的有效值约为0.812 46 V。

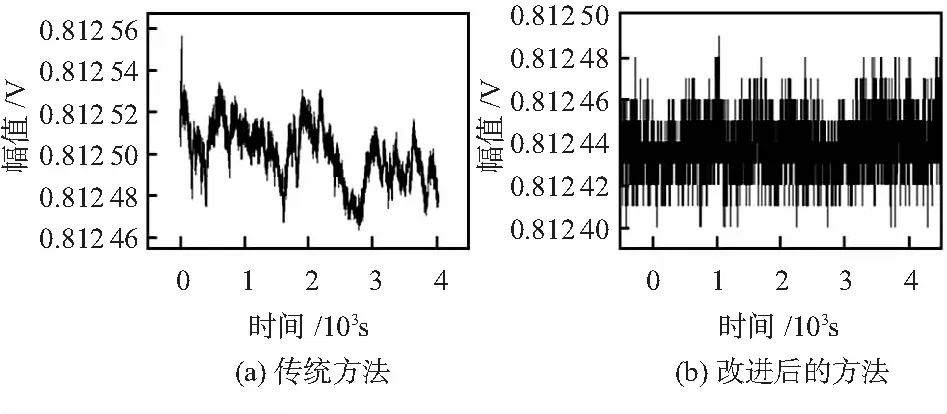
图6 改进前与改进后的模糊控制器幅值变化

图6(a)由于缺少积分环节，无法消除控制器的静态误差，随着时间的变化幅值变化很明显，波动幅度为62 μV，驱动幅值抖动精度为76×10-6。图6(b)是改进的模糊控制器实验结果。

新的控制器加入了积分环节，能有效地消除陀螺静态误差，波动幅度42 μV，驱动幅值抖动精度51×10-6。获得较快的控制能力、较高的控制精度以及较强的鲁棒性。

6 结 论

本文提出一种基于模糊控制算法的MEMS陀螺驱动闭环设计方法，并应用于FPGA平台上。区别于经典PID控制理论,该方法则是基于人类的经验设计而成，属于智能控制方法的一种，具有非线性系统的控制能力。模糊控制器可以通过对陀螺幅值的控制，从而使陀螺保持在谐振状态下，获得恒定幅值和较高的信噪比。