基于深度滤波器优化的SLAM单目稠密重建*
杨海清, 曾俊飞
(浙江工业大学 信息工程学院, 浙江 杭州 310000)
0 引 言
同时定位与地图构建(simultaneous localization and mapping,SLAM)指搭载特定传感器的主体,在没有先验环境信息条件下,通过自身运动的过程来建立所处环境的空间模型,同时估计自身的运动轨迹。当传感器为相机时,称之为“视觉SLAM”。根据使用视觉传感器的数量和类型的不同,视觉 SLAM 系统主要可分为3 类:单目视觉SLAM、多目视觉SLAM和RGB-D SLAM[1]。
重建稠密地图是视觉SLAM的两大目标之一,使用RGB-D相机进行地图重建是目前的主流方法[2],但是RGB-D相机存在测量范围窄、噪声大、视野小、易受日光干扰等诸多问题,主要适用于室内环境。而双目相机的配置与标定较为复杂,其深度量程和精度受双目相机的基线与分辨率所限。对此,本研究选用单目相机传感器,其结构简单,成本较低,环境适应性较强,且抗干扰能力显著。当单目相机移动时图像会形成视差,利用视差可获取像素的深度信息[3]。因此,SLAM系统使用了一种既节省计算量还可使估计的地图点更为准确的方法——深度滤波,通过深度滤波可计算出真实地图点最有可能存在的坐标位置[4]。
无论哪种工业机器人,想要完成准确跟踪定位、精确导航、实时避障和完美还原三维场景的任务,都需有高精度的稠密地图[5]。但是,由于单目相机图像像素可能出现误匹配,且传感器噪声和环境噪声时刻存在,总是会形成一些误差极大甚至假的地图点,导致稠密地图重建准确率不高。因此,为提高单目相机恢复原始场景的能力,本文提出了一种基于深度滤波器优化的稠密重建算法,旨在获取重建准确率更高、表面更加细腻的三维稠密地图。
1 地图重建系统的总体框架
系统的框架主要由三大部分组成,包括:关键帧选取与匹配像素点对、深度滤波技术和稠密建图。具体模块如图1所示。

图1 地图重建系统总体框架
首先,系统对关键帧数据进行极线搜索,采用像素块匹配策略来提高匹配准确率;其次,利用三角化测量获取像素的深度数据,使用滤波器技术对深度数据进行跟踪并融合,实现高效的场景重建;最后,本文综合考虑因光照、遮挡、运动模糊等原因引起的深度值错误估计,显式处理外点,采用优化后的算法对每一像素点的深度估计值进行监控,及时剔除异常深度值,对深度图中相邻像素深度变化过大的情况进一步判断与处理,保证稠密地图的重建准确性。
2 基于深度滤波技术的稠密重建
2.1 稠密地图前端预处理
重建稠密地图,需估计每一个像素点的深度值,如若利用地图中每个像素点的描述子进行匹配,会在前端阶段占用大量的工作时间,这在实时性要求较高的SLAM系统里是不允许的。因此,采用极线搜索[6]和块匹配技术[7]来确定第一幅图像中像素在其他关键帧的位置,如图2所示。
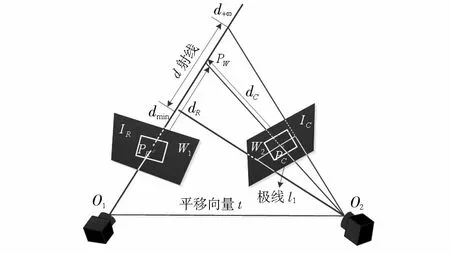
图2 极线搜索示意
左边相机O1观测到参考帧IR存在像素点PR,假设其深度存在的范围区域是最小值dmin到无穷大,即该像素点到对应空间点的距离为图2中的d射线。d射线的投影在当前帧IC上形成一条线,为极线l1,在极线上比较每个像素与PR的相似程度。
本研究采用比较像素块的方法,以提高像素匹配的区分性。先在PR周围选取一个w×w大小矩形窗口W1,再在极线l1上取多个同样大小的矩阵块进行比较,把PR周围的矩形窗口记为W1∈Rw×w,极线l1上的n个小块记为Wi∈Rw×w(i=1,2,…,n)。计算矩形窗口W1与Wi的相似性,采用去均值的NCC方法[8],即
S(W1,Wi)=
(1)
式(1)的结果接近于0时表示两个矩阵块不相似,接近于1则代表相似。
此外,利用仿射矩阵获取到更佳的像素匹配结果[9],并由像素匹配点对估计出当前帧像素深度值,定义为
dRPR=dCRPC+t
(2)
式中R为旋转矩阵,t为平移向量。式(2)两端同时左乘PR的反对称矩阵M可求得当前帧像素深度dC。
2.2 基于均匀—高斯滤波的稠密重建算法
前端预处理阶段提供深度初值,后端滤波器负责对这些数据进行深度融合。均匀—高斯滤波算法[10]采用高斯滤波[11]跟均匀滤波相结合的方法,对同一空间点投射在不同关键帧的像素点深度值进行概率统计分析,不断融合更新深度图。如图3所示。

图3 深度图融合更新过程
图3中,Zk-1是k-1时刻状态的深度值,dk是k时刻的深度估计值。以此类推,可以获取k+n时刻状态的深度值。均匀—高斯滤波器算法模型如下
(1-p)u(μobs|μmin,μmax)
(3)

记均匀分布中上一个状态的参数为aest,best,由新的观测数据计算得到的参数为a,b。经过融合更新后的深度值和方差为μupdate,σupdate,均匀分布的参数变为aupdate和bupdate。深度融合过程如下
(4)
计算权重系数C1,C2
(5)
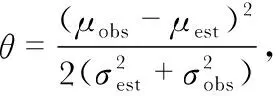
计算U1,U2来更新均匀分布的系数a,b
(6)
进而,深度融合后的均匀分布系数分别为
(7)
融合后像素点的深度值为
μupdate=C′1*m+C′2*μest
(8)
融合后深度值的方差为
(9)

随着深度的融合,像素深度值方差逐渐收敛,当方差保持收敛不变时,则停止对该像素点更新融合,并将深度值记录为真实值。反之,如果深度值的方差经过若干次融合后反而变大,则判断该像素点为外点,将其剔除,并停止更新融合。当所有像素点停止融合时,算法完成场景的稠密重建工作。
3 基于簇的均匀—高斯滤波算法改进
均匀—高斯滤波算法对图像各像素点独立计算深度值,由于像素匹配多义性、噪声等问题的存在,造成相邻像素深度相差过大,算法在遇到弱纹理、倾斜表面等区域时,场景的重建完整性仍存在问题。本文算法对均匀—高斯滤波算法进行改进,在正确处理外点的基础上,构建了用于深度值优化的聚簇分类,簇结构可表征场景的空间平面几何关系,在簇内进行深度值优化可更好重现场景的三维结构。
3.1 簇类划分
均匀—高斯算法实时更新深度图,使用簇类划分对每个时刻更新的深度图进行跟踪,将具有相似特性的区域划分为同一个簇,在簇内对深度值进行优化处理。基于簇的深度更新流程如图4所示。

图4 基于簇的深度更新流程
将深度图均分为400个区域,区域中心像素作为初始种子点,筛选种子点的条件为
λσi<σ
(10)
式中σ为所有像素的深度方差,σi为第i区域内像素的深度方差,λ为自适应阈值,由σ的大小情况而决定。
将筛选后的种子点深度值作为初始均值向量μ={μ1,μ2,…,μi,…,μN}其中N为筛选后的种子总个数。根据划分规则将像素xi划入相应的簇C={C1,C2,…,Ci,…,CN},簇类划分规则定义为
(11)
式中μi为第i个簇的深度均值,xμ为第i个簇中心像素的位置,di为第i个像素的深度值,xi为对应的像素位置。T1为像素距离阈值,T2为深度阈值。将满足式(11)的像素落入相应的簇,未落入任何簇的像素标记为外点,并剔除外点此次状态深度值。
所有像素划分完成后重新计算簇的深度均值,定义为
(12)
式中d为像素深度,|Ci|为簇Ci内像素总个数。更新当前均值向量和簇的中心像素位置后,重复执行上述过程,直至所有簇更新很小甚至不再更新或者达到最大迭代次数,则终止迭代,进而得到簇划分。
3.2 簇内优化
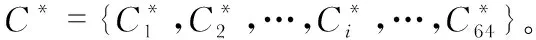
簇内优化算法如下:
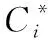
2)若选取的圆上有连续12个像素点深度大于du+T3或者小于du-T3(实验中阈值T3设置为du的10 %),则以该像素点为圆心,选取半径为1个像素大小的圆上的8个像素点;
3)将圆上的8个像素点深度均值作为像素点u的深度值,若像素点u为边缘像素或者圆内包含其他簇的像素时,则对像素点u的深度值不进行处理;
4)循环执行以上三步,对图像中每一个像素执行相同的操作。
深度校准示意图如图5所示。

图5 深度校准示意
故此,采用改进的均匀—高斯滤波算法观测每一时刻的深度图,为后续的深度融合提供精确的深度值,极大避免了像素匹配错误、深度值估计错误所带来的误差,使得重建的稠密地图更加平滑细致。
4 实验结果与分析
为了验证本文算法的有效性和可行性,实验中使用了公共图像帧数据集进行测试。测试数据集包含Remode数据集、Valbonne数据集和Wadham数据集[12],三个公共数据集的真实场景图像如图6所示。实验环境为:Intel 八核计算机,8 GB内存,Windows 64操作系统;算法在Ubuntu14.04系统[13]中进行实现,采用了C++语言和Opencv库[14]。

图6 公共数据集原图
本文分别采用高斯滤波器、均匀—高斯滤波器和改进型高斯滤波器三种深度滤波算法对测试数据集进行试验来获取评测数据,评测指标包括地图的重建情况和重建准确率。实验结果如图7所示。

图7 稠密重建地图
Valbonne数据集背景为天空,深度距离较远,Wadham数据集建筑物包含大量细节,各细节深度相差较小,这些图像特点都会对深度估计造成影响。由图7(a)可知,高斯滤波器对三个数据集的深度估计大致正确,但也存在较多的错误估计,其表现为地图中很多像素点与周围像素点深度不一致,而位于边缘区域的深度也没有得到正确估计。均匀—高斯滤波器将内点和外点进行区别处理,正确处理错误匹配的像素点,图7(b)的三张地图相比图7(a)更为平滑,但在物体与天空的边缘区域仍存在较多地错误估计。从图7(c)中可以明显看出,改进型算法对三个数据集的物体边缘区域进行正确处理,剔除错误估计的深度数据后,重建的稠密地图比其他两种滤波算法重建的地图更加符合实际的三维场景。
将重建的稠密地图与原图进行比对,获取重建后的有效特征匹配对。各测试数据集在各算法上的平均有效特征匹配对如表1和图8所示。图8中的1,2,3分别表示基于改进型均匀—高斯滤波器、均匀—高斯滤波器以及高斯滤波器的特征匹配对数量。

图8 改进型均匀—高斯算法重建的稠密地图有效特征点相对于其他算法的增长比例
由表1数据和图8可知,改进型均匀—高斯算法重建的稠密地图有效特征点大幅增加,稠密度增高,原算法中存在空洞的区域在算法改进后空洞变小。

表1 不同算法的特征匹配对数量对比
为了进一步衡量本文算法的有效性,需定量比较三种滤波算法的重建准确率[15]。记重建准确率为R,参考帧及其相邻的K-1个关键帧为Ci(i=1,2,…,k),关键帧的全部像素点集合为P,关键帧中某一像素点u(u∈P)对应的实际深度值记为Z(u,Ci),由滤波器估计得到的深度值记为Zest(u,Ci)。当像素点u在N个相邻关键帧中都符合这个条件,则认为像素点u的深度值估计成功。故准确率R可定义为
(13)
式中 函数f在括号内条件为真时为1,反之为0,μ为深度值差异阈值,实验中N设置为6。重建准确率对比情况如表2所示。

表2 稠密重建准确率比较
从表2可以看出,本文提出的改进型均匀—高斯滤波器算法在三个测试数据集上的稠密地图重建准确率分别为0.836 2,0.803 4和0.843 7,各个数据集的重建准确率相比于高斯滤波和均匀—高斯滤波这两种深度滤波方式分别提高了约30 %和10 %。显然,改进型算法无论是在室内场景还是在复杂环境的室外场景,都表现出较强的深度滤波能力,说明该算法在单目稠密重建地图方面有着较显著的有效性和较高的准确性。
5 结束语
稠密建图是视觉SLAM的主流建图方式之一,其广泛应用于各项工业任务中。针对高斯滤波算法重建稠密地图存在像素点误匹配、重建准确率不高的问题,本文提出了一种基于簇的均匀—高斯深度滤波算法,将深度估计值从一个非常不确定的值逐渐逼近到一个稳定值,重建出更加准确的三维稠密地图。实验结果表明,本文算法在不同环境下的数据集中都表现出较强的适应性,能较好地处理弱纹理区域、光照遮挡区域和弧面区域中存在的深度错误估计问题,并实时剔除外点数据,优化簇内深度值数据,在三个数据集上的重建准确率都高于高斯滤波算法和均匀—高斯滤波算法,重建的稠密地图也比其他两种算法更加准确、细致。在下一步工作中,将根据图像颜色分布情况和帧间变换信息,进一步改进复杂环境的深度估计,构建更加完善的稠密地图。

