基于Simulink的等效电路参数辨识研究

林文发 陈德旺 林松青

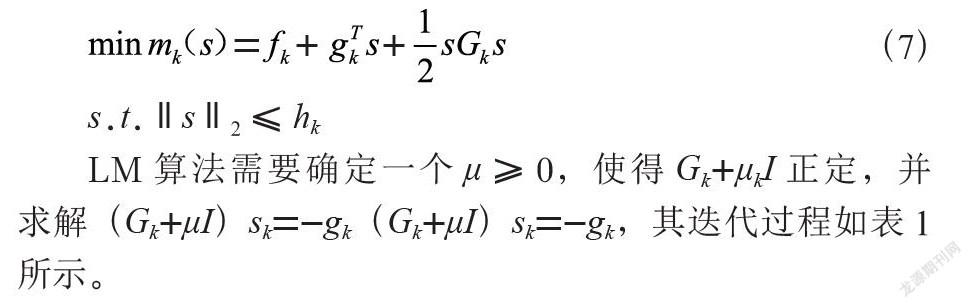
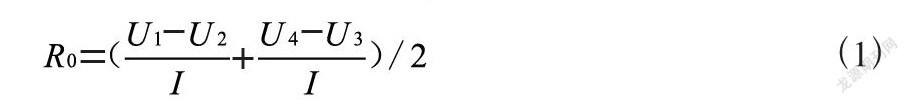
摘  要：动力电池参数辨识是电池测试工作中的重要一环，由于电池内部化学反应复杂，电化学模型和经验模型都无法满足工业测试需求。本文采用RC等效电路建立电池模型，在Simulink平台上搭建电池仿真系统，使用工业测试的脉冲放电数据做训练集和测试集，利用非线性最小二乘法和LM最优化算法估算动力电池的参数。实验结果表明，利用并行计算工具可以提高约34%的计算效率，仿真数据与实验数据均方误差为5.33066×10-3，非线性最小二乘法比Gradient Descent算法更适用于电池参数辨识，模型精度高，该模型可以用于动力电池的测试与开发。

关键词：动力电池;等效电路模型;非线性最小二乘法;LM算法

中图分类号：TM134;TM912      文献标识码：A 文章编号：2096-4706（2019）24-0023-05

Abstract：Power battery parameter identification is an important part of battery testing. Due to the complex internal chemical reaction of the battery，electrochemical models and empirical models cannot meet the industrial testing requirements. In this paper，the RC equivalent circuit is used to build the battery model. The battery simulation system is built on the Simulink platform. The industrial test pulse discharge data is used as the training set and test set. The nonlinear least squares method and the LM optimization algorithm are used to estimate the parameters of the power battery. The experimental results show that the parallel computing tool can improve the computing efficiency by about 34%，and the mean square error of simulation data and experimental data is 5.33066×10-3. The nonlinear least square method is more suitable for the identification of battery parameters than the Gradient Descent algorithm，and the model accuracy is high. The model can be used for the test and development of power battery.

Keywords：power battery;equivalent circuit model;nonlinear least squares;LM algorithm

0  引  言

目前人類社会已经是一个电力社会，电力设施分布密度极高。锂电池作为绿色新能源，因其具有工作电压高、比容量大、能量密度大、循环寿命长、自放电率小、清洁无污染、电流效率高等独特优势而在电动车行业广受青睐[1]。在现代工业采取的电气功能测试中，实时HIL（硬件在环，Hardware-in-the-Loop）系统环境对系统仿真的速度以及精确度要求严格。然而电池本身是一个复杂的系统，受外界的影响很大，电池的内部电化学反应十分复杂。同时电池自身的性能具有多变性，在不同条件下的充放电过程中，表现出的差异也比较明显[2]。由于电池的运行受到外部环境的影响特别大，增加了HIL系统仿真的复杂性，如何有效地进行锂电池参数识别成为电池建模的研究热点。

目前，动力电池模型的研究主要分为三类：电化学机理模型、经验模型和等效电路模型。一些早期的研究者建立了电化学机理模型，但电化学机理模型通过电化学反应第一性原理，以偏微分方程描述电化学动力学过程，含有大量先验电化学参数，计算复杂，不具备通用性[3]。而一些基于神经网络的经验模型无法对映射关系进行机理性解释，且模型参数选择通常无定性规则可供参考。模型预测精度与训练集范围密切相关，因此，在实际应用中存在一定局限性[4]。本文采用了等效电路模型进行研究，利用工业测试数据做训练集和测试集，使用Simulink搭建电池的等效电路模型，不仅能够直观上表征电池的内部特征，而且能够与机器学习等智能算法灵活结合。在电池参数辨识阶段，使用了并行计算工具，提高了参数辨识的效率。本文将从以下四个内容展开：第1部分实验数据的分析、第2部分电池模型的搭建、第3部分电池参数估算流程、第4部分实验结果及分析，并在最后对全文进行总结。

1  实验数据的分析

HPPC（混合动力脉冲能力特性，Hybrid Pulse Power Characteristic）是用来体现动力电池脉冲充放电性能的一种特征。HPPC测试一般采用专用电池检测设备完成。进行该放电实验测试，能够获得所测电池的各类动态特性，进而能够方便地获得电池模型的各项参数[5]。

以美国的FreedomCAR的标准测试方法为参考，本次实验采用的HPPC测试具体步骤如下：

步骤1：将锂电池按照1C恒流放电1h，静置0.5h。

步骤2：将锂电池按照1C恒流充电1h，静置0.5h。

步骤3：为了让零输入响应时的极化效果更显著，重复步骤1和2两次，使SOC（锂电池荷电状态，State of Charge）处于SOC=100%的充满状态。

步骤4：将锂电池按照1C恒流放电10s，锂电池按照1C恒流充电10s。

步骤5：将锂电池按照1C恒流放电6min。

步骤6：将锂电池静置1h。

步骤7：重复步骤3、4、5，取SOC点从90%至10%，采样间隔为10%，共9个点为电池的采样点。

步骤8：测试结束。

在HPPC测试的准备阶段，需要对锂电池进行循环充放电数次，以保证HPPC测试数据的准确性，测试结束就能够得到一个完整的HPPC测试数据。通常，在HPPC测试阶段，电池的极化效应显著，表现为电压跃升和突降，直到电池的静置阶段电压才有所恢复。随着放电的深度不断加大，电池的最高电位呈现不断下降的趋势。

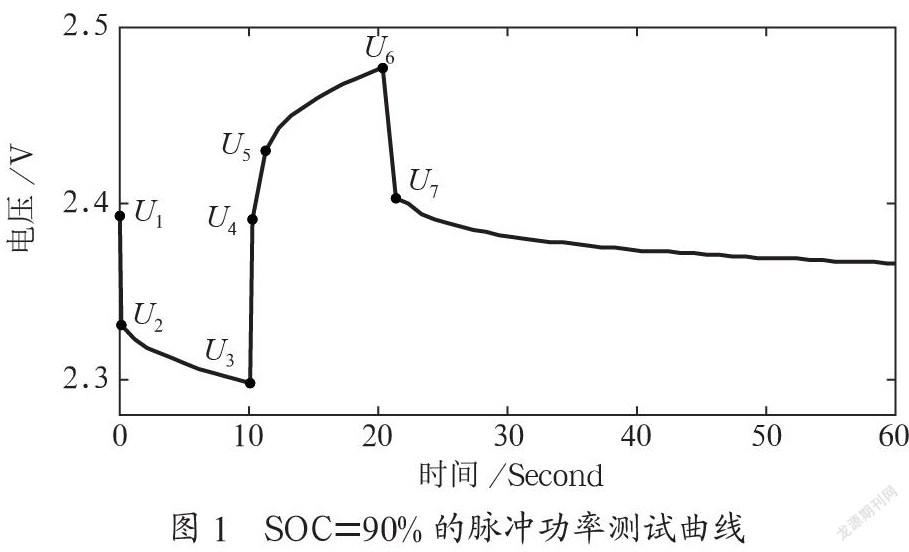
一个完整的HPPC脉冲放电过程包含十次的循环充放电过程，10个充放电过程设置为10个采样点。每个采样点的电化学反应原理一致。所以只需要针对一个SOC采样点上的脉冲功率测试曲线进行数据分析就能理解脉冲放电的全过程。本文选取SOC为90%采样点的电压数据分解如图1所示。

如图1所示，U1—U4为10s的放电脉冲区间：此时电池受到10s的放电脉冲，由于产生了极化现象，电池的电压会迅速从U1下降至U2，产生这部分压降的主要原因是欧姆极化[6]。U2—U3部分可以认为是在持续放电期间电化学极化和浓差极化共同产生的压降。当放电电流消失，电池电压从U3迅速回弹至U4，是由于电池的欧姆极化作用的消失。此时可以得到电池的直流内阻R0的公式：

（1）

其中R0为直流内阻，I为电流，放电过程的压降与充电过程的压升都可以用来求解欧姆电阻，但由于测试过程中存在着误差，所以取两段放电脉冲区间的均值作为欧姆内阻。

U4—U7为10s的充电脉冲区间：与放电同理，在同一SOC状态下，放电和充电的欧姆内阻的RC参数存在一定差异[7]，为了保证模型精度可以分别求出充放电的参数，需要再根据实际电流情况进行参数切换。

2  电池模型的搭建

目前，常见的等效电路模型有Rint、RC、Thevenin、PNGV和GNL模型。Rint模型也称内阻模型，由于该模型没有考虑电池的极化特性，因此模型精度较低[8]。Thevenin模型存在无法线性化的参数，给参数辨识带来了困难[9]。而PNGV和GNL模型的复杂度和辨识难度颇大。

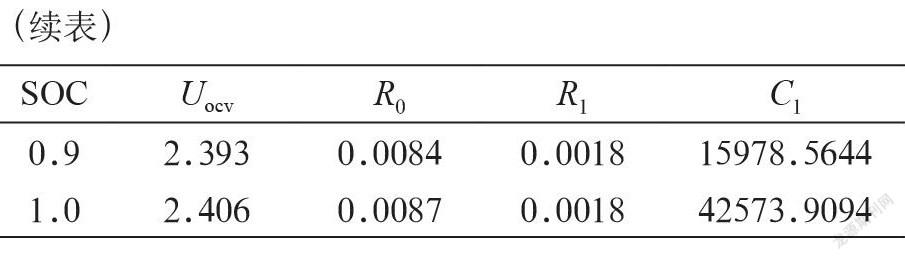
胡晓松等人在比较了十二种常用等效电路模型的复杂性，准确性和鲁棒性三个方面之后得出结论：1-RC等效电路模型具有最优的模型性能[10]。1-RC等效电路模型的结构如图2所示。

其中，电压源Uocv表征电池的开路电压。直流电阻R0表征当电池加上外加负载后端电压的压降特性。串联一串RC电路，C1表示电容，R1表示电阻，用来表征电池时间常数和频率响应等特性。

由于电池内部的电化学效应，存在某些寄生电容或电阻，会引起一些能量损失，但在锂电池的充放电过程中影响很小，为了方便建模仿真，假设先忽略这些因素对电池的影响。

根据1-RC等效电路模型，可以得到电池端电压满足以下公式：

其中SOC为电池的荷电状态，T为电池温度，I为直流电流，V为电池电压，Px（parameter）表示的是锂电池各参数Uocv、R0、R1、C1的其中一个。通过式（6）可以直观地理解为电池参数的辨识，实际上求解电池内部属性与SOC、温度等输入参数之间的关系。

根据建立的1-RC等效电路模型，本文采用MATLAB工具的Simulink平台搭建对应的电池模型。Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。

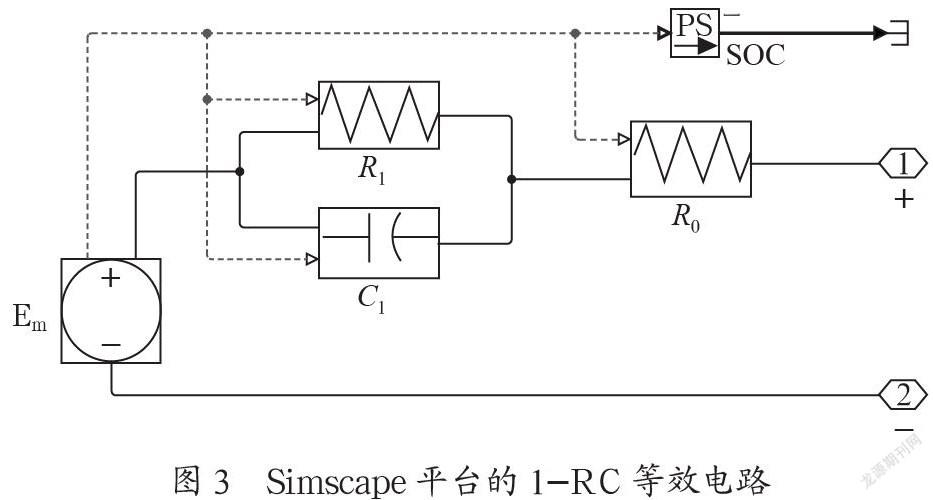
Simulink的Simscape基础模块，可以实现多领域物理建模。打开Simulink的Libraries，然后打开Simscape的Electrical和Thermal模块，选择正确的元器件，搭建的1- RC等效电路模型如图3所示。

从图3可以直观看出Simscape搭建的电池模型与设计的1-RC等效电路结构一致，元器件之间的连接符合物理学电路原理。将图3的1-RC等效电路作为整个仿真系统的子模块，并连接好正确的电池元器件，设置好电流和电压的输入输出，以及各自的示波器，就可以使用测试数据对等效电路模型的参数进行估算。

3  电池参数估算流程

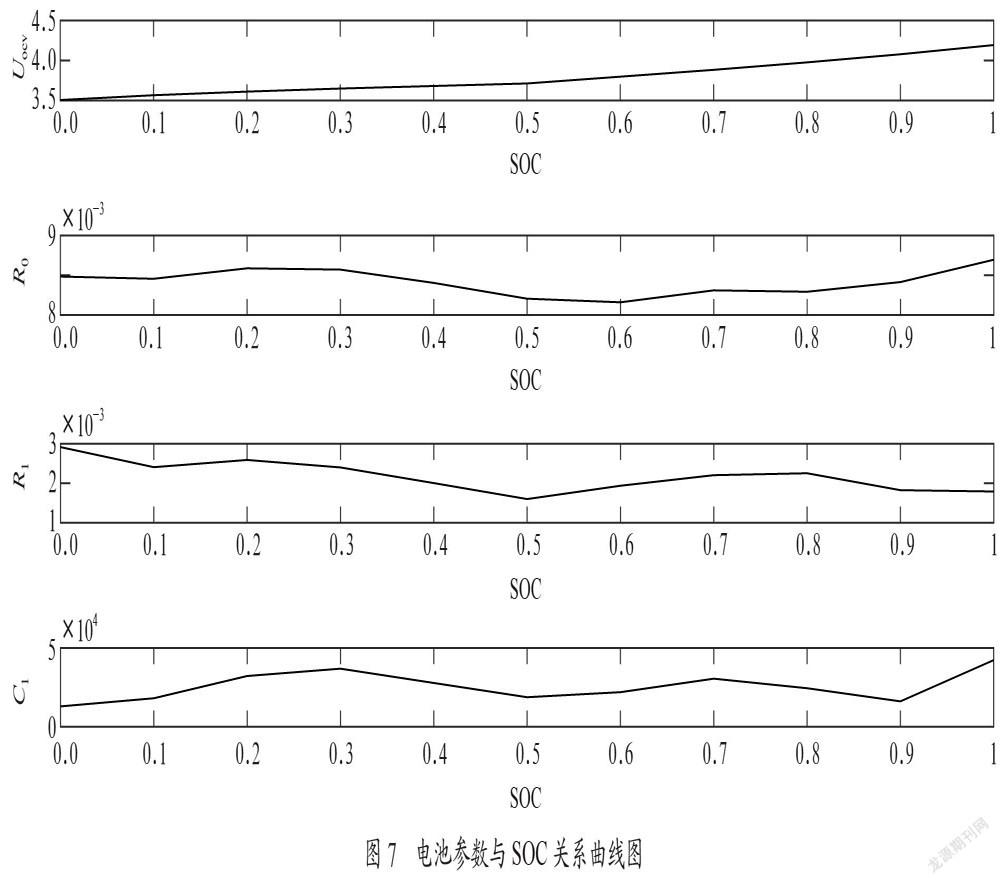
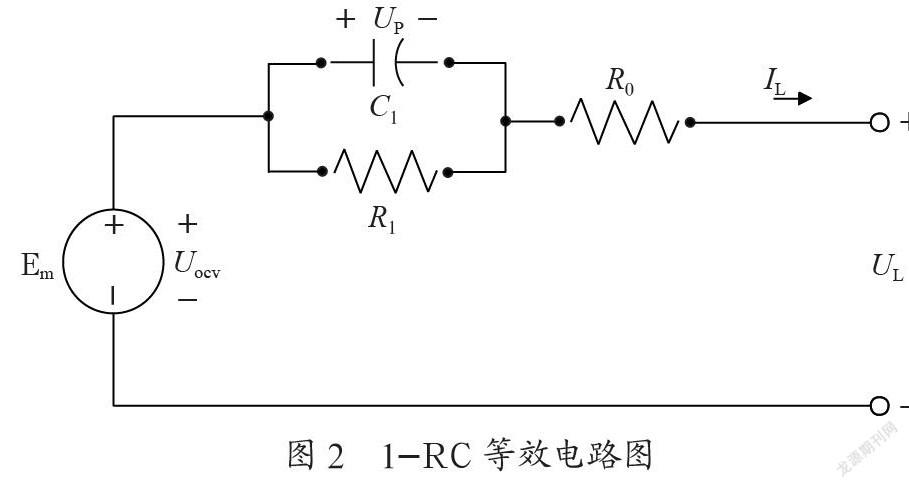
本文通过脉冲放电实验产生的数据对搭建的Simulink电池模型进行参数辨识，首先需要进行电池参数的初始化。对实验环境为恒温（24℃）条件下的电池做仿真，所以温度T为常数，SOC的值设置为0≤SOC≤1，步长为0.1，电容C1初始值为1000F，电阻R0初始值为0.01Ω，电阻R1初始值为0.05Ω，开路电压Uocv初始值为1V。

为了简化系统的仿真，暂时先忽略電池的热效应及寿命老化引起的电池内部参数的变化，则锂电池参数估算的流程如图4所示。

本文使用Simulink的Parameter Estimation工具箱进行参数辨识，先将处理好的10个采样点的HPPC脉冲放电数据作为训练集导入模型，设置好参数估算的迭代次数，并进行参数初始化操作。调用工具箱的非线性最小二乘法（Nonlinear Least Squares）求最优解，采用信赖域LM最优化算法。其数学模型如下：

在LM算法求解的过程中需要求解线性方程组，一般使用较稳定的高斯-若尔当消元法（Gauss-Jordan）。

在设置好参数迭代次数、调整好算法之后，就可以进行参数辨识，为了更直观地观测实验的结果，需要在迭代过程中，绘制迭代过程的误差曲线图以供后续分析。

同时，由于迭代的次数较大，系统运行的时间较长。为了提高效率，可以使用并行计算工具Parallel Computing Toolbox，系统会自动分配分布式计算的内核数，进行资源调度，以提高计算效率。

4  实验结果及分析

为了验证采用算法的合理性，在使用非线性最小二乘法的同时，使用梯度下降算法（Gradient Descent）进行两者的实验结果对比。两种算法在迭代过程中产生的SSE（和方差，The Sum of Squares due to error）曲线如图5所示。

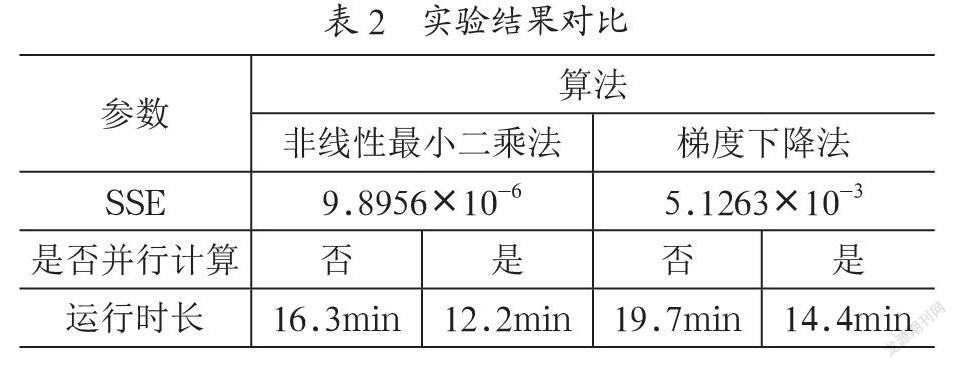
从图5可以得出，非线性最小二乘法收敛更快，说明其更适用于锂电池参数的辨识。非线性最小二乘法的迭代误差不断减小，随着迭代次数的增加，逐渐趋于平缓，收敛并趋于0，验证了算法的正确性。通过算法的不断迭代，非线性最小二乘法估算的和方差逐渐收敛趋于0，说明搭建的Simulink电池模型有较高的精度，能够较好地拟合实验数据，本次实验的最终SSE误差为9.8956×10-6。为了分析并行计算的优势，还分别对两种算法在有无并行工具的情况下进行了实验，如表2所示。

从表2可以得出，在锂电池的参数估算实验中，非线性最小二乘法比梯度下降法更有优势，使用并行计算工具能够使计算效率大约提高34%。

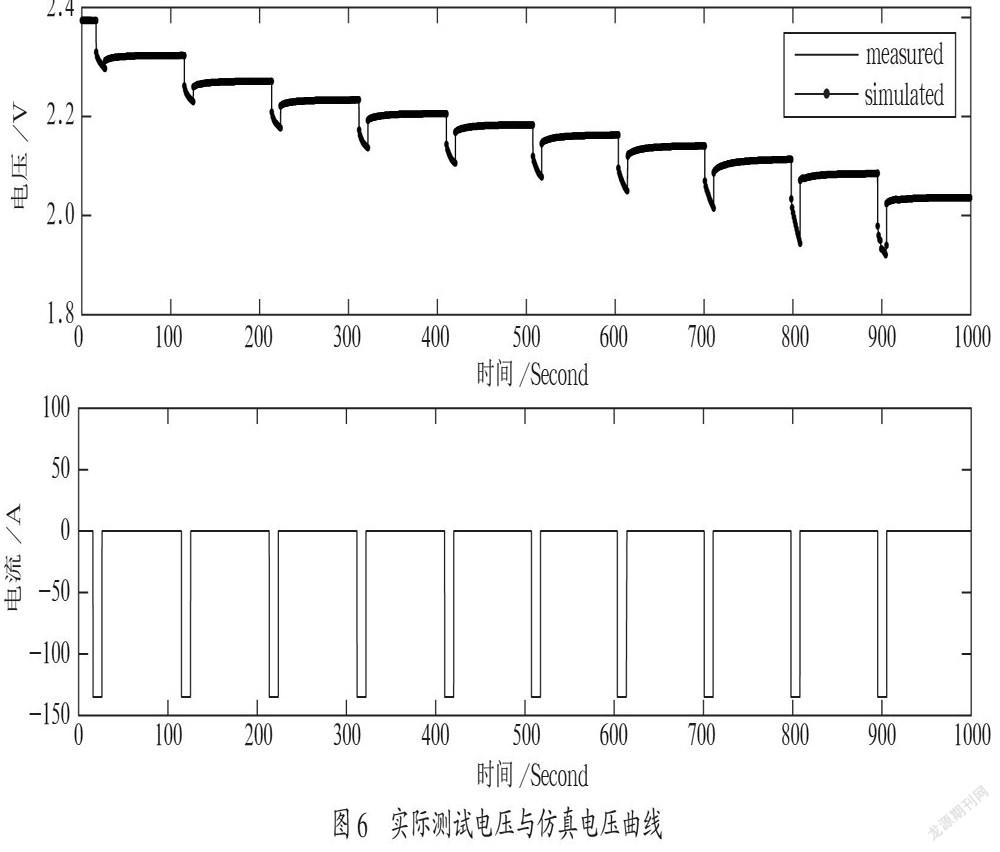
为了验证仿真的Simulink等效電路模型具有较高精度，采用另一组电池的HPPC脉冲放电数据作为测试集，对模型进行验证和评估，并绘制仿真与测试实验的数据曲线图以供对比分析，如图6所示。

从图6可以看出，当电池以150A脉冲放电时，电池的最高电位会随着SOC的递减而逐渐下降。除了在极化效应显著的一些跳跃点，实验电压数据曲线和仿真数据曲线几乎一致，从图形上直观体现了仿真模型的高精确性。

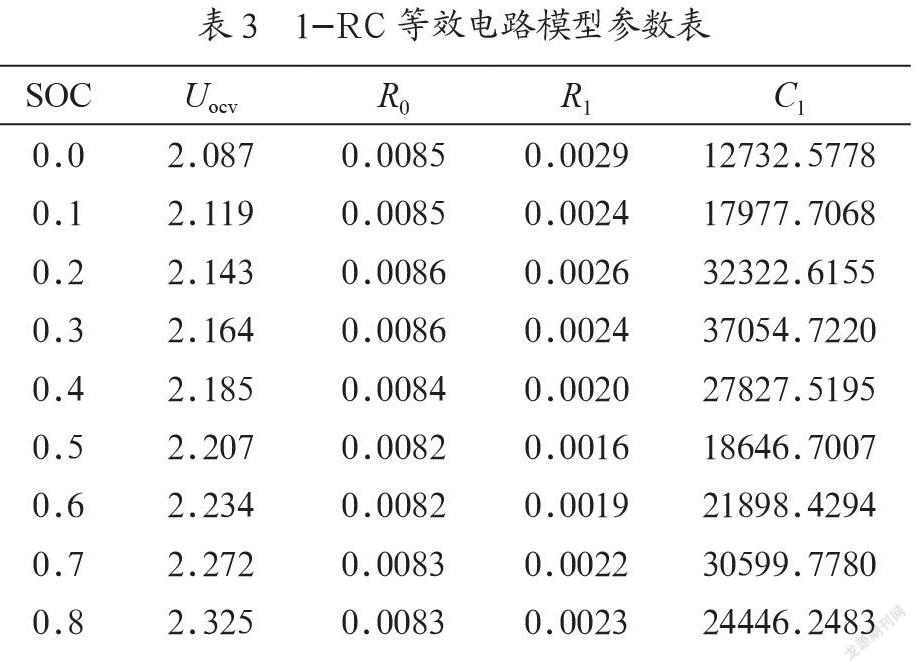
从图7中可以看出Uocv与SOC的曲线大致呈直线型，说明二者存在着较强的正相关的线性关系，符合现实情况。在进行更复杂的电池设计时，可以考虑用简单的线性方程表征二者之间的关系。电阻R0、R1与SOC的关系曲线相对比较平缓，但在两端变化稍微较大。尤其是SOC=0.1附近，在该段范围内，由于电池的热效应等，电压突降，对参数影响巨大，通常工业上将SOC=16.25%的点设置为下限预警点。所以，在对R0，R1进行拟合时，可以考虑使用分段函数，跳变的前后的两端用不同的方程来表征。C1与SOC的关系最为复杂，曲线呈现出陡变的锯齿形，难以用线性方程来拟合，可以考虑使用神经网络等算法来进行处理。

5  结  论

由于动力电池是一个复杂的系统，电化学模型和经验模型无法满足日益严格的电气功能测试需求。本文分析了脉冲放电的过程及电池内部的反应原理，采用了电路相对灵活、结构简单、便于建模的等效电路模型，并对电路的基本电化学反应进行了数学分析。以此为基础，本文使用了Simscape平台搭建对应的1-RC等效电路模型，设计了电池参数辨识的具体方案，利用非线性最小二乘法和LM算法对模型的参数进行辨识，并使用并行计算工具提高了计算的效率。实验的结果表明，搭建的等效电路模型精度较高，误差较小，能够很好地拟合测试数据，满足工业测试规定的标准，非线性最小二乘法比梯度下降算法更适合用来做锂电池参数辨识，使用Parallel Computing Toolbox能够提高约34%的计算效率。此外，通过进一步分析电池内部参数的依赖关系，提供了二维查找表，以供后续的SOC预测算法研究参考。

电池内部存在着热效应，复杂的热效应对电池内部的参数影响很大，不同温度下，各参数之间的依赖关系也会有所变化。本文采集到的数据是在室内恒温24℃情况下的锂电池脉冲放电数据，有关不同温度下的动力电池参数辨识是本文接下来进一步研究的工作。

参考文献：

[1] 冯庆娜.浅析新能源汽车 [J].科技经济导刊，2017（14）：126.

[2] 时玮，姜久春，张维戈，等.磷酸铁锂电池并联充放电特性研究 [J].高技术通讯，2012，22（2）：205-210.

[3] 刘伟龙，王丽芳，廖承林，等.充电模态下电动汽车动力电池模型辨识 [J].电工技术学报，2017，32（11）：198-207.

[4] 沈佳妮，贺益君，马紫峰.基于模型的锂离子电池SOC及SOH估计方法研究进展 [J].化工学报，2018，69（1）：309-316.

[5] 姚建光，徐兴春，史慧生，等.基于HPPC实验的铅酸电池的建模技术研究 [J].科技创新与应用，2018（2）：13-14.

[6] 郑英东.三元锂离子电池的SOC估计方法研究 [D].大连：大连理工大学，2015.

[7] 姜威.LiFePO_4动力电池二阶RC模型参数的研究 [D].杭州：浙江大学，2015.

[8] 余文正.动力电池模型分析及其快速充放电策略研究 [D].成都：电子科技大学，2013.

[9] 王世繁，罗杨，董亮，等.二阶Thevenin锂电池等效模型参数离线辨识 [J].电子设计工程，2018，26（9）：46-49+54.

[10] HU X，LI S，PENG H. A comparative study of equivalent circuit models for Li-ion batteries [J].Journal of Power Sources，2012，198：359-367.

作者简介：林文发（1994-），男，汉族，福建三明人，硕士研究生，主要研究方向：智慧新能源、大数据;陈德旺（1976-），男，汉族，安徽南陵人，教授，博士，主要研究方向：交通信息工程及控制、机器学习、智能交通系统;林松青（1977-），男，汉族，福建莆田人，工程师，学士学位，主要研究方向：动力电池软件开发、智慧新能源。