改进布谷鸟搜索算法求解零空闲流水线调度问题

彭勇 郑慧君

摘  要：本文针对零空闲流水线调度问题，提出了一种基于自适应步长和发现概率的改进布谷鸟搜索算法，建立了以工件的最大完工时间为目标的算法模型。最后在若干Taillard Benchmark问题上的仿真实验表明了改进布谷鸟搜索算法解决零空闲流水线调度问题的有效性。

关键词：零空闲流水线调度;布谷鸟算法;最大完工时间;发现概率

中图分类号：TP181;TP301.6      文献标识码：A 文章编号：2096-4706（2019）24-0020-03

Abstract：In this paper，an improved cuckoo search algorithm based on adaptive step size and discovery probability is proposed for no-idle flow shop scheduling，and an algorithm model aiming at the maximum completion time of makespan is established. Finally，simulation experiments on several Taillard Benchmark problems show the effectiveness of the improved cuckoo search algorithm in solving the no-idle flow shop scheduling problem.

Keywords：no-idle flow shop scheduling;cuckoo search;makespan;discovery probability

0  引  言

零空闲流水线调度（No-Idle Flow Shop，NIFS）问题是一类典型的调度问题，不但具有重要的理论价值，而且具有实际意义[1]。文献[2]提出了解决该问题的一种离散果蝇优化算法，文献[3]提出了一种解决NIFS问题的粒子群优化算法。

在基于群体智能的算法中，布谷鸟搜索算法（Cuckoo Search，CS）以较少参数和较好的鲁棒性，成功用于多个领域[4，5]。因而，针对NIFS问题，本文将会在CS的基础上，对其步长、发现概率进行相应的改进，提出一种新的改进布谷鸟搜索算法（Improved Cuckoo Search，ICS），以期能解决NIFS问题。

1  零空闲流水线调度问题的数学模型

零空闲流水线调度问题的一般描述为：n个工件{J1，J2，…，Jn}在m台机器{M1，M2，…，Mm}上进行流水加工，每个工件在机器上的加工顺序相同，每台机器加工的各工件的顺序相同，同时约定每个工件在每台机器上只加工一次，而在同一机器上加工的相邻工件之间没有等待时间，且机器之间存在无限缓冲区。ti，j为工件Ji在机器Mj上的加工时间;Ck，j为在机器Mj上加工的第k个工件的完工时间;R为工件排列形成的序列;并令决策变量为：

约束条件（3）和（4）保证了每个工件都会在排列R中出现且仅出现一次;约束条件（5）给出了第一个加工的工件在第一台机器上的完成时间;约束条件（6）和（7）保证了同一台机器上加工的相邻两工件和间的完工时间的关系，表明了同一时间在同一台机器上只能加工一个工件，同时用等号连接保证了机器上相邻两工序间无时间间隔，即保证了机器的无间断运作。

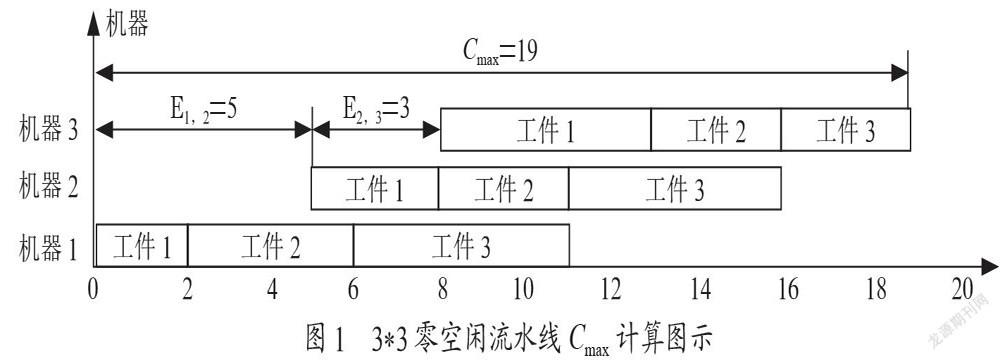
由于零空闲流水线调度问题的机器不允许空闲，其最大完成时间的算法将不同于置换流水线调度问题的算法，研究中引入了一个中间变量——最早开工时间来辅助计算各工件的最大完成时间。

最大完成时间的计算方法：

假设工件加工的顺序为R={R（1），R（2），…，R（n）}，tR（i），j表示R（i）位置上的工件在机器j上的工序作业时间，Ej，j+1为相邻的机器j和j+1之间的开工时间差，那么相邻机器间的开工时间差可按下列公式进行计算：

工序R的最大完成时间的计算过程图如圖1所示。

2  改进布谷鸟搜索算法解决NIFS问题

2.1  标准布谷鸟算法

布谷鸟搜索算法是一种模仿布谷鸟寻觅窝巢产蛋行为的启发式智能优化算法。标准布谷鸟算法主要思想是通过Lévy飞行路径产生候选鸟窝以及采用精英保留策略更新当前鸟窝位置，最终使鸟窝位置能够达到或接近全局最优解。根据文献[6]，布谷鸟寻窝的路径和位置更新公式如下：

在标准的多目标布谷鸟算法中，Lévy飞行的步长控制量∂0为固定值，原种群经连续跳跃，随机游走后得到新种群，然后以发现概率pα放弃一些较差的个体并随机生成新的解来补充到新种群，这样不能保证算法在较低的迭代次数下的收敛性和寻优精度。

2.2  改进布谷鸟搜索算法

由于布谷鸟是采用Lévy飞行模式在搜索空间随机搜索的，其搜索步长和方向都是高度随机的，从一个区域跳跃到另一个区域也是随机的，这种模式对早期的全局寻优搜索无疑是有利的，可以较快接近全局最优解，但随着CS算法多次迭代后，后期全局最优附近的局部寻优会因Lévy飞行模式跳跃性较大，造成鸟巢附近的局部最优信息得不到利用，因而后期收敛速度和精度反而弱化，为提高CS算法的收敛速度和精度，必须随着算法的动态变化而调整步长因子和发现概率[7]。

其中，pi为第i代发现概率，pmin是最小发现概率，pmax是最大发现概率，iter是当前代数、maxiter是最大代数，∂i是第i代步长因子，∂min是最小步长因子，∂max是最长步长因子。

3  仿真实验及结果分析

为了检验改进布谷鸟算法求解零空闲流水线问题的效果，我们采用Taillard Benchmark中的不同规模的算例进行了试验，采用文献[8]提出的遗传算法（GA）以及本文提出的标准布谷鸟算法（CS）和改进布谷鸟算法（ICS）对每个算例仿真5次，计算平均相对偏差（PRD）和平均方差（SD）。

3.1  实验环境

算法采用C++编程实现，测试的平台为Windows 7，机器的主频为3.60GHz，内存为8GB。

3.2  参数设置

设置种群的大小为30，pmin=0.005，pmax=1，iter是当前代数、maxiter=200，∂min=0.05，∂max=0.5。

3.3  结果分析

3.3.1  平均偏差和平均均方差分析

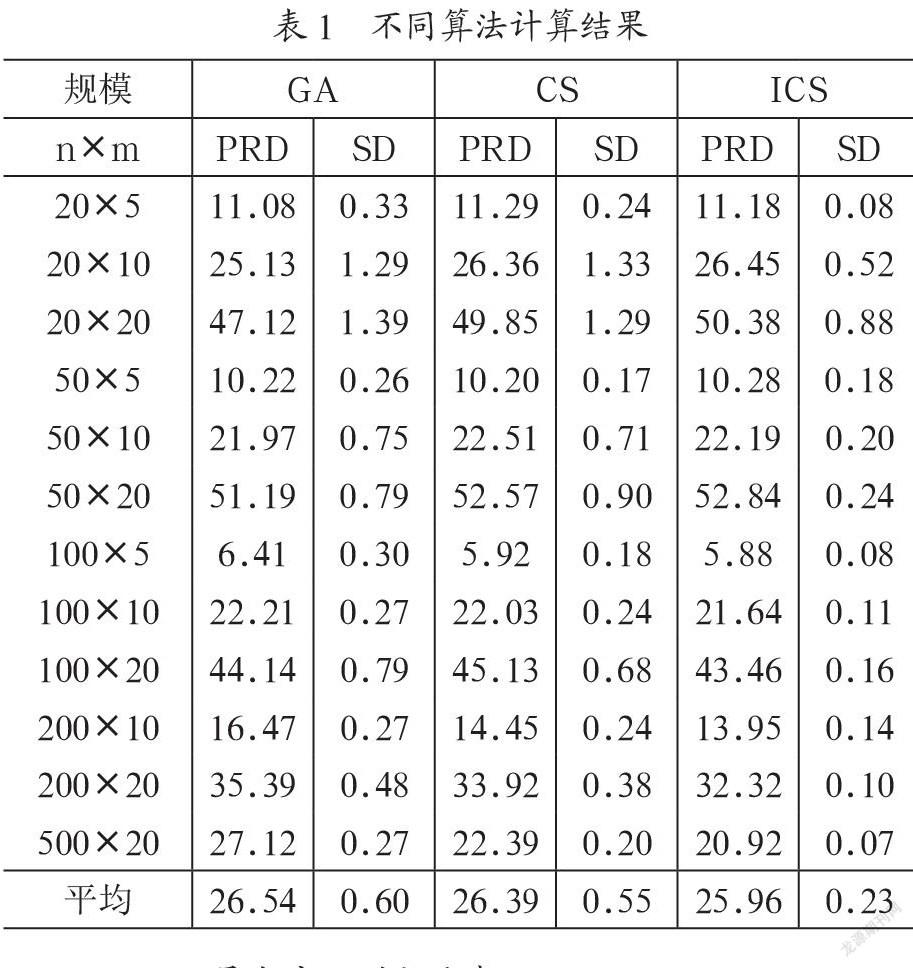
不同算法计算结果如表1所示，从表1可以看出：

（1）CS算法所得的平均偏差和平均均方差略小于GA算法，表明CS算法在解的质量上优于GA算法;

（2）ICS算法所得的平均偏差和平均均方差小于CS算法，表明本文采取的提高算法性能的措施是有效的。

3.3.2  最大完工时间分析

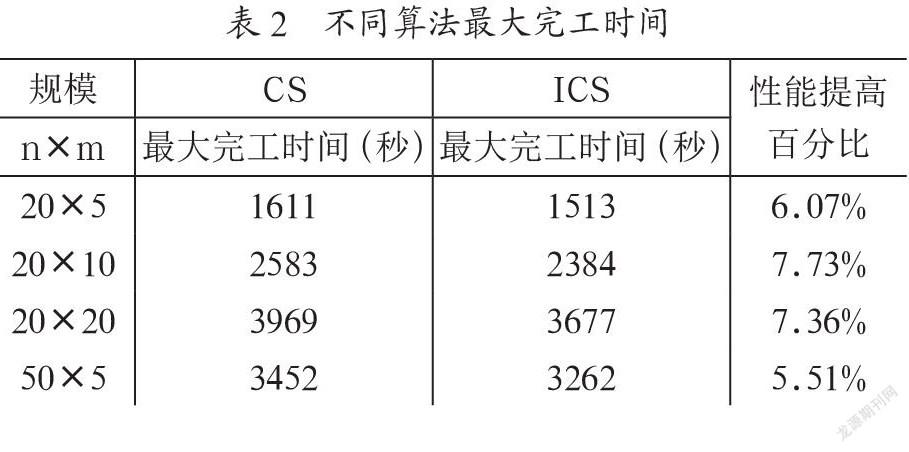
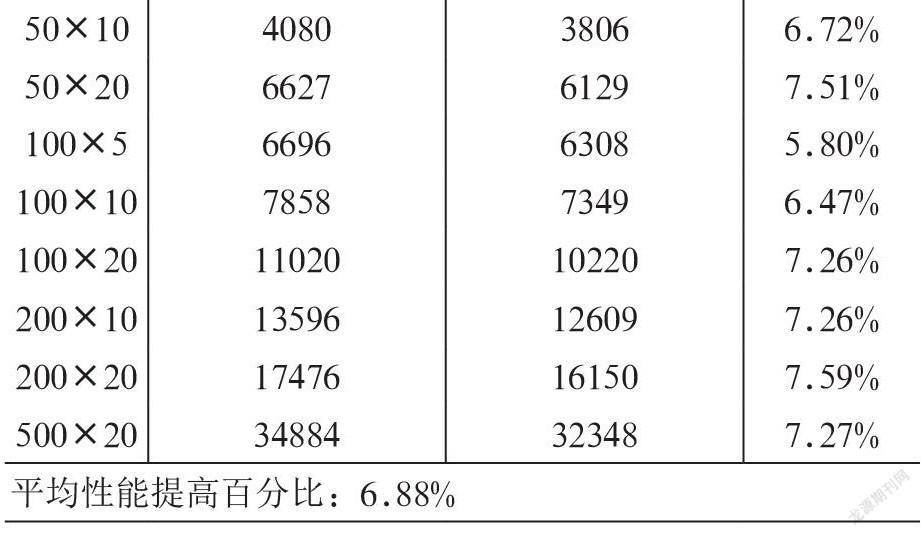
不同算法最大完工时间如表2所示，从表2中可清晰看出，ICS算法得到的不同规模算例的最大完工时间均优于CS算法。在最好情况下，ICS算法性能可提高7.73%，其平均最大完工时间提高了6.88%，说明ICS算法优于CS算法，我们提出的改进是有效的。

4  结  论

本文提出了一种改进布谷鸟算法，该算法采用自适应的步长因子和发现概率，并运用此算法于零空闲流水线调度问题中。仿真实验表明，该算法有助于改善解的质量和提高收敛速度，对解决流水线车间调度及自动化工程等问题具有较高的实用价值。

参考文献：

[1] 齐学梅，王宏涛，杨洁，等.量子萤火虫算法及在无等待流水调度上的应用 [J].信息与控制，2016，45（2）：211-217.

[2] 張其亮，俞祚明.基于优势种群的离散果蝇优化算法求解无等待流水车间调度问题 [J].计算机集成制造系统，2017，23（3）：609-615.

[3] 张其亮，陈永生.求解双向无等待混合流水车间调度问题的粒子群优化算法 [J].计算机集成制造系统，2013，19（10）：2503-2509.

[4] YANG X S，DEB S.Cuckoo search via levy flights [C]//Proceedings of the World Congress on Nature & Biologically Inspired Computing，IEEE Publications，USA，2009：210-214.

[5] 黄辰，费继友，王丽颖，等.基于多策略差分布谷鸟算法的粒子滤波方法 [J].农业机械学报，2018，49（4）：265-272.

[6] 董崇杰，刘毅，彭勇.改进布谷鸟算法在人群疏散多目标优化中的应用 [J].系统仿真学报，2016，28（5）：1063-1069.

[7] LI R Y，DAI R W.Adaptive Step-size Cuckoo Search Algorithm [J]. Computer Science，2017，44（5）：235-240.

[8] 刘胜军.混合流水线多目标调度优化研究 [D].淄博：山东理工大学，2016.

作者简介：彭勇（1976-），男，汉族，湖北黄冈人，硕士，副教授，研究方向：网络安全，智能计算;郑慧君（1985-），男，汉族，湖北孝感人，硕士，讲师，研究方向：控制理论及计算机应用。