流动性风险、水平效应与敏感效应

李延军　张蒙　刘华堂

摘 要： 基于CAPM模型及三因子模型引入流动性水平效应与敏感效应，以敏感效应度量流动性风险，从流动性水平与风险角度出发，运用固定GLS面板回归研究了2002年1月至2017年12月中国A股市场流动性水平效应与敏感效应的具体表现以及产生的流动性溢价效应。研究表明：流动性水平效应、敏感效应与中国股市超额收益率显著正相关，二者的影响遵循流动性溢价理论;相比较而言，水平效应对我国股市的影响更大，但敏感效应的作用不容忽视，敏感效应呈現出规模递减与流动性递减趋势;牛熊市下都存在由水平效应与敏感效应引起的流动性溢价效应，但牛市中该现象更加显著。

关键词：流动性风险;敏感效应;水平效应;流动性溢价;股市行情

中图分类号：F830.91   文献标志码：A   文章编号：1674-7356（2019）-03-0027-08

流动性影响股票收益率的途径有两种：流动性水平与流动性风险。流动性水平指在较短的时间内完成交易的能力，即流动性因素自身;流动性风险指由于流动性水平的变化而产生的不确定性，即流动性水平因素与其他变量的协方差。Amihud和Mendelson（1986）使用买卖价差作为流动水平的测量指标，构建了流动性与收益率的关系[1];Jacoby 、Fowler与Gottesman（2000）推导出了调整后的CAPM模型[2];杨朝军与王林芝（2011）通过建立新的流动性指标进一步研究了流动性水平溢价效应[3]。上述研究均得出证券市场存在显著的由流动性水平引起的溢价现象的结论，但也有学者呈相反观点。Ben-Rephael，Kadan和Wohl（2015）发现在过去二十年里，美国股票流动性大幅上升，但流动性溢价效应的显著性下降，频繁的交易活动虽然促进流动性的上升，但由于预期收益对流动性的敏感度降低，因而流动性溢价效应并不显著[4]。通常流动性越好，资产预期收益越低，但也有学者得出了相反的结论。Eiesw Arapu与Reinganum（1993）实证研究了资产定价中流动性溢价的季节性行为，结果表明由于季节性因素很强，1月存在正流动性溢价现象[5]。

资产定价研究领域对于流动性的研究分为流动性水平与流动性风险两方面。同国外资产定价研究领域的思路相同，研究初期我国学者便开始关注流动性本身（即流动性水平）对资产预期收益的影响，近几十年来国内外学者不断拓展流动性水平指标以及资产定价模型，使得对于流动性水平的研究已经非常成熟，关于流动性风险对资产定价影响的研究正不断深入展开。Bangia，Diebold与Schuerman（1998）以价差的波动度量了流动性风险，并提出了流动性调整后的VAR模型[6];刘洋和刘善存（2008）将收益率和流动性结合构造出了新的流动性风险指标，使用修正的Fama-French三因子模型分析了流动性与超额收益率的关系[7];刘晓青与杨一文（2015）对流动性进行离散型小波变化分解后，使用了GARCH-VAR模型度量流动性风险[8];张楗炆（2015）在三因子模型基础上加入由GARCH模型表示的市场收益对市场总流动性的敏感性，结果表明：中国股市存在显著的市场风险溢价、敏感性风险溢价和波动性风险溢价[9];李延军和王丽颖（2015）从投资者风险偏好视角研究了流动性风险的具体构成与沪深两市流动性溢价效应[10]。

本文以水平效应和敏感效应分别度量流动性水平和流动性风险，在F-F三因子模型的基础上引入流动性风险因素（敏感效应），比较研究流动性溢价效应的两个渠道——流动性水平和流动性风险在我国A股市场的表现，着重探讨不同情境下流动性敏感效应对投资者预期收益率的影响，进而为投资者管理流动性风险提供参考。

一、研究设计

（一）模型构建

本文在Lawrence Kryzanowski（2006）关于流动性溢价效益两个渠道——水平效应和敏感效应分类和界定的基础上[11]，遵循在资本资产定价模型（CAPM）基础上逐步引入流动性水平效应和敏感效应的思路，模型构建过程如下：

1. CAPM模型

式（1）中，ri表示i的月收益率，rf表示无风险收益率，rm表示市场利率，系数表示个股收益率对市场组合收益率的敏感性，也称基本beta，用以度量个股或投资组合相对市场的波动性，常被用于评估系统性风险。因而本文将预期报酬因纳为解释变量，在CAPM模型的基础上，本文模型的初步形式为：

2. Fama-French三因子模型

Fama与French（1993）首次提出了包含市场组合因子、规模因子、账面市值比因子的模型，三因子模型在CAPM模型的基础上添加了SMB（规模因子）与HML（账面市值因子）[12]。规模与账面市值比是影响超额收益的因素，但两种因子对超额收益的影响程度不同。Fama与French（2015）发现在美国证券市场中账面市值因子HML是冗余因素，该因素对预期收益的影响较弱[13];Wang 与Xu （2004）将三因素模型应用到中国股票市场，研究发现，规模因子是影响预期收益的重要因素，但账面市值比因子的影响较弱[14];Hilliard 与Zhang（2015）也发现了较弱的账面市值效应[15]。因而本文仅将规模因素纳为解释变量，该因素由市值的对数ln（vi）表示，在式（2）的基础上加入规模因子后可得模型：

3. 引入流动性水平效应与敏感效应的资产定价模型

式（5）为改进后的Fama-French三因子模型，该模型在三因子模型的基础上添加了流动性因素（L），又称经流动性调整后的定价模型。流动性影响证券收益率的途径有两种：流动性水平与流动性风险，流动性水平指在较短的时间内完成交易的能力，即流动性因素自身;流动性风险指由于流动性水平的变化而产生的不确定性，即流动性水平因素与其他变量的协方差。在此基础上，Lawrence Kryzanowski（2006）首次提出了流动性的水平效应与敏感效应。水平效应指资产组的流动性水平与市场流动性水平的差值（即L - l ），若流动性指标使用Amihud非流动性值，差值越大则表明资产组的非流动性超过市场非流动性的程度越大，则该资产组需要较高的收益补偿。流动性的敏感效应是资产组流动性beta（β）与流动性值（L）之积和市场流动性beta（β）与流动性值（L ）之积的差额（即β L - β L ），差额越大表明该股越易受到市场流动性波动的影响，则该股需要较高的收益补偿。流动性的水平效应是资产的一种特性，敏感效应则是一种流动性风险因素。

因而，为更全面的研究中国股票市场中流动性对超额收益的影响，我们将流动性的水平效应与敏感效应两种因素纳为解释变量。多数研究表明市场流动性是影响超额收益的重要因素，因此，为更有效的解释超额收益，模型中使用了市场流动性（l ）调整后的超额收益，即R = E（ri） - rf - l 。此外，我们假设该模型在迭代经济体中运行，以上期各因素对本期超额收益的影响开展研究。因此，在式（4）的基础上加入流动性的水平效应与敏感效应，可得到加入时间与个体因素后的模型（6），其中i表示个体因素，t表示时间因素。

R = α0 + α1 β + α2  ln（vit-1） + γ0 （l - l ） +

γ1 （βl - βl）（6）

（二）变量选取与说明

1. 股票流动性

本文采用Amihud（2002）提出的非流动性指标度量我国股市的流动性，Amihud指标综合考虑了交易额与交易量，补充了价格法与交易量法的不足，计算公式如下：

ILLIQim =  （7）

上式中，ILLIQim表示m期i股票的非流动性比率，rimt与Voldimt表示i股在t月期间交易的收益率与交易额。Dim为股票i在m月的交易天数。非流动性指标越大，表明一定交易量的变动将引起股价更大程度的变动，则股票的流动性越差。本文收集了300只股票的日涨跌幅、日交易金额以及月交易天数，使用上述公式计算出每只股票的月流动性指标，即Amihud指标。

2. 其他变量说明

根据模型（7），本文选取基本β、公司规模（lnvi）、流动性水平效应（L - l ）、流动性敏感效应（β L - β L ）作为解释变量，选取经流动性调整后的超额收益（ R  = E（ri） - rf - l ）作为被解释变量，相关变量及说明如表1所示：

（三）数据与样本

无论规模还是交易额，A股市场都是中国股市的代表，因此本文选取沪深A股所有股票作为研究对象。研究区间为2002年1月至2017年12月，共包含192个月。样本的选择基于以下原因：一方面，2002—2017年包含了中国股市的多种市场行情状态，2007年至2014年间中国股市处于低迷期，而2015年中国股市呈高涨趋势，因而选择2002—2017年作为研究区间可以观测到不同市场行情下的中国股市。另一方面，2000年前中国股票交易制度还不够完善，民众对中国股市还没有建立起足够的信心，因而2000年前的时间段不能有效解釋中国股市的表现。此外，为保证研究结果的有效性，我们剔除了ST股、PT股、长期停盘、交易天数少于10天、以及数据缺失的股票，最终选取300只沪深A股作为研究样本。本文数据源于WIND、同花顺（iFinD）、锐思（RESSET）等金融数据库，数据的整理在EXCEL中完成，数据处理采用Matlab与Eviews软件。

二、实证结果分析

（一）描述性统计分析

本文将选取的300只样本股票按以下方式分组：首先按市值大小将300只股票平均分为5组，每组分得60只股票，然后分别将5组股票各按照流动性大小再分为5组，由此共得到25（5 × 5）个资产组，每个资产组具有不同的规模与流动性特征。因此，模型（7）中i的取值为1-25，表示25个资产组，t为2002.01—2017.12。表2描述了将300只股票交叉分组后，25个资产组的解释变量（基本beta β、规模因子lnvit-1、流动性值L和敏感性水平βl）时间序列平均值。结果表明，基于规模与流动性进行分组后，不同资产组之间呈现出明显的规模差异与流动性差异。具体表现为：公司规模（lnvi）越大，资产组流动性越好;资产组对市场波动的敏感度（βl）呈现出规模递减趋势，例如，处于低流动水平时，敏感性值随公司规模的增大从13.1655降低为1.7115，这表明比起大规模上市公司，小规模上市公司对股票市场的波动更加敏感;此外，敏感因素还表现出了流动性水平递减效应，例如，将规模固定为小规模时，敏感性值随流动性的增加从13.165 5降低为2.075 5，说明流动性水平低的股票对市场的波动更加敏感。美国股市中个股流动性对市场波动的敏感度也呈现出规模递减与流动性递减效应，Chordia，Roll和Subrahmanyam（2000）认为这是“投资者飞向流动性”的结果[16]。

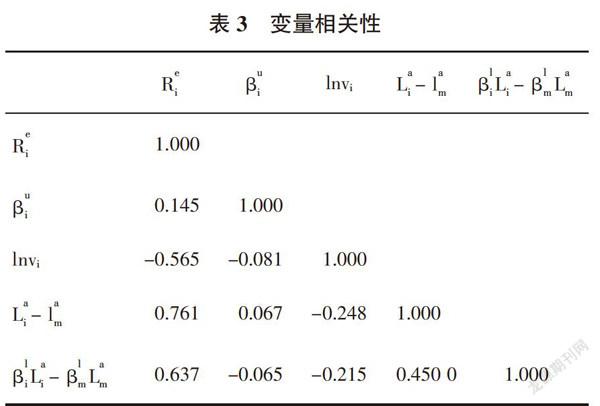
（二）变量相关性分析

表3描述了各解释变量的相关性，结果表明，各解释变量与被解释变量相关性较高，但各解释变量间相关性较小。R与β的相关系数为0.145，说明资产组与市场收益率的共变程度越大，该资产组所获得的超额收益越大;R与L  - l 的相关系数为0.761，说明资产组的非流动性水平与风险溢价呈正向关系，资产组的非流动性大于市场非流动性时，该资产组将获得收益补偿，即符合假设H1;Rβ L - β L 的相关性为0.637，表明流动性敏感效应与超额收益显著正相关，资产组受市场波动越敏感，则该资产组获得的收益补偿越大，符合假设H2。lnvi与R的相关系数为-0.565，可见规模效应与超额收益的相关性也较大，两者的负向关系同Fama French（1992）对美国股票市场的研究结果，即规模越大，其超额收益率越小。综上，初步可以判断出中国股市存在流动性水平效应与敏感效应，但仍需进一步进行面板研究。

（三）面板回归结果及分析

单位根检验结果表明，各变量的时间序列较为稳定;F检验结果表明，相对于混合回归模型，本文更适合使用固定效应模型，鉴于文章篇幅，单位根与F检验结果不再赘述。因而本文采用的计量方法为固定GLS面板回归，共检测了25个横截面（i=1-25）及192个时间序列（t=2002.01-2017.12），分别从规模因素、基本beta因素、流动性水平效应与敏感效应四个方面展开研究。

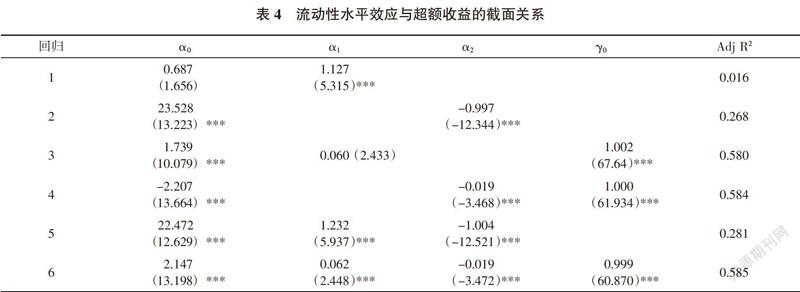
1. 流动性水平效应分析

表4中回归1、2分别表示基本beta、规模因子对超额收益的影响。回归1、2的结果显示：β与R正相关，即资产组合收益对市场收益的敏感性越强，则该组合的超额收益率越高;ln（vit-1）与R负相关，再次说明规模越大则该资产组获得的超额收益越小;回归1与2中变量的显著性水平较高，但模型的拟合优度较小，此外，回归1、2、3的常数项在0.05%的水平下显著不为0，说明仅考虑基本beta、规模因子两种因素不足以解释超额收益率，需要对影响因素作进一步研究。

表4中，回归3、4、6分别表示在基本beta、规模因素的基础上加入水平效应后对超额收益的影响。结果显示：首先，正γ0（水平效应的系数）同变量相关系数表得出的结果一致，表明当资产组非流动性大于市场非流动性时，该资产组获得较大的收益补偿;其次，水平效应具有的较高的显著性水平，可见流动性水平是影响超额收益的重要因素。最后，加入流动性水平效应后，回归6的拟合优度由0.281增长为0.585，常数项α0由22.472降低为2.147，显著性明显降低，可见增加流动性水平的模型增强了对超额收益的解释。

2. 流动性敏感效应分析

表5中，回归1、2如上，回归3、4、6分别表示在基本beta、规模因素的基础上加入了流动性敏感效应。结果显示：同相关系数表的结论一致，γ1（敏感效应的系数值）大于0再次说明资产组合流动性受市场波动越敏感，则该资产组获得的超额收益补偿越大。各回归模型中敏感效应的显著水平都较高，可见敏感效应也是影响超额收益的重要因素，说明我国A股市场存在显著的流动性风险溢价现象。在回归5的基础上增加敏感效应变量后，其拟合优度值大幅度上升，因此敏感效应提升了模型对超额收益的解释能力。此外，表5中其他变量也具有较高的显著水平，但均低于敏感效应因素，可见投资者进行组合投资时，不仅应当关注公司规模与β因素，更应关注该资产组合流动性对市场的敏感程度。

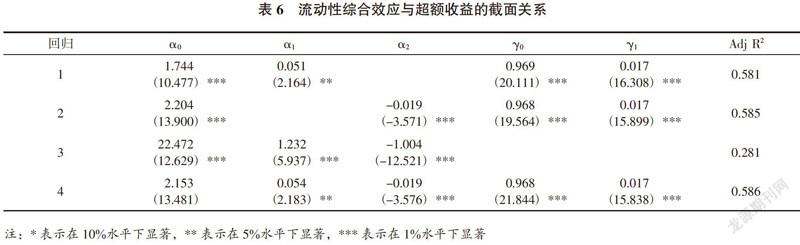
3. 流动性水平效应与敏感效应的综合分析

表6中，回归1、2、 4分别表示在基本beta、规模因素的基础上同时加入了流动性水平效应与敏感效应（综合效应）。结果显示：在回归3 的基础上同时加入水平效应与敏感效应后，拟合值大幅度上升，且增长幅度大于两种效应单独存在时的幅度，可见两种效应的综合作用不仅增加了对收益率的解释力度，且其解释能力大于两者单独存在时对超额收益的影响。对比水平效应与敏感效应可知：水平效应的系数小于敏感效应的系数，可见水平效应对超额收益率的影响大于敏感效应的影响。该结论不同于国外学者的研究结果，原因在于，较国外股市，中国A股市场較为稳定，因此资产组合对市场波动的敏感性较弱，因而资产组合获得的收益补偿主要源于自身流动性水平的匮乏，而非对市场波动的敏感性。

三、牛熊市行情下流动性水平效应与敏感效应分析

不同股市行情中流动性溢价效应会出现不同的特征差异，为保证上述结果的稳健性，我们将研究区间划分为牛熊市。对于牛熊市的划分并没有完全统一的评定标准，一般情况下，熊市的典型特征是：股指连续下跌、成交量下降、市场信心不足等，反之，随着股指上涨、股市交易逐渐活跃、市场参与者逐渐增多则可判定牛市即将来临。整体来看，中国股市在2007年10月达到6 124.04点之后，就逐渐进入了长达7年的熊市，这期间，股指连续下跌，成交量下降，市场信心严重不足，中间虽然有几次短暂的反弹行情，但由于动能不足，最终依旧在低位处徘徊。2008年至2011年间伴随着几轮短暂的牛熊市更迭，但由于金融危机的影响，市场情绪仍然处于一片恐慌之中，因此这期间的数据不具备代表性。鉴于此，本文选取2007年到2014年间熊市中的2011年11月至2014年6月作为分析熊市的数据区间。另一方面，2014年7月，随着沪港通、央行宽松政策对利好预期的刺激，上证股指开始上升，中国股市经历了长达11个月的牛市，具体来看，2014年7月23日起，上证综指日成交量超过了千亿，市场参与者大量增加，上证综指于2015年6月12日攀升到了5 178.19点，沪深两市的交易量也都突破了万亿，然而2015年下半年后股指迅速下降，股灾爆发。因此，本文选取2014年7月至2015年6月作为分析牛市的数据区间。不同行情下检验结果如表6所示。

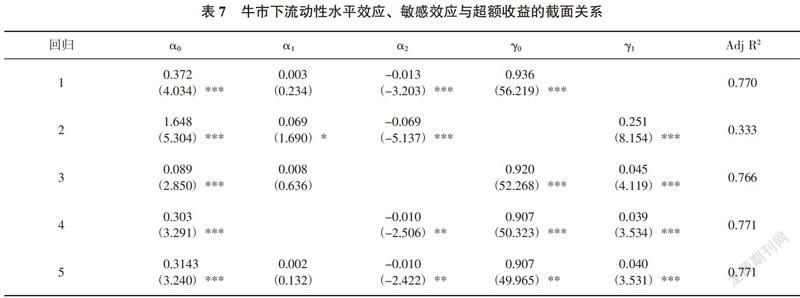
表7、表8的结果显示：在牛熊市行情下，β、ln（vit-1 ）、水平效应、流敏感效应对超额收益呈现不同程度的相关性：

第一，就基本beta而言，牛市中β与超额收益呈弱正相关，而熊市则呈显著负相关。这表明在熊市行情下，资产组合收益率与市场收益率共性越强，则该资产组的超额收益率越低，而该现象在牛市中则相反。可见，市场行情是影响基本beta与超额收益关系的重要因素。

第二，较熊市行情，牛市中规模因子ln（vit-1）对超额收益的影响更为显著，说明股市交易活跃的行情下，小规模公司股票获得较大超额收益的现象更为明显。

第三，牛、熊市行情下都存在由水平效应与敏感效应引起的流动性溢价，但相比熊市，牛市下水平效应与敏感效应的显著性水平更高。这说明，在股指上涨、成交量增加、股市交易活跃的行情下，流动性溢价水平效应更加突出，且受市场波动影响较大的资产组获得的收益补偿更大。但该结论有悖于其他学者的研究，一些学者认为牛市行情下，成交量增加、股市交易活跃，因而股票流动性较强，且股票间流动性差异较小，因而流动性不再视为风险因子，熊市则相反。

四、结论

主要研究结论如下：

一方面，中国A股市场中大规模公司股票流动性较好，该类股票不易受到股市波动的影响，因而获得的超额收益补偿较小;小规模公司股票流动性对股市的波动更加敏感，因此获得的超额收益补偿较大，可得出对于追求高收益的投资者在构建投资组合时更偏向于规模较小的公司股票，并且规模效应在牛市中更为显著;A股市场中资产组合呈现出显著正beta效应，表明资产组合收益率与市场收益共性越强，则该组合的超额收益率越高。但在熊市行情下，我们得到了显著的负beta效应，因此beta效应具有市场行情异质性。

另一方面，中国A股市场存在影响流动性溢价的水平效应与敏感效应，二者对超额收益的影响十分显著，且影响程度远大于规模因素与beta因素;资产组合的非流动性大于市场非流动性时，该资产组会获得较大的收益补偿;资产组合的流动性对市场波动越敏感，该资产组获得的超额收益补偿越大;同敏感效应相比，水平效应对超额收益的影响更大，但敏感效应的影响不容忽视，敏感效应呈现出规模递减与流动性递减趋势，即小规模上市公司与流动性水平低的公司股票对股市波动更加敏感;牛熊市下都存在由水平效应与敏感效应引起的流动性溢价效应，但牛市中更加显著，但该结论异于其他学者的研究，因而本文还需从其他流动性度量指标以及更精确划分牛熊市角度出发，进一步开展研究。

[参考文献]

[1]  Amihud Y，Mendelson H. Asset pricing and the bid-ask spread[J]. Journal of Financial Economics，2006，17（2）： 223-249.

[2]  Jacoby G，Fowler D J，Gottesman A A. The capital asset pricing model and the liquidity effect： A theoretical approach[J]. Journal of Financial Markets，2004，3（1）： 69-81.

[3]  杨朝军，王灵芝. 流动性水平、流动性风险对资产收益的影响——来自沪深股市的经验证据[J]. 系统管理学报，2011，20（4）： 456-461.

[4]  Ben-Rephael，A，Kadan，O. and Wohl，A. The Diminishing Liquidity Premium[J]. Journal of Financial and Quantitative Analysis，2015，50（1-2）： 197-229.

[5]  Eleswarapu V R，Reinganum M R. The seasonal behavior of the liquidity premium in asset pricing[J]. Journal of Financial Economics，1993，34（3）：373-386.

[6]  Bangia A，Diebold F X，Schuermann T，et al. Modeling Liquidity Risk，with Implications for Traditional Market Risk Measurement and Management[M]. Risk Management： The State of the Art. Springer US，2001： 3-13.

[7]  劉洋，刘善存. 上海股票市场系统流动性风险溢价研究[J]. 管理学报，2008，（2）： 263-268.

[8]  刘晓青，杨一文. 基于GARCH-VaR模型的股票流动性风险度量[J]. 计算机工程与应用，2015，（1）： 223-227.

[9]  张楗炆. 流动性风险与资产定价能力研究基于我国股市的实证研究[J]. 经济研究导刊，2015，（9）： 134-139

[10]  李延军，王丽颖. 股市流动性与资产定价——基于我国A股市场的实证研究[J]. 金融发展研究，2015，（7）： 9-15.

[11]  Zhongzhi（Lawrence） He，Lawrence Kryzanowski. The Cross Section of Expected Returns and Amortized Spreads[J]. Review of Pacific Basin Financial Markets & Policies，2006，9（04）：597-638.

[12]  Fama E F，French K R. Common Risk Factors in Returns on Stocks and Bonds[J]. Journal of Financial Economics，1993，33（1）： 3-56.

[13]  Fama E F，French K R. A five-factor asset pricing model[J]. Journal of Financial Economics，2015，116（1）： 1-22.

[14]  Wang Fenghua，Xu Yexiao. What Determines Chinese Stock Returns？[J]. Financial Analysts Journal，2006，60（6）： 65-77.

[15]  Hilliard J，Zhang H. Size and price-to-book effects： Evidence from the Chinese stock markets[J]. Pacific-Basin Finance Journal，2015， 32： 40-55.

[16]  Chordia T，Roll R，Subrahmanyam A. Commonality in liquidity[J]. Journal of Financial Economics，2000，56（1）： 3-28.

Liquidity Risk、Level Effect and Sensitive Effect

—— Empirical Test Based on Liquidity Premium

LI Yanjun， ZHANG Meng， LIU Huatang

（School of Economics and Management， Hebei University of Technology， Tianjin 300401， China）

Abstract： This paper introduces the level effect and incremental sensitive effect on the basis of the capital asset pricing model（CAPM） and the three-factor model， considers the sensitive effect as a proxy for liquidity risk， and uses a fixed GLS panel regression method to study the specific performance and influence of these two factors on liquidity premium from January 2002 to December 2017 of China′s A-share market. Studies show that level and sensitive effect have a significant positive effect on the stock′s excess return， which follows the liquidity premium theory. In comparison， the level effect has a greater impact on China′s stock market， but the sensitive effect shows a decreasing trend of size and liquidity， which cannot be ignored. The effect of liquidity premium caused by level and sensitive effects are presented in both the bullish and bear market， but this phenomenon is more pronounced in the bull market.

Key words： liquidity risk; sensitive effect; level effect; liquidity premium; market condition