航空发动机转子静、偶不平衡量控制方法研究
李鹏飞 王娟 赵洪丰









摘要:针对航空发动机转子静、偶不平衡量控制方法开展研究,基于坐标变换原理,以转子不同心度满足设计要求为约束条件,以转子静、偶不平衡量线性加权和最小为优化目标,提出了一种转子不同心度与不平衡量的计算方法,应用该方法对某型发动机的风扇转子进行了分析,表明该工艺方法能够明显改善转子不平衡量,达到控制转子静、偶不平衡量的目的。
关键词:转子;不平衡;不同心;线性加权;坐标变换;航空发动机
中图分类号:V231.96 文献标识码:A DOI:10.19452/j.issn1007-5453.2019.03.003
航空发动机转子在工作中高速旋转,转子的不平衡量对整机的振动响应有较大的影响,因此,转子装配在整机装配中占有重要地位。发动机的转子通常由多级盘通过止口定心、螺栓紧固的方式装配形成,目前国内发动机转子的装配方法主要有平面矢量合成法和堆叠优化装配法,平面矢量合成法的思路是测量部件的静不平衡量,装配时将部件的轻点(重点)进行平面矢量合成,以合成矢量最小为各盘相对角度,这种方法主要考虑部件单独不平衡量对组件的影响,忽略了止口跳动对部件惯性轴、旋转轴的影响,转子装配后,组件跳动、初始不平衡量均可能存在不合格的情况。堆叠优化装配法的思路是用堆叠优化转台分别对转子部件进行跳动测量,按照组件柱面同心度最小给出部件的安装角度,根据此安装角度进行转子装配。这种方法考虑了止口跳动对转子不平衡量的影响,但忽略了转子部件单独不平衡量,转子装配后,组件跳动合格,但初始不平衡量可能不合格。参考文献在未考虑转子跳动的情况下,给出了一种采用Powell法的转子不平衡量优化算法,参考文献在参考文献的基础上,给出了一种基于遗传算法的不平衡量优化方法。
本文介绍了一种基于坐标变换原理的转子不平衡量及不同心度计算的方法,可以实现任意盘间安装位置的转子组件不同心度和不平衡量的预测,并通过线性加权法实现转子静、偶不平衡量的控制和优化。
1转子不同心度、不平衡量计算原理
发动机转子组件由多个部件装配而成,各部件的同心度偏差通过一定的组合方式形成转子的同心度偏差,不平衡量可以看作转子质心相对旋转轴之间的位置关系,通过测量转子各部件连接面的偏差及质心位置,利用坐标变换,就可以计算得到不同组合方式下转子各部件质心位置相对组件旋转轴的空间坐标,从而可以计算出组件不平衡量的大小。通过此方法,可以获得任意安装位置下转子组件的不同心度和不平衡量,计算流程如图1所示。
2部件跳动及不平衡量测量
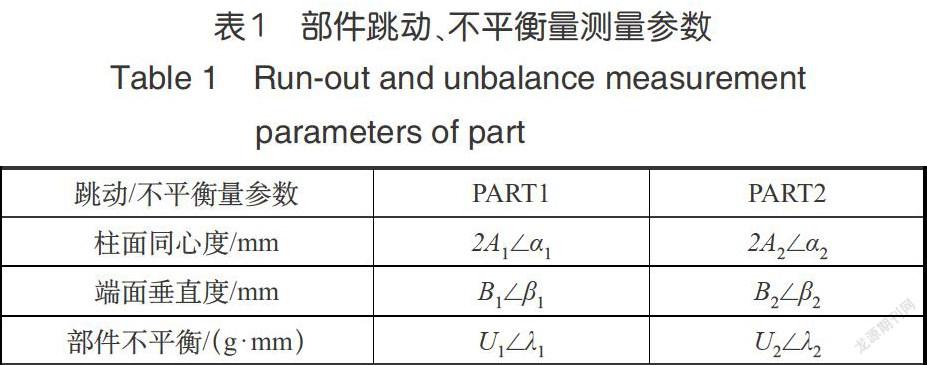
在转子装配前需要测量部件的跳动及不平衡量,跳动测量采用发动机转子堆叠优化转台,堆叠优化转台可以分离出被测量的形状公差和位置公差,不平衡量测量采用动(静)平衡机。航空发动机的转子通常设计为多级盘结构,本文介绍最基本的转子组件仅含两个部件的情况,对于转子组件含多于两个部件的情况,可等效为部件两两装配形成,各部件的跳动及不平衡量测量参数结果,见表1,结构参数见表2。
3坐标变换方法及优化过程
3.1坐标旋转
給定空间直角坐标系OXYZ,若使其绕OY轴旋转一个角度ε(ε为由坐标轴正方向向原点逆时针旋转角度),可获得一个新的坐标系O'X'Y'Z',在齐次坐标下,空间任意一点在新坐标系中的坐标X',Y',Z',与其在原坐标系中的坐标X,Y,Z之间的关系为:
即空间坐标系绕Y轴逆时针旋转ε的旋转矩阵为:
同理,坐标系只绕OX、OZ轴逆时针旋转ε,相应的坐标变换矩阵为:
依次绕各坐标轴旋转坐标系,可将坐标系旋转到任意姿态,相应的变换矩阵可由三个基本旋转矩阵相乘求得,即假设空间直角坐标系OXYZ,先绕OX轴旋转α,再绕OY轴旋转β,最后绕OZ轴旋转γ得到一个新的坐标系O'X'Y'Z',则变换矩阵表达为:
3.2坐标平移
给定空间直角坐标系OXYZ,将坐标原点依次沿OX轴正方向移动距离a,沿OY轴正方向移动距离b,沿OZ轴正方向移动距离c,可以得到一个新的坐标系O'X'Y'Z',在齐次坐标下,空间任意一点在新坐标系中的坐标X'Y'Z',与其在原坐标系中的坐标X,Y,Z之间的关系为:
T(a,b,c)为空间坐标系沿X轴、Y轴、Z轴正向分别平移a、b、c的平移矩阵。
3.3数学模型的建立
计算模型的建立基于以下假设条件:
(1)部件各连接面端面为理想平面,柱面为理想圆,即忽略止口跳动的形状公差,止口跳动仅表现为位置公差;
(2)部件为刚性装配,各部件连接面圆心重合。
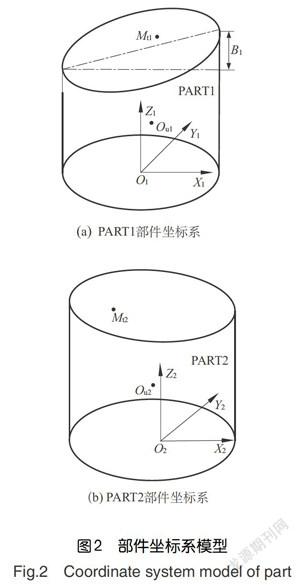
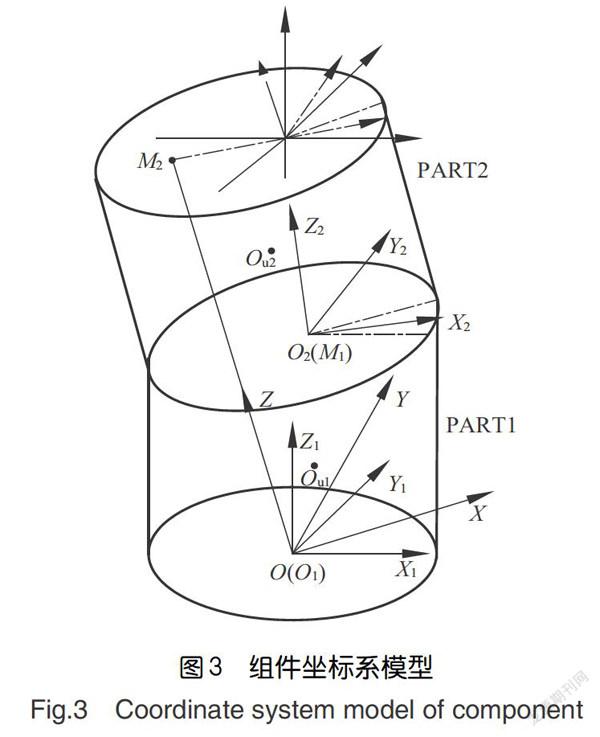
图2(a)、图2(b)分别为两部件测量坐标系下的质心位置和连接面圆心位置,O-XYZ、O-XYZ分别为部件PART1及PART2的部件测量坐标系,图3为组件示意图,其中PART1的部件坐标系O-XYZ为组件的装配坐标系,O-XYZ为旋转坐标系,旋转坐标系的Z轴为转子前后支点的截面圆心连线。本文建立的数学模型的部件跳动测量坐标系与部件不平衡量测量坐标系一致,若实际情况存在部件跳动测量坐标系与部件不平衡量测量坐标系不一致的情况,还需要将部件的质心坐标由不平衡量测量坐标系变换至部件跳动测量坐标系中,另外,该计算模型的部件不平衡仅表现为静不平衡,实际工程应用中,应根据实际单盘的宽径比选择机件进行动平衡或静平衡。
各部件、组件下连接面圆心与质心符号表示见表3。
3.4部件测量坐标系下质心坐标及连接面圆心坐标
根据部件不平衡量和质量,可以得到部件在不平衡量测量坐标系下的质心坐标为:
根据部件跳动测量结果,可以得到部件在部件跳动测量坐标系下各截面圆心坐标为:
采用列矢量表达,形式为:
3.5装配坐标系下质心坐标及连接面圆心坐标
以PART1为装配基准,PART2相对PART1零相位的装
配角度为angle12(后视逆时针为正方向)。实际上,航空发动机转子各部件均由n个螺栓连接形成组件,因此,angle 12的取值应为:
部件PART1质心在装配坐标系下的坐标为:
部件PART2装配到PART1上,部件PART2质心在装配坐标系下的坐标O为:
部件PART1后止口圆心在装配坐标系下的坐标为:
部件PART2后止口圆心在装配坐标系下的坐标为:
3.6旋转坐标系下质心坐标及连接面圆心坐标
将装配坐标系变换到旋转坐标系可通过先绕坐标轴旋转相应角度得到,其变换矩阵表达为:
式中:M(i,j)为矩阵M第i行、第j列的元素。
旋转坐标系下,各连接面柱面圆心坐标M及质心坐标O表示为:
3.7组件不平衡量叠加
一般情况下,转子的不平衡量由两类基本不平衡混合而成,即静不平衡与偶不平衡。通常用两个特定平面上的不平衡矢量来描述转子的动不平衡。有时也将它分离成静不平衡和偶不平衡来描述。本文采用转子的静不平衡和偶不平衡来描述转子的平衡状态。
如图4所示,在组件状态下,设部件PART 1及PART2质心截面上分别存在静不平衡量U、U,S为组件质心位置,可将不平衡量进行矢量合成,转换成一个静不平衡量U和一个偶不平衡量U。
对所有部件的不平衡量进行矢量相加,即可得到转子组件的静不平衡量大小:
令 ,则组件静不平衡量(平衡重点)相位:
对所有部件的不平衡量与部件相对转子组件质心距离矢量的不平衡量力矩进行矢量相加,即可得到转子组件的偶不平衡量大小:
3.8优化过程
通过计算可获得任意安装位置的理论静不平衡量和偶不平衡量,如果以组件的静不平衡量和偶不平衡量为优化目标,很难存在唯一解能同时使每个目标达到最优,但应具有各个目标之间相互妥协的一组最优解,针对该问题,通过线性加权和法将多目标优化问题转化为单目标优化问题,以某型发动机风扇转子为例,该风扇转子为三级盘结构,设计变量为各部件相对安装角度angle 12及angle23,目标函数表达为:
式中:W和W分别为函数的加权因子。可根据分目标函数的容限法求加权因子W和W的值,设分目标函数值的变化范围为:
则各项目标的容限为:
加权因子的选取写为:
这样,确定了分目标函数的上限值和下限值,即可确定加权因子,这种取法可以起到平衡各分目标函数数量级的作用。
约束条件为各盘止口或盘缘相对回转轴线的同心度≤0.03mm。
4算例
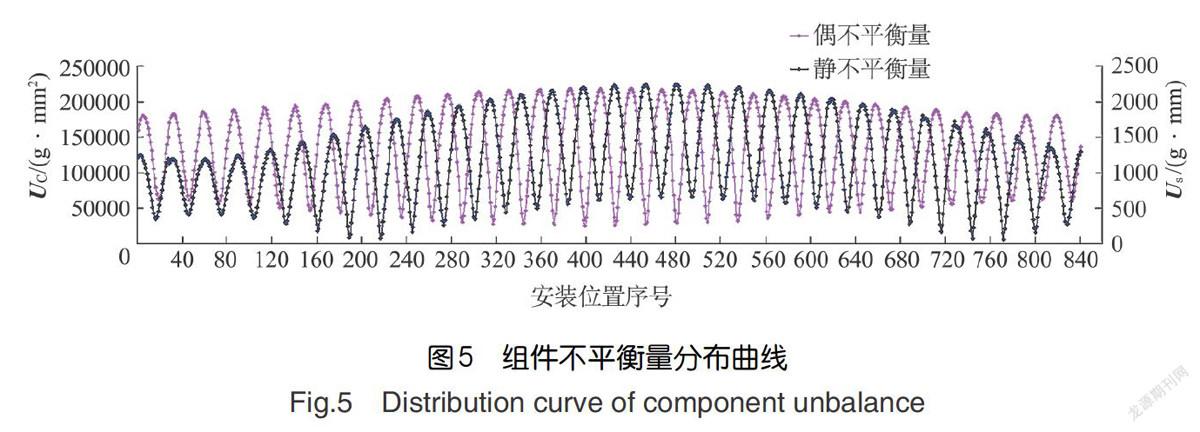
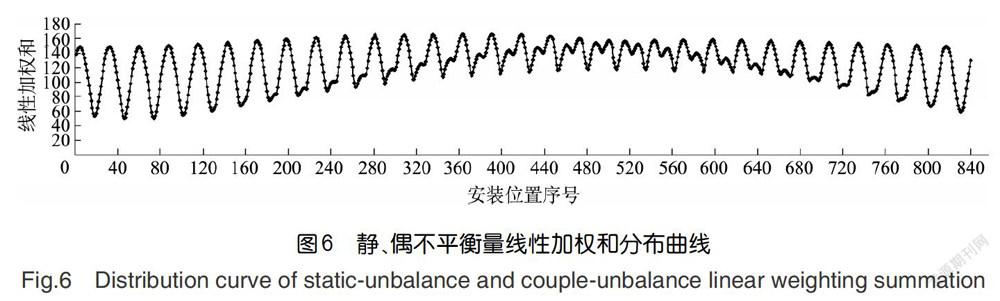
某型发动机的风扇转子中的一、二级盘通过28个螺栓连接,二、三级盘通过30个螺栓连接,则转子组件装配共有840个装配位置,根据单盘宽径比,确定一、三级盘进行静平衡,二级盘进行动平衡,每级盘的跳动、不平衡量的大小和方向取值见表4。使用MATLAB对以上算法进行了编程,计算得到转子组件840个装配位置的組件静不平衡量U和偶不平衡量U分布曲线如图5所示,组件静、偶不平衡量线性加权和分布曲线如图6所示。
以组件静、偶不平衡量线性加权和最小为最优解,确定一、二级盘安装角度angle12=218.57°,二、三级盘安装角度angle23=12°,优化位置与随机位置组件的同心度与不平衡量数据对比,见表5,可见该方法确定的装配位置在跳动满足图纸要求的前提下,相对随机位置能够明显改善转子的不平衡量。
5结论
通过分析,可以得出以下结论:
(1)通过测量转子部件的跳动及不平衡量,利用坐标变换原理,通过坐标变换可以估算出任意安装位置转子组件的不同心度与不平衡量。
(2)以转子组件不同心度为约束条件,并利用容限法确定转子静、偶不平衡量的加权因子,以转子静不平衡量、偶不平衡量线性加权和最小为优化目标,确定的装配位置可以实现组件不同心度满足设计要求的前提下,组件不平衡量最优。
(3)应用该工艺方法对某型发动机风扇转子进行了分析,结果表明该工艺方法能够明显改善转子不平衡量,达到控制转子静、偶不平衡量的目的。
本文介绍的工艺方法可以广泛应用于航空发动机、燃气轮机等的转子装配。
参考文献
[1]曹茂国.多级盘结构转子的工艺装配优化设计方法[J].航空发动机,1994(3):48-52.
Cao Maoguo.Optimization technique for multi-disk rotor assembly[J].Aeroengine,1994(3):48-52.(in Chinese)
[2]李立新.基于遗传算法的多级盘转子平衡方案优化设计[J].振动、测试与诊断,2008,28(2):139-142.
Li Lixin.Optimum design for balance in multi-disk rotor installation based on genetic algorithm[J].Journal of Vibration,Measurement&Diagnosis,2008,28(2):139-142.(in Chinese)
[3]刘君,吴法勇,王娟.航空发动机转子装配优化技术[J].航空发动机,2014,40(3):75-78.
Liu Jun,Wu Fayong,Wang Juan.Optimization technique of aeroengine rotor assembly[J].Aeroengine,2014,40(3):75-78.(in Chinese)
[4]哈托·施耐德.平衡技术理论与实践[M].北京:机械工业出版社,1981.
Hato Scneider.Balancing technology theory and practice[M].Beijing:Mechanical Industry Press,1981.(in Chinese)
[5]SAEARJP4163 Balancing machines:Tooling design criteria[S].2003.

