装备体系结构脆性及其评价方法

蒋卓 盛锴

摘要：为了表征多元环境下装备体系在遭受自身或外部干扰和破坏后的抵抗能力，根据装备体系结构网络化的特点，在对其组成系统进行集对分析的基础上，对装备体系结构的脆性进行评价分析。该方法首先讨论了装备体系结构脆性及其传递机理，然后通过引入信息熵的概念来定量地评估了装备体系结构的脆性，用以衡量在危机因素发生时装备体系结构发生崩溃的不确定程度。最后，以舰载机保障体系为例，证明该脆性评价方法对于装备体系的设计具有一定的意义。

关键词：装备体系;脆性;熵;集对分析

中图分类号：V271.4+92     文献标识码：A     DOI：10.19452/j.issn1007-5453.2019.03.007

装备体系是指由多个装备系统组成，为完成一定作战目标而构建的更高层次的系统。装备体系结构是对装备体系定性的描述，它的主要功能就是使子系统高效地综合在一起从而能够完成特定的使命。对装备体系结构中存在的多种危机因素进行分析，并评价这些危机因素发生时体系发生崩溃的不确定程度即是体系结构的脆性分析，它是评价装备体系结构是否健壮的一种手段。

目前，国内关于装备体系的研究，多集中在航空航天、国防和通信等行业，遇到的问题则往往需要在未经测试的多元环境下进行应急处理。面对这种情况，传统的装备体系结构评价方法难免有所局限。国外针对体系的研究，多是集中在电力系统、武器系统等领域，这些研究普遍认為体系崩溃是由各组成系统的脆性触发和传递引起的。因此，开展装备体系结构脆性研究，不仅可以为装备体系结构的分析与评价提供有力的支撑，也为装备体系的设计、构建和演化发展提供了有益参考。

通过分析装备体系结构的脆性及其传递机理，本文引入熵和集对分析法来计算装备体系结构的脆性，给装备体系的评价提供了一种量化评价手段。最后，应用舰载机保障体系结构的脆性评价实例来验证该方法。

1装备体系结构的脆性

装备体系结构是装备体系发挥能力的支撑，完整的装备体系结构主要包括：组成系统、组成系统间的交互、组成系统与环境的交互、结构的指导原则。本文对于装备体系的研究从结构入手，借鉴复杂网络研究中脆弱性的说法，引入“脆性”这一特性来表征体系抵抗破坏或干扰的能力。

在现有研究中，关于脆性的定义有很多的讨论，但都是从系统的角度考虑的，并没有给出装备体系结构脆性的定义。基于现有关于脆性的讨论以及装备体系结构的特性，本文认为，在不确定的环境中，若装备体系的组成系统或部分要素在危机因素（自身的疲劳或外界的干扰）的诱发下，其状态从有序转变成无序，并最终发生崩溃，而在与其他子系统交换信息和能量的过程中，出现无序的状态依次传递的连锁效应，并最终导致整个体系崩溃的特性，即为装备体系结构的脆性。

装备体系结构中首先发生崩溃的部分称为脆性源，因脆性传递而导致崩溃的部分称为脆性接收者，这一传递过程则称为脆性激发。考虑到装备体系结构的层次性以及脆性传递过程大多是横向和纵向共同作用的结果，本文将装备体系结构划分为体系结构级、组成系统级和危机因素级。由于体系的脆性激发过程是由各组成系统之间的交互导致，因此，在体系结构的脆性激发过程研究中，研究组成系统之间的关系尤为重要。本文引入集对分析法来分析脆性激发中组成系统的脆性传递过程。装备体系结构的脆性激发过程如图1所示。

2基于熵的装备体系结构脆性评价

2.1装备体系结构的网络描述

装备体系结构往往具有网络的特点，因此，本文将装备体系结构抽象成网络进行研究，组成系统表示为网络中的节点V，组成系统间的交互表示为网络中的边则装备体系结构可以表示为G=（V，E）。

2.2装备体系结构脆性熵

信息熵是描述离散系统从有序到无序状态的一个重要物理量，而装备体系的崩溃正是这样一个变化过程。若一个概率系统有n个危机因素都会导致系统发生崩溃，其中任意一个危机因素以一定的概率出现都会产生信息，这些信息就是危机因素导致系统发生崩溃的不确定性的度量。该系统所产生的总信息量也就是脆性熵，且有：

式中：F为第i个危机因素，P为第i个危机因素发生的概率，H为第i个危机因素发生产生的信息，H（F，…，F，…，F）就是n个危机因素产生的总信息量，也就是脆性熵。

2.2.1脆性熵的组成

脆性熵是衡量脆性激发不确定性的熵值，包括体系的各个组成系统发生崩溃可能性大小的熵值、系统之间发生脆性传递可能性大小的熵值以及体系从外界吸收信息和能量进行自我修复可能性大小的熵值，分别表示为脆性危机熵、脆性联系熵和负熵。由于装备体系中负熵发生的情况很难度量，因此，本文不给出负熵的计算，则装备体系结构脆性熵由脆性危机熵和脆性联系熵两部分组成，如图2所示。

根据集对分析法中对两两事物之间关系的分析，在脆性激发过程中，脆性源和脆性接收者之间存在三种脆性关系：同一性、对立性和差异性。

显而易见，体系结构的脆性熵也是一种信息熵，可以将其表示为：

式中：E为体系的脆性熵;E为体系的脆性危机熵;E为体系的脆性联系熵。

2.2.2脆性危机熵

体系的脆性危机熵是用来度量整个体系结构发生崩溃的可能性大小，它是体系的各个组成系统的脆性危机熵的加和，根据脆性熵函数的形式，体系结构的脆性危机熵可以表示为：

式中：E为组成该体系的第j个系统的脆性危机熵;P为该组成系统第i个危机因素发生的概率;m为体系的组成系统的个数;n为组成系统包含的危机因素的个数。

2.2.3组成系统的状态矢量

体系结构中组成系统的状态矢量可以更直观地反映系统间的脆性传递过程。状态矢量可以描述为：

式中：V为第j个组成系统的状态矢量，v為第j个组成系统第i个危机因素的激发情况，且：

2.2.4组成系统的脆性联系矩阵

体系结构由多个系统组成，各个组成系统的脆性激发状态可以用状态变量表示，考虑到体系结构的复杂性，引入脆性关联矩阵优化脆性联系熵的计算。

体系结构的脆性激发过程中，若组成系统V发生崩溃，则组成系统V与组成系统V发生脆性同一、脆性对立和脆性波动的概率可以用状态矢量表示，分别是、，且满足。

则可建立系统V到系统V的脆性同一矩阵A：

因为不考虑体系结构中组成系统崩溃对自身的脆性联系的影响，因此脆性同一概率。同理，也可以得到脆性对立矩阵B和脆性波动矩阵C。

考虑到组成系统之间的脆性关联应该是由脆性同一、对立和波动的共同体现。因此，装备体系结构中组成系统的脆性关联矩阵可表示为：

式中：L为m×m阶体系结构脆性联系矩阵;w，w，w为权系数，分别反映了三种脆性联系对脆性传递过程的影响程度，在工程应用时可由专家评判来给出具体权重系数。

2.2.5脆性联系熵

脆性联系熵是度量装备体系结构中脆性传递过程的不确定程度。整个体系结构脆性联系熵为：

式中：L为体系结构脆性联系矩阵，l为脆性联系矩阵中第j行k列的元素。

2.3体系结构脆性评价步骤

根据上述体系结构脆性熵的定义，本文提出的基于熵的体系结构脆性评价方法，其具体步骤如下：（1）根据体系的特性，构建体系结构脆性评价的危险因素集。首先将体系分割成几个系统进行评估，然后根据系统的特点给出脆性激发的危险因素。（2）根据体系的组成系统的危机因素确定组成系统状态矢量。因为初始状态体系结构的脆性不激发，所以状态矢量一般为零。（3）根据组成系统的状态矢量以及组成系统间脆性同一、对立、波动的关联，得到体系结构的脆性联系矩阵。（4）根据脆性联系矩阵和熵的计算公式，计算出体系结构的脆性熵。（5）分析脆性熵的计算结果，得出结论。

3案例分析

本文以舰载机保障体系为例来说明体系结构的脆性评价方法的应用。在航母作战体系或航母战斗群中，大多数作战使命都由舰载机来完成，因此，舰载机是航母战斗群发挥战斗力的重要部分。同时，给舰载机提供保障的众多保障系统具备体系的特征，属于保障体系，其保障舰载机的出动和回收从而形成航母战斗群的核心力量。由于在舰载机保障体系中存在着众多危机因素，这些危机因素的发生会导致组成系统发生故障或崩溃，从而导致舰载机的出动架次率不能达到预定目标，严重影响整个航母战斗群作战任务的执行情况。因此，对舰载机保障体系进行脆性分析并找到导致体系崩溃的薄弱环节，对于舰载机保障体系的设计和分析至关重要。

3.1构建危险因素集

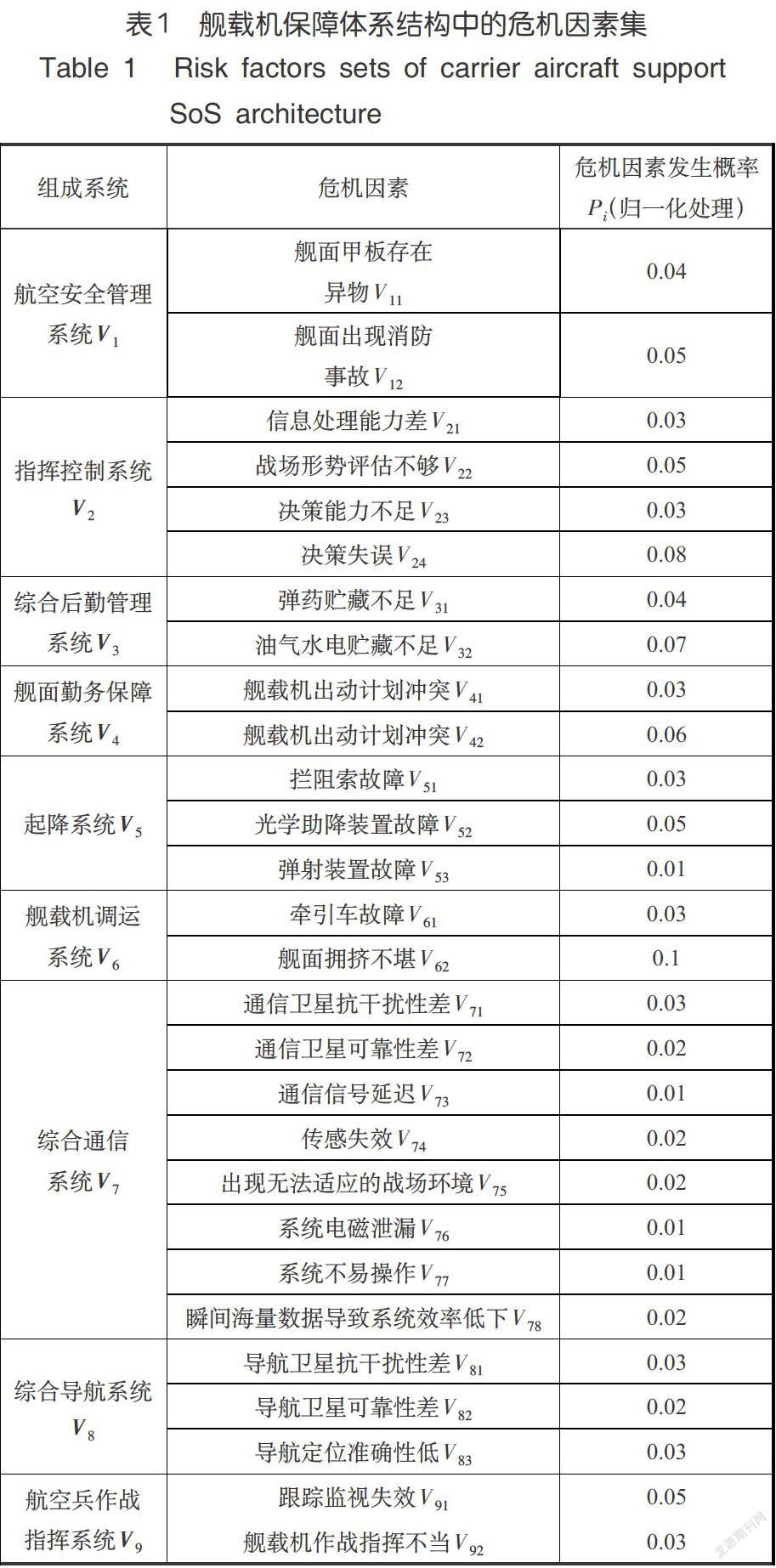
根据舰载机保障体系结构和地理条件、任务气候等特点，分析构成舰载机保障体系的9个组成系统的危机因素，从而可以建立脆性评价的危险因素集。舰载机保障体系结构中组成系统及导致各组成系统发生崩溃的危机因素见表1。

3.2计算脆性熵

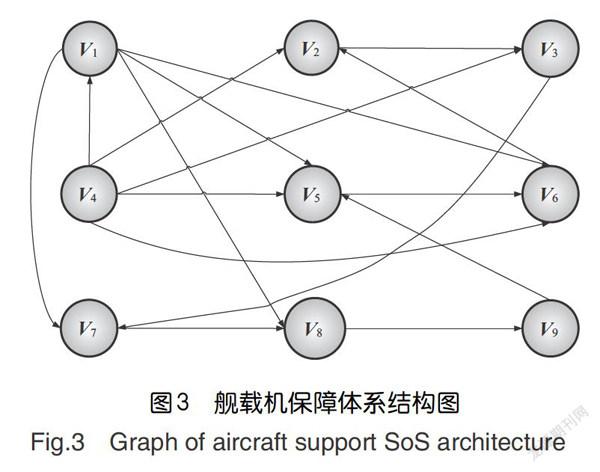
（1）给出舰载机保障体系结构图

可以将舰载机保障体系结构抽象成一个网络，每个组成系统就是一个节点。舰载机保障体系结构拓扑如图3所示。

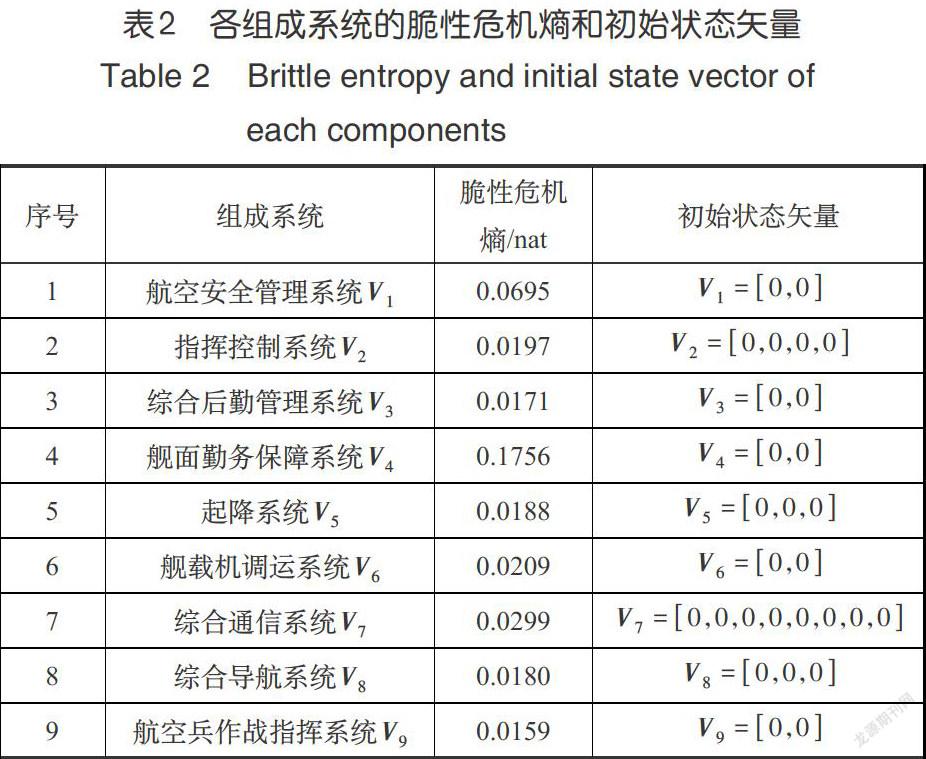
（2）计算舰载机保障体系的脆性危机熵

由式（3）可以得到舰载机保障体系的脆性危机熵为：

其中各组成系统的脆性危机熵见表2。

（3）给出各组成系统的初始状态矢量

由于初始状态时舰载机保障体系结构的脆性未激发，9个组成系统初始状态矢量见表2。

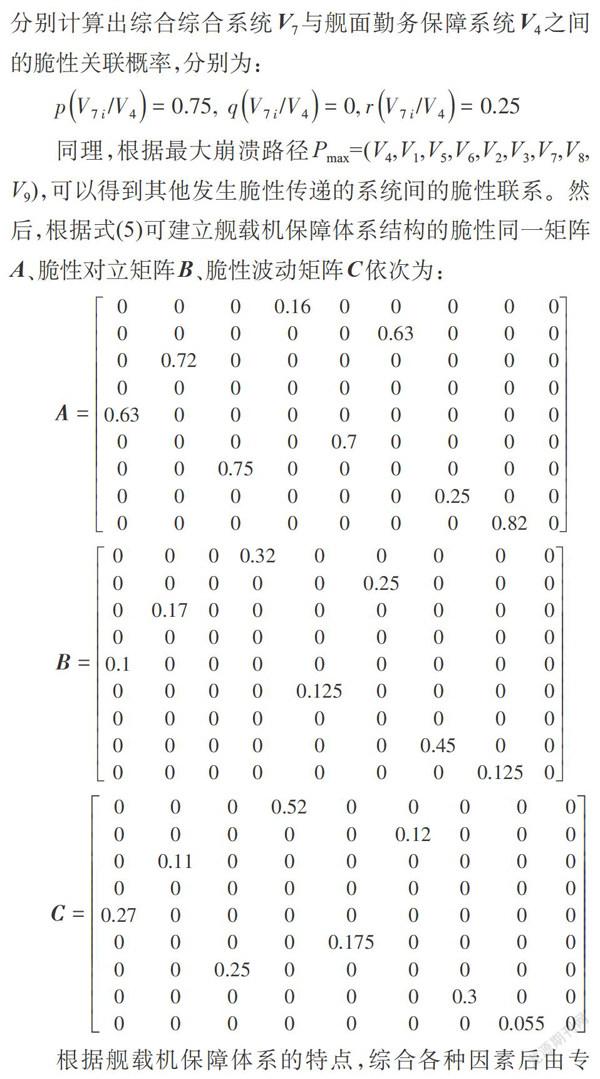
（4）计算体系结构的脆性联系矩阵

当舰面勤务保障系统V在危机因素发生导致崩溃时，综合通信系统V脆性同一的危机因素构成集合{V，V，V，V，V}，脆性波动的危机因素构成集合{V，V}，由此可以分别计算出综合综合系统V7与舰面勤务保障系统V之间的脆性关联概率，分别为：

同理，根据最大崩溃路径P=（V，V，V，V，V，V，V，V，V），可以得到其他发生脆性传递的系统间的脆性联系。然后，根据式（5）可建立舰载机保障体系结构的脆性同一矩阵A、脆性对立矩阵B、脆性波动矩阵C依次为：

根据舰载机保障体系的特点，综合各种因素后由专家评判赋予舰载机保障体系结构中脆性联系矩阵权系数w=0.7，w=0.1，w=0.2，由式（6）可得到脆性联系矩阵：

（5）计算体系结构的脆性联系熵

根据式（7）可得舰载机保障体系结构的脆性关联熵为：

（6）求出体系结构的脆性熵

舰载机保障体系结构脆性熵包括各个组成系统的脆性危机熵和组成系统之间的脆性联系熵，所以最终计算出舰载机保障体系结构的脆性熵为：

3.3结果分析

对于以上舰载机保障体系结构的脆性熵计算结果，可以从两个层面进行分析。

（1）组成系统层面

单独分析艦载机保障体系中各组成系统的脆性危机熵时，指挥控制系统的脆性危机熵大于其他8个组成系统的脆性危机熵，这说明当舰载机受到内部或者外部打击时，指挥控制系统极易发生崩溃，且崩溃后对整个舰载机保障体系的影响最大。因此，在设计构建舰载机保障体系时，需要重点关注指挥控制系统的脆性及其危机因素，降低其发生崩溃的可能。

（2）体系结构层面

综合分析舰载机保障体系的脆性危机熵和脆性联系熵，因为其脆性联系熵大于脆性危机熵，说明相比于组成系统自身崩溃导致的脆性激发，系统之间的脆性关联更容易导致舰载机保障体系的崩溃，因此，在分析和设计、构建舰载机保障体系结构时，需要着重降低各个组成系统之间的脆性关联，尤其强调降低关键组成系统于其他系统的脆性联系，这样能够更加有效地降低舰载机保障体系结构的脆性，从而提高最终体系的可靠性。

4结论

本文通过引入脆性的概念，结合熵理论和集对分析法，为装备体系结构的评价提供了新的方法。通过分析，可以得出以下结论：

（1）装备体系结构脆性的概念的提出，为装备体系的评估和分析提供了新的思路。

（2）通过集对分析理论，建立了体系中各组成系统之间的失效关联模型，对体系的失效过程分析提供了一定的借鉴作用。

（3）引入脆性熵这样一个体系结构评价的新指标，不仅能够定量分析体系各个组成系统的重要度，还为体系的保障与维护提供一定的决策。

为使该方法适用性更加广泛，对装备体系进行脆性评价时应该进一步考虑自恢复对体系结构的影响。

参考文献

[1]谭跃进，张小可，杨克巍.武器装备体系网络化描述与建模方法[J].系统管理学报，2012，21（06）：781-786.

Tan Yuejin，Zhang Xiaoke，Yang Kewei.Research on networked description and modeling methods of armament system-of-systems[J].Journal of Systems and Management，2012，21（06）：781-786.（in Chinese）

[2]潘星，蒋卓，杨艳京.基于弹性的体系组件重要度及恢复策[J].北京航空航天大学学报，2017，43（09）：1713-1720.

Pan Xing，Jiang Zhuo，Yang Yanjing.Resilience-based component importance and recovery strategy for system-of-systems[J].Journal of Beijing University of Aeronautics and Astronautics，2017，43（09）：1713-1720.（in Chinese）

[3]Liu Hu，Tian Yongliang，Gao Yuan，et al.System of systems oriented flight vehicle conceptual design：Perspectives and progresses[J].Chinese Journal of Aeronautics，2015，28（3）：617-635.

[4]游光荣，初军田，吕少卿，等.关于武器装备体系研究[J].军事运筹与系统工程，2010，24（04）：15-22.

You Guangrong，Chu Juntian，Lv Shaoqin，et al.Research on weapon and equipment system of system[J].Military Operations Research and Systems Engineering，2010，24（04）：15-22.（in Chinese）

[5]Delaurentis D，Robert C.A system of systems perspective for public policy decisions[J].Review of Policy Research，2004，21（6）：829-837.

[6]Anjel T.Modeling and simulation of systems of systems：a survey[J].Cybernetics and Information Technologies，2013，13（2）：3-36.

[7]孟超，张强，焦楷哲.基于元胞自动机的某装备供电系统脆性建模[J].科学技术与工程，2014，14（03）：159-165.

Meng Chao，Zhang Qiang，Jiao Kaizhe.Model construction of brittleness of power supply system based on cellular automata[J].Science Technology and Engineering，2014，14（03）：159-165.（in Chinese）

[8]Wang Yuzhe，Zhou Lin，Wang Yi，et al.Brittleness of air defense equipment support command system[J].Complex Systems and Complexity Science，2013，10（4）：41-48.

[9]Mosleh M，Ludlow P，Heydari B.Distributed resource management in systems of systems：an architecture perspective[J].Systems Engineering，2016，19（4）：362-374.

[10]Liu Jian，Zhang Genbao，Li Dongying，et al.Reliability analysis for multi-state manufacturing system based on brittleness theory[J].Computer Integrated Manufacturing Systems，2014，20（1）：155-164.

[11]张华一，张晶晶.基于脆性风险熵的电力系统连锁故障预测[J].电力系统及其自动化学报，2015，27（4）：39-43.

Zhang Huayi，Zhang Jingjing.Brittle risk entropy based model for forcasting power system cascading failures[J].Proceedings of the CSU-EPSA，2015，27（4）：39-43.（in Chinese）

[12]舒宇，譚跃进，李菊芳.武器装备体系结构描述方法研究[J].系统工程与电子技术，2008，30（9）：1704-1707.

Shu Yu，Tan Yuejin，Li Jufang.Study on an architecture description method of weapon equipment systems[J].Systems Engineering and Electronics，2008，30（9）：1704-1707.（in Chinese）

[13]Liu Chunfeng，Zhang Liang，Yang Aimin，et al.The evaluation model of international science and technology cooperation based on set pair analysis[J].Journal of Interdisciplinary Mathematics，2014，17（1）：95-108.

[14]Lv Haitao，Yin Chao，Cui Zongmin，et al.Risk assessment of security systems based on entropy theory and the Neyman Pearson criterion[J].Reliability Engineering and System Safety，2015，142（CSA）：68-77