带缺陷钢丝绳拉伸力-磁耦合数值模拟

高志刚 苏三庆 王威

摘 要：金属磁记忆作为一种新兴的钢丝绳无损检测技术，可对钢丝绳应力集中及缺陷部位进行定位，但对其应力状态及损伤程度的量化关系研究不足。为探究带缺陷钢丝绳拉伸状态下应力与金属磁记忆信号之间的联系规律，将缺陷诱发的钢丝绳损伤判别视为钢丝绳应力变化导致磁记忆信号改变的问题。基于磁机械效应及力磁耦合理论，考虑弹性阶段及塑性阶段磁特性参数（磁导率、矫顽力）随铁磁构件应力变化的不同规律，创新性地提出考虑磁导率和矫顽力影响的力-磁耦合修正模型。采用ANSYS有限元模拟软件，对带缺陷的1×7型单股钢丝绳进行静力场计算和环境磁场共同作用下的三维静磁场计算，利用力-磁耦合修正模型对两种物理场进行力-磁耦合。通过与试验结果进行对比分析，发现改进的模型可以较好地分析钢丝绳的力-磁耦合模拟问题，为以数值模拟为手段的钢丝绳拉伸应力与损伤量化关系研究方法奠定了基础。

关键词：带缺陷钢丝绳;有限单元法;数值模拟;金属磁记忆信号;力-磁耦合

中图分类号：TG 356.45;TD 115.284   文献标志码：A

DOI：10.13800/j.cnki.xakjdxxb.2019.0410   文章编号：1672-9315（2019）04-0626-08

Abstract：As a new nondestructive testing technology，metal magnetic memory testing can locate the stress concentration and defect location of wire rope，but the quantitative study of the relationship between stress state and damage degree is insufficient.To explore the relationship between the stress and metal magnetic memory signal of stretched wire rope with defects，the identification of wire rope damage induced by defects and broken wires is considered as the problem of magnetic memory signal change caused by stress change of wire rope.Based on the theory of magnetic mechanical effect and force magnetic coupling，the modified model of force magnetic coupling is proposed innovatively with the different rules in mind of magnetic characteristic parameters （permeability and coercivity） varying with the stress of ferromagnetic components in elastic and plastic stages.ANSYS finite element simulation software is used to calculate the stretched single strand of 1×7 wire rope with defects in the static loading field and the static magnetic field.Then the two physical fields on magneto mechanical coupling was analyzed directly.Compared with the results of test，it is found that the equivalent force on the surface of the wire rope increases gradually with the increase of the load，and the stress at the defect location increases obviously.Finally，this study further proves the modified model of force magnetic coupling proposed can well analyze the force magnetic coupling simulation of steel wire rope and lay a foundation for the research on quantitative relationship between stretched stress and damage of steel wire rope by means of numerical simulation.

Key words：wire rope with defects;finite element method;numerical simulation;metal magnetic memory;force magnetic coupling

0 引 言

鋼丝绳广泛应用于矿山、建筑、桥梁等工程领域，在长期高频工作中，存在磨损、断丝、强度值下降、锈蚀等缺陷，如果不能及时检测替换，钢丝绳一旦破断，会造成重大事故。目前金属磁记忆检测[1-4]作为一种新兴的钢丝绳无损检测技术，可对钢丝绳应力集中及缺陷部位进行定位，但对其应力状态及损伤程度的量化关系研究不足。目前，金属磁记忆检测试验研究[5-9]大多为定性研究磁性号与应力之间的关系，而目前试验停留在定性阶段的主要原因是外界环境对磁场影响因素多，试验数量积累不足，而ANSYS有限元模拟法是分析铁磁构件[10-11]漏磁场分布与损伤程度或其他物理特征之间定量关系的有效方法[12-14]。然而，在数值模拟分析中，磁导率和矫顽力会随铁磁构件应力变化而变化，同时试件表面漏磁信号也会由于磁导率和矫顽力变化而发生变化，当构件进入塑性阶段后矫顽力对磁信号影响大于磁导率，现有的力-磁耦合本构模型[15-17]能够很好的模拟弹性阶段磁导率和应力之间关系，但构件达到塑性阶段后铁磁构件磁畴发生不可逆重新取向，致使磁导率发生急剧变化，从而伴随产生较大的矫顽力，即矫顽力随磁导率降低而线性增加。随着塑性阶段应力的增加磁导率程线性递减，矫顽力成线性增加，这一现象目前的力-磁耦合本构模型不能真实体现，因此需要提出更符合实际受力状态的力-磁耦合本构模型。

针对钢丝绳的数值模拟研究，目前在模型上主要以构造简单的单丝为主，对整绳的数值模拟由于建模复杂，数值模拟研究甚少。尤其是应力状态下的考虑缺陷工况的整绳力-磁耦合模拟研究匮乏。文中基于磁机械效应及力-磁耦合理论，考虑弹性阶段及塑性阶段磁特性参数（磁导率、矫顽力）随铁磁构件应力变化的不同规律，提出考虑磁导率和矫顽力影响的力-磁耦合修正模型。利用该改进的模型进行有限元数值模拟，并与钢丝绳整绳拉伸试验[18-20]结果对比分析。为以数值模拟为手段的钢丝绳拉伸应力与损伤量化关系研究方法奠定基础。

1 修正的力-磁耦合本构

针对钢丝绳的数值模拟中本构关系存在的不足，本文对力-磁耦合本构关系进行了优化。在相关理论研究中[21-24]，磁导率和矫顽力作为铁磁性材料的两种主要宏观磁特性参数，会随着铁磁构件应力的增加而发生变化。而试件表面漏磁信号强度也会由于磁导率和矫顽力的变化而呈现一定的规律性。同时，当试件进入塑性阶段后，矫顽力对磁信号的影响大于磁导率。因此，此处提出了考虑磁导率和矫顽力影响的力-磁耦合修正模型。

在弹性阶段，矫顽力与应力成正比。然而相比磁导率，矫顽力的变化量可以忽略不计。因此，可以认为在弹性阶段矫顽力是恒定的。描述了磁导率与应力之间的关系，可以应用于弹性阶段。

在塑性阶段，铁磁材料的磁畴发生不可逆的重新取向，许多滑移带也随之产生，从而使磁导率急剧变化。而磁导率的变化将伴随产生较大的矫顽场。从上面分析可以得到，矫顽力随磁导率的降低而线性增加。磁导率随塑性阶段应力的增加呈线性递减。在模拟过程中，采用双线性等向硬化模型，可假设应力与应变为线性关系。因此，随着塑性阶段应力的增加，磁导率呈线性递减，矫顽力呈线性增加。此时磁机械耦合的修正模型可以用公式（1）和公式（2）表示。

2 钢丝绳力学特性模拟

2.1 钢丝绳几何模型的建立

建模用钢丝绳为1×7型单股钢丝绳[21]，其以一根钢丝为中心，外围再包捻一圈钢丝，同向捻制。取120 mm长的钢丝绳进行计算，其中每根钢丝直径为5 mm，外围钢丝每20 mm捻制90°.并在试件中间位置某一股上设置一个缺陷，缺陷宽度为1 mm，深度为0.1倍的钢丝直径。钢丝的弹性模量为2.04×105MPa，泊松比为0.3.按照由点到线，由线到面，最后由面拉伸成体的建模思路。

第一步，在三维笛卡尔坐标系下，建立7个圆的圆心关键点。第二步，分别以7个关键点为圆心，以2.5 mm为半径创建圆。第三步，将圆创建成圆面。最后，将7个圆面沿指定路径拉伸，相互捻绕而形成钢丝绳模型。但值得注意的是，此处指定路径是一条螺旋线，需要在柱面坐标系下建立。因此通过命令CSCY将三维笛卡尔坐标系转化为柱面坐标系，在柱面坐标系下建立螺旋拉伸线段L37和L38，两条线段沿Z方向延伸20 mm同时旋转90°，如图1所示。

将中间圆面沿Z方向拉伸40 mm，其余圆面沿先前确定好的螺旋路径L37和L38拉伸，即可得到一段40 mm长的钢丝绳模型，再利用COPY命令将模型复制三次，利用ADD命令将对应绳股两两相加，最终得到长度为120 mm的钢丝绳模型。在试件中间位置选择其中一股钢丝通过Create创建一个宽1 mm，深0.1 d的长方形，然后利用OVERLAP命令在钢丝绳表面形成一个矩形凹槽缺陷，如图2所示。

2.2 模型网格划分、接触对设置及加载

钢丝绳整体几何模型建立完成后，为了后期与三维静磁场中的单元对应，此处选用SOLID185单元[23]，在材料属性中分别设置弹性模型为2.04×105 MPa，泊松比为0.3，切向模量为2.04×104 MPa，名义屈服强度为1 640 MPa.单元类型和材料属性设定之后，对模型进行网格划分。采用SWEEP将钢丝绳进行扫掠划分，但由于带缺陷绳股沿长度方向截面有变化，无法直接使用SWEEP进行扫掠，因此采用FREE自由划分的方式对带缺陷绳股进行划分，网格尺寸统一为0.6 mm.并且为了使缺陷处的计算结果更加精确，对缺陷位置处的网格进行加密。网格划分之后的模型如图3（a）所示。

网格及节点耦合之后，需要进一步定义钢丝绳绳股之间的接触。而本文研究的钢丝绳为1×7型，其由1根繩芯和6根绳股组成，根据该型号钢丝绳结构特点，接触产生在股与芯及相邻的股与股之间，因此共需要建立12对接触对，其中两对接触对如图3（b）所示，在建立绳芯和绳股的接触时，绳芯为接触面绳股为目标面，在建立外层相邻绳股的接触时，每根绳股既做接触面又做目标面。一个接触对中的接触面和目标面必须有相同的实常数号，不同接触对有不同的实常数号。

在钢丝绳绳股之间的接触对创建完成之后，接触单元上实常数的确定对结果的敛散性及准确性十分重要，而实常数的确定与实际环境有很大关系。通过反复验证，这里法向接触刚度因子FKN取0.1，最大的渗透范围FTOLN取0.1，其余参数均取缺省值。

对边界条件和载荷进行简化，约束钢丝绳一端所有自由度，在另一端选取所有节点施加竖向位移载荷。另外，通过命令流设置非线性计算参数[22]，其中分析类型（ANTYPE）选择静态分析，将大变形或大应变选项（NLGEOM）打开，让程序根据模型中存在的非线性种类自动选择适合的牛顿-拉普森选项（NROPT，AUTO），并关闭自动激活自适应下降。其它参数默认。收敛准则（CNVTOL）采用力收敛准则，为降低收敛难度，TOLER值设为0.01.

2.3 钢丝绳力学结果

按照位移加载的方式，确定竖向位移加载分别为0.45和0.75 mm.通过上述分析方法，计算结果如图4所示。图4为不同竖向位移载荷下钢丝绳的横截面Von Mises等效应力云图。从图4可知，钢丝绳试件的等效应力随着竖向位移的不断增加而增加，同时试件的两个加载端应力较大，由圣维南原理解释：对于中间有效加载段，试件外表面的等效应力并不大，而且沿钢丝绳捻制的方向，等效应力基本维持不变。在绳股与绳股接触面位置，试件表面的等效应力较大，局部有应力集中产生。并且随着竖向位移的增加，应力集中的现象越显著。且绳芯受周围绳股的均匀压力，应力分布也较为均匀。

3 未加荷载时钢丝绳静磁场

将力学分析中钢丝绳几何模型直接导入静磁场分析当中，并在钢丝绳周围建立三维环形磁场，如图5所示。由于钢丝绳模型过于复杂，即使通过BTOL命令放松容限，也无法成功地对钢丝绳模型和空气层进行布尔运算。因此，只考虑其中带缺陷的一股钢丝，将其它股钢丝绳模型删除，同时提高了计算效率。此外，磁场模型同样选用三维静磁场单元SOLID97[24]，网格划分与力场分析保持一致，保证两个分析场中的单元对应。并在钢丝绳两端施加磁通量垂直边界条件，如图6所示。

未施加荷载状况下，钢丝绳表面的漏磁场强度只受环境磁场及试件自身的剩磁场影响。通过计算，得到初始阶段钢丝绳上带缺陷绳股的磁场强度云图，如图7所示。并沿试件z方向40到80 mm提取鋼丝绳表面法向磁场强度Hp（y），如图8所示。可以看出沿试件长度方向，钢丝绳带缺陷绳股表面的初始磁信号由负变为正，并在缺陷位置出现峰值，这与试验结果一致。

4 钢丝绳力-磁耦合

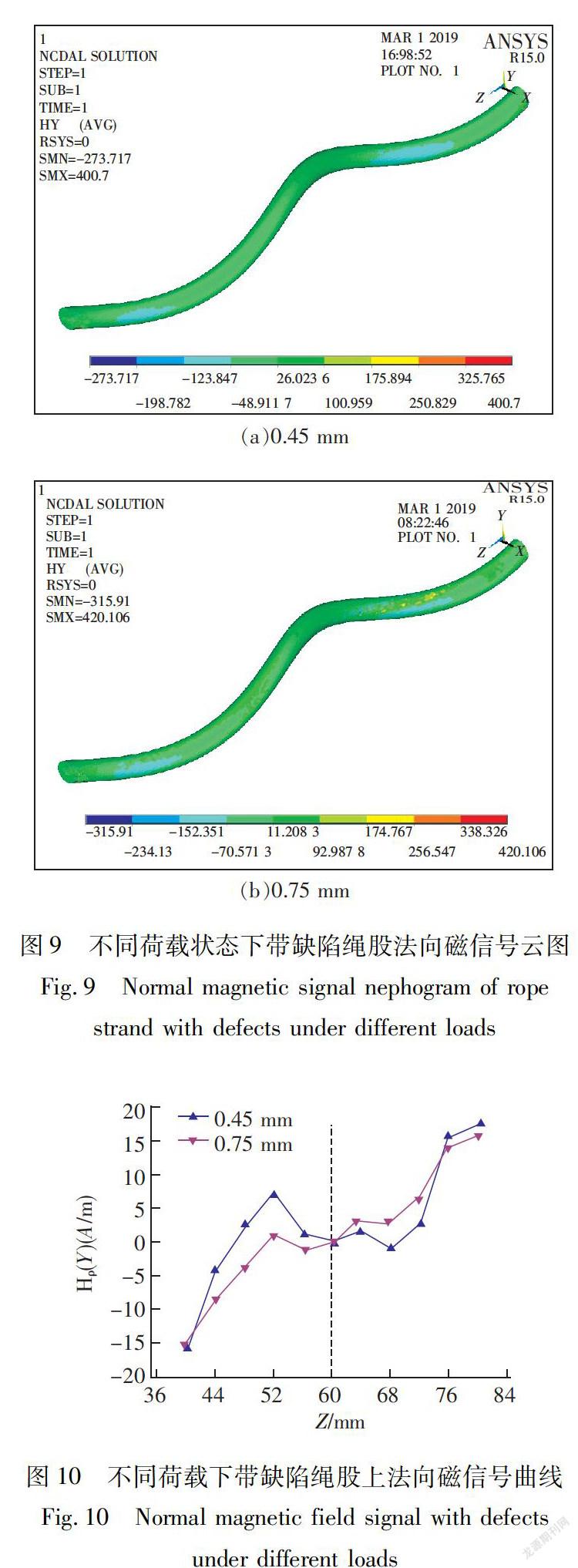
分别将竖向位移载荷0.45和0.75 mm的力学分析结果导出，并用上述钢丝绳修正后力-磁耦合模型公式计算钢丝绳带缺陷绳股的对应单元的磁导率和矫顽力。然后，将磁导率和矫顽力再次导入到对应单元中，进行静磁场计算。最后，得到不同加载状态下试件表面的磁场变化规律，如图9所示。

从图9可知，随着荷载的增加，试件表面的法向磁场强度有逐渐增加的趋势，这是应力不断增加，导致材料的宏观磁特性逐渐增加，进而导致磁场信号有所增强。沿钢丝绳捻制的方向提取试件表面的法向磁场信号，并与对应位置等效应力进行对比，如图10所示。从图10可知，沿试件的捻制方向，磁信号曲线有逆时针旋转的趋势，这是由于在竖向位移达到0.75 mm后，试件表面的等效应力超过材料的屈服应力，因此材料内部的晶格出现了大量的位错和滑移，从而导致宏观磁特性变化，即磁导率逐渐减小，矫顽力逐渐增大，从而导致磁信号出现转向零位置的趋势。

5 模拟结果与试验结果对比

取与数值模拟试验相同位置和长度区段的试验获取的磁记忆信号，如图11所示。缺陷位置为坐标中点，可以看出缺陷位置有明显的极值突变现象，由于环境磁场的影响，磁信号没有在零位置附近。未加载阶段初始状态模拟磁信号如图8所示。缺陷位置也出现明显的极值突变现象，且靠近零位置。梯度值作为初始环境磁场磁信号的有效特征量，可以反映缺陷或应力集中处相邻磁记忆信号的变化量，变化剧烈处存在极大值点。分别计算图11和图8中，缺陷处梯度值，试验梯度K1=2，数值模拟梯度K2=2.125.可以看出，初始环境下的磁信号，数值模拟与试验结果接近。

对比分析加载阶段的试验结果与数值模拟。首先计算数值模拟按位移加载对应的荷载等级，0.45和0.75 mm位移对应的荷载分别为50和100 kN.取与数值模拟试验相同位置和长度区段加载阶段的磁记忆信号，如图12所示。图12为数值模拟加载阶段的磁信号，从图12可以看出，试验和模拟与加载前的磁信号曲线相比较，加载后磁信号曲线中间位置处的波峰现象不再明显，磁记忆信号呈现单调的线性走势。这是由于在无外加应力状态下，试件表面的磁信号突变主要是由缺陷本身引起的漏磁场造成的。而加载后，由于整绳试件的受力状态变化，初始加载阶段缺陷位置的磁信号还是以缺陷本身引起的漏磁场变化为主，但是随着荷载增加，缺陷处等效应力减弱，其它检测点应力增加，磁信号将不断增大，故导致缺陷位置磁信号突变现象的消失。表1给出了加载阶段磁信号试验结果与数值模拟对比分析。

从表1可以看出，法向磁信号幅值变化试验结果和数值模拟有较好的相似度，随荷载增加相似度略有下降;整个测区的梯度值试验结果和数值模拟相似度较高，随着荷载的增加整个测区的梯度值试验结果与数值模拟更加接近，由此可知，试件整体因应力变化引起的磁感应强度变化力-磁耦合数值模精度较高;缺陷处的梯度值在初始状态数值模拟较为精确，加载后由于应力产生的磁感应强度变化对缺陷处的影响较大，在规律上能够看见峰值点消失，但梯度对比存在较大偏差，随着荷载的增加，应力引起的磁感应强度占主导地位，缺陷位置梯度数值模拟精度提高。

6 结 论

1）基于磁机械效应及力-磁耦合理论，考虑弹性阶段及塑性阶段磁特性参数（磁导率、矫顽力）随铁磁构件应力变化的不同规律，创新性地提出了考虑磁导率和矫顽力影响的力-磁耦合修正模型。

2）基于建立的力-磁耦合修正模型，发现带缺陷钢丝绳的早期损伤与金属磁记忆信号之间存在内在联系规律，法向磁记忆信号出现突变及过零点。随着荷载的增加，缺陷位置梯度数值模拟精度与试验接近。因此，改进模型可以较好地模拟分析钢丝的力-磁耦合问题。

3）ANSYS有限元数值模拟可以作为钢丝绳拉伸应力状态下损伤与应力量化关系研究的有效手段。

参考文献（References）：

[1] REN Shang kun，REN Xian zhi，DUAN Zhen xia，et al.Studies on influences of initial magnetization state on metal magnetic memory signal[J].NDT & E International，2019，103（3）：77-83.

[2]Mahdi Moonesan，Mehrdad Kashefi.Effect of sample initial magnetic field on the metal magnetic memory NDT result[J].Journal of Magnetism and Magnetic Materials，2018，460（16）：285-291.

[3]陶德馨，艾丽丝佳.基于弱磁探伤的钢丝绳无损检测技术[J].中国工程机械学报，2009，7（1）：96-99.

TAO De xin，AI Li si jia.Nondestructive testing technology for wire ropes based on weak magnetic flaw detection[J].Chinese Journal of Construction Machinery，2009，7（1）：96-99.

[4]王正道，姚 凯，沈 恺，等.金属磁记忆检测技术研究进展及若干讨论[J].实验力学，2012，27（2）：129-139.

WANG Zheng dao，YAO Kai，SHEN Kai，et al.Advances and evaluation of metal magnetic memory NDT technique[J].Journal of Experimental Mechanics，2012，27（2）：129-139.

[5]任吉林，林俊明，任文坚，等.金属磁记忆检测研究现状与发展前景[J].无损检测，2012，34（4）：3-11.

REN Ji lin，LIN Jun ming，REN Wen jian，et al.Metal magnetic memory testing technology development status and prospect[J].Nondestructive Testing，2012，34（4）：3-11.

[6]任吉林，邬冠花，宋 凯，等.金属磁记忆检测研究现状与发展前景[J].无损检测，2002，24（1）：29-31.

REN Ji lin，WU Guan hua，SONG Kai，et al.Study on the mechanism of metal magnetic memory testing[J].NDT，2002，24（1）：29-31.

[7]Doubov A A.A study of mental properties using the method of magnetic memory[J].Mental Science and Heat Treatment，1997，39（9-10）：401-402.

[8]Doubov A A.Screening of weld quality using the magnetic metal memory effect[J].Welding in the World，1998，41（10）：196-198.

[9]Doubov A A.Development of a metal magnetic memory method[J].Chemical and Petroleum Engineering，2012，47（11-12）：837-839.

[10]習小文.铁磁构件应力磁化及反转效应的数值模拟与试验研究[D].南昌：南昌航空大学，2015.

XI Xiao wen.Numerical simulation and experimental research of stress magnetism and magnetization reversal effect on ferromagnetic[D].Nanchang：Nanchang Hangkong University，2015.

[11]曾发荣，王 威，易术春，等.基于建筑钢结构拉伸试验磁记忆检测研究[J].钢结构，2015，30（1）：25-28.

ZENG Fa rong，WANG Wei，YI Shu chun，et al.Study of magnetic memory testing based on tensile test of building steel structure[J].Steel Construction，2015，30（1）：25-28.

[12]王 威，曾发荣，苏三庆，等.基于磁记忆的受弯钢梁力-磁效应试验[J].材料科学与工程学报，2016，34（1）：109-114.

WANG Wei，ZENG Fa rong，SU San qing，et al.Experimental research on magnetic mechanical effectiveness of bending steel beam based on metal magnetic memory[J].Materials Science & Engineering，2016，34（1）：109-114.

[13]欧阳春.应力集中及疲劳损伤磁记忆检测方法研究[D].南昌：南昌航空大学，2012.

OUYANG Chun.Stress concentration detection and fatigue damage assessment based on the metal magnetic memory technique[D].Nanchang：Nanchang Hangkong University，2012.

[14]曹印妮，张东来，徐殿国.三维漏磁场的钢丝绳局部损伤定量分析算法研究[J].电子学报，2007，35（6）：1170-1173.

CAO Yin ni，ZHANG Dong lai，XU Dian guo.Study on algorithms of wire rope localized flaw quantitative analysis based on three dimensional magnetic flux leakage[J].Acta Electronica Sinica，2007，35（6）：1170-1173.

[15]钱 康，尹爱军.基于力磁耦合效应的金属磁记忆仿真研究[J].重庆工商大学学报（自然科学版），2018，35（1）：1-6.

QIAN Kang，YIN Ai jun.Simulation research on metal magnetic memory based on force magnetic coupling effect[J].Journal of Chongqing Technology and Business University（Natural Science Edition），2018，35（1）：1-6.

[16]孙霁雯.力磁耦合原位拉伸/压缩测试单元设计分析与试验研究[D].长春：吉林大学，2017.

SUN Ji wen.Design analysis and experimental research on tensile/compression module of an in situ force magnetic coupled testing device[D].Changchun：Jilin University，2017.

[17]苏三庆，马小平，王 威，等.基于ANSYS有限元模拟的钢丝绳单丝拉伸力-磁耦合研究[J].西安建筑科技大学学报（自然科学版），2017，49（3）：309-316，331.

SU San qing，MA Xiao ping，WANG Wei，et al.Research on magneto mechanical coupling on tensile monofilament steel wire rope based on ANSYS finite element simulation[J].Journal of Xi’an University of Architecture & Technology（Natural Science Edition），2017，49（3）：309-316，331.

[18]周建庭，趙亚宇，何 沁，等.基于磁记忆的镀锌钢绞线腐蚀检测试验[J].长安大学学报（自然科学版），2019，39（1）：81-89.

ZHOU Jian ting，ZHAO Ya yu，HE Qin，et al.Experimental of corrosion detection of galvanized steel strands based on magnetic memory[J].Journal of Chang’an University（Natural Science Edition），2019，39（1）：81-89.

[19]魏英杰.基于微磁原理的钢丝绳无损检测方法研究[D].秦皇岛：燕山大学，2012.

WEI Ying jie.Method research on nondestructive testing for wire rope based on the micromagnetic theory[D].Qinhuangdao：Yanshan University，2012.

[20]陈厚桂.钢丝绳磁性无损检测技术的评估方法及标准研究[D].武汉：华中科技大学，2006.

CHEN Hou gui.Research on evaluation method and standard of wire rope magnetic testing technology[D].Wuhan：Huazhong University of Science & Technology，2006.

[21]张 瑾.1×7+IWS结构钢丝绳服役中应力应变的数值模拟[D].西安：西安理工大学，2009.

ZHANG Jin.Numerical simulation on the stress and strain of the 1×7+IWS steel wire rope in service[D].Xi’an：Xi’an University of Technology，2009.

[22]姚 凯，王正道，邓 博，等.金属磁记忆技术的数值研究[J].工程力学，2011，28（9）：218-222.

YAO Kai，WANG Zheng dao，DENG Bo，et al.Numerical study on metal magnetic memory technique[J].Engineering Mechanics，2011，28（9）：218-222.

[23]李龙军，王晓峰，杨宾锋，等.基于力磁耦合的金属磁记忆检测机理与仿真[J].空军工程大学学报（自然科学版），2012，13（3）：85-89.

LI Long jun，WANG Xiao feng，YANG Bin feng，et al.Based on the magnetic force coupling mechanism of metal magnetic memory testing and simulation[J].Journal of Air Force Engineering University （Natutal Science Edition），2012，13（3）：85-89.

[24]王社良，王 威，苏三庆，等.铁磁材料相对磁导率变化与应力关系的磁力学模型[J].西安科技大学学报，2005，25（3）：288-291.

WANG She liang，WANG Wei，SU San qing，et al.Magneto mechanical model on differential permeability and stress of ferromagnetic material[J].Journal of Xi’an University of Science and Technology，2005，25（3）：288-291.