简“形”相随，优化教学

黄远红

摘 要：“以形辅数”教学策略是有弹性的，它能最大限度地满足每一位学生的数学需要，最大限度地发挥每一位学生的智力、潜能。它既能为学习好、学得轻松的学生提供更多发展的机会，也特别关注学习上暂时有困难的学生。因此，在上一年的教学中，我已从一年级开始向学生渗透这种教学策略，让“形” 推动学生学“数”，成为“数”的助跑器，这也使我深深地体会到这种教学策略对教师的教学，对学生的学习都有极大的帮助。而在今年二年级的教学中，我更是适时、适当地渗透这种教学策略，引领学生对这种教学策略的再认识。

关键词：教学策略;以形辅数;新课程

“以形辅数”能有效防止学生进行“机械学习”，促进学生对数学知识的意义建构。我们应在数学教学中尽量发掘“数”与“形”的本质联系，借助“形”的慧眼，探索分析问题和解决问题的方法，为学生学习数学的发展思维而努力。在课题研究的推动下，我在本学期的教学中，对北师大版二年级下册的教材作了深入的研究，课堂中不断向学生渗透这种有效的学习策略。下面我引用自己教学中的三个例子试着说明和分析“以形辅数”教学策略的妙用。

1 动手画一画，画出题意

“以形辅数”在数学知识的教学中，不能轻视，尤其是经历了教师以其作为课题研究学生在这种教学策略的学习下，能通过“形的直观性和形象性理解数之间的关系。随着教学思考的日趋理性，我在备课中总是会先思考学生做题时会出现哪些错误的做法，针对这些错误的做法，再思考有什么“以形辅数”的教学方法来引导学生正确分析题意。

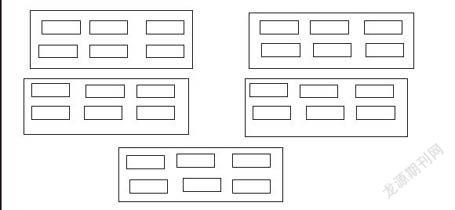
如同步练习第39页的第6题：一个大信封里有5个中等信封，每个中等信封里又有6个小信封，一共有多少个信封？这道题看似简单，但学生在审题时只在脑海中形成简单的影子”，就会出现以下错误做法：5+6=11（个），那如何让学生清晰明了地理解其中的包含关系及数量关系呢？其实，我们根据数学信息，直观、形象地画出“信封”（如下图）。这样就能明了地让学生分析题意，理解问题“一共有多少个信封？”并列出式子：5×6=30（个）。

经历上述画图过程后，学生对这道题的思路逐步清晰可见，学生在画图的活动中，能感悟策略、发展思维、体会方法和获得思想。可见，“以形辅数”的教学策略已成为小学生学习数学的一种需要。

2 动手连一连，连出意义

作为一线的教师，我对“以形辅数”的教学策略也有一个从迷茫到青晰，从无意识到自觉的认识过程。要实现有效教学，备好教学目标与教学重难点是最基本、最重要的前提。因此，我们备课时必须要深入地钻研教材，非常明确地把握好教学目标与重难点。只有把握好教学目标与重难点，才能在教学环节中使用好的教学策略。如课本第10页的“租船”一课时，我认为教学重点是理解“至少”，解决有关“至少”的实际问题，教学难点是使用正确的单位，理解商与余数的意义。在教学中，我除了借用“形”来让学生理解关键词“限乘”和“至少”，还用了连一连、圈一圈的简“形”突破难点，让学生正确使用相应的单位，更明了地理解商与余数的意义。其实，许多教学细节需要我们认真推敲，用心琢磨，把教学细节点亮。这一节课中，我仅仅使用了圈一圈、连一连的“小动作”，就对教学难点起到了画龙点晴的效果，也使其在课堂中起到锦上添花、以小见大的效应。

3 动手拨一拨，拨出算理

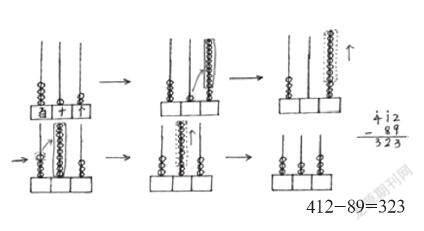
新课程提倡计算教学与解决问题紧密结合，有的教师因未能很好地理解新课程理念，在课堂上出现了算用颠倒现象。学生基本算理还没理解，教师就急着进行大量生活应用。还有的教师一味地重算法提炼，最终学生连基本的方法都不会，更不用说用熟练、灵活地进行计算，这样的教学，很难让学生掌握算理。课程标准明确提出：“计算教学时，应该通过解决实际问题进一步培养学生的数感，增进对运算意义的理解。”也就是说，学生既要懂得怎样算，更要懂得为什么要这样算。因此计算教学时，我们应该把教学重点放在算理的理解上，根据算理，掌握计算方法。在“三位数笔算的连续退位减法”的教学中，教材首先编排了口算、数线法、拨计数器三种方法，再介绍竖式计算。竖式计算的难点在于理解连续退位的算理，因此，我在教学中对口算与数线法两种方法是一带而过，重点放在用计数器理解连续退位的算理。课本出示的计数器图与现在所用的计数器实物很难让学生明白连续退位的算理，我就自制了一个计数器，用足够多的珠子演示了借1当十的过程。下面我就粗略的用草图表示一下计算的过程。

在演示的过程中，边引导学生观察，边组织语言说算理，如图例演示的算式：412减89， 个位上的2减9不够减，向十位借1当十，12减9等于3;十位上的1借走了1，还剩0，0减8不够减，再向百位借1当十，10减8等于2;百位上的4借走了1，还剩3，所以412减89等于323。这样，学生的思维跟着计数器走，加强了“说”的训练与“说”的指导，使学生学会说算理、说思路、说方法。几个例子后，学生就能脱离计数器，很容易地使用竖式计算做出正确的答案，并能随时随地说出每道题的算理。

“以形辅数”作为一种教学策略，无论“形”繁，“形”简，对学生分析问题，解决问题和有意义的学习具有很大的促进作用。但要充分发挥这种策略的價值，还需要教师在教学中不断探索，不断运用和体会、总结。在今后的教学中，通过“以形辅数”教学策略的应用，希望能够找到更多解决问题的良策，为学生分析问题、解决问题和思维训练提供更好的帮助。

参考文献：

[1] 雷玲.小学数学名师教学艺术[M]上海：华东师范大学出版社2012.

[2] 顾泠沅.数学思想方法发展概论[M] 北京：广播电视大学出版社，2004.