一种改进的变步长OMP图像重建算法

吴小龙 伍松

摘    要：为了快速、高精度的重建图像，解决滤波反投影（FBP）算法重建图像精度不高，正交匹配追踪（OMP）算法运行时间较长的问题，基于改变步长，提出一种步长变换正交匹配追踪（SCOMP）算法.当残差不小于阈值时，增大步长进行运算，当残差小于阈值时，恢复原步长进行运算.研究结果表明：SCOMP算法重建图像精度高于OMP算法，且运行时间快于FBP算法.SCOMP算法采用大步长快速添加原子，小步长有效去除原子的方法，使得重建图像的精度较高且运行时间也较短.

关键词：重建;反投影;正交匹配;步长变换

中图分类号：TN911.73          DOI：10.16375/j.cnki.cn45-1395/t.2019.04.011

0    引言

图像重建广泛出现在医学扫描，食品检测，加工装配等诸多领域，所以对于图像的重建在生产生活中非常重要.

滤波反投影（Filtered Back Projection，FBP）成像属于工业计算机断层成像（Industrial Computed Tomography，CT）技术.CT技术是一种由外到内的检测技术[1].FBP算法具有运算速度快的优点.国外关于滤波反投影的研究包括：Katsevich等[2]研究了不完全投影的滤波反投影重建算法.Pelt等[3]设计了一种关于数据的滤波器来减少投影产生的误差.国内西安交通大学，上海交通大学等也开始对该方面内容进行了研究.

正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法属于压缩感知（Compressed Sensing，CS），压缩感知理论首先由Candes等[4]提出.在国外，麻省理工学院、莱斯大学等一些知名大学已经成立了专门的课题组对此进行研究.国内很多研究单位的学者也已经开始对压缩感知进行研究，如清华大学、西安电子科技大学也都专门成立了课题组.

为快速、高精度的重建出图像，本文提出一种基于改变步长的步长变换正交匹配追踪（Step Change Orthogonal Matching Pursuit，SCOMP）算法，该算法运行时间较短，重建图像的精度较高.

1    压缩感知理论与OMP算法

1.1   压缩感知的基本原理

Donoho[5]提出并扩展了压缩传感理论，他用大量的实验证明了压缩传感在信号处理方面具有广阔的前景.根据压缩感知理论可得知，运用适当的重建算法能够从这些数据中高概率的恢复原始信号.压缩感知理论核心的思想是：将压缩与采样过程合并在一起完成，从而可以显著的减少采样点数，节省储存空间[6].

1.2   信号的稀疏表示

由文献[7]可知任意信号X可表示成下式：

[X=ΨΘ]                                       （1）

式中[Θ]是投影系数，其维数为N×1的列向量，Ψ为变换基.

1.3   測量矩阵

由文献[7]可知，测量信号[Y] 可表示成下式：

[Y=ФΘ=ФΨTX=ACSX]                                （2）

式中[Ф]是测量矩阵，[ACS]是传感矩阵.

1.4   优化重构

首先，若信号X[∈]RN在某一个变换基[Ψ]上是能够稀疏表示的，那么变换系数可以写作[Θ=ΨTX];然后，需要设计一个稳定的、与变换基[Ψ]不相关的测量矩阵[Ф]，对[Θ]进行映射，映射结果表示为[Y=ACS]（其中[ACS=ФΨT]）;最后，求解一个范数的优化问题[8]，从而解得原始信号X的精确解或者是近似解.重建过程如下式：

[minΘ0s.t.  ACSX=ФΨTX=Y]                             （3）

优化求得原信号X在变换基上的最稀疏表示[Θ]，然后作逆变换就可求得原始信号X.

1.5   OMP算法

正交匹配追踪算法是压缩感知中最为常用的一种算法[9].其核心思想是，在迭代过程中，要从传感矩阵[ACS]选出与观测信号Y相关度（内积）最大的那一列，然后从[ACS]中去掉该列并加入到扩充矩阵T中，接着求得残差r_n最小的一个估值aug_y，最后重复运行，达到迭代次数s为止.

OMP算法的基本核心步骤如下：

输入：观测信号Y，传感矩阵[ACS];

输出：原信号的稀疏逼近值theta;

初始化：残差r_n=Y（：，t0），储存集T为空集，Y的行数t0=0，迭代次数s=0;

Step1 找到传感矩阵[ACS]与残差r_n最相关的列[index_ACS]（s）=max_index;

Step2 更新索引集T=[T，[ACS]（：，[index_ACS] （s））];

Step3 使残差最小aug_y=pinv（T）* Y（：，t0），更新残差r_n=Y（：，t0）-T*aug_y;

Step4 直至迭代次数结束.

2    FBP算法

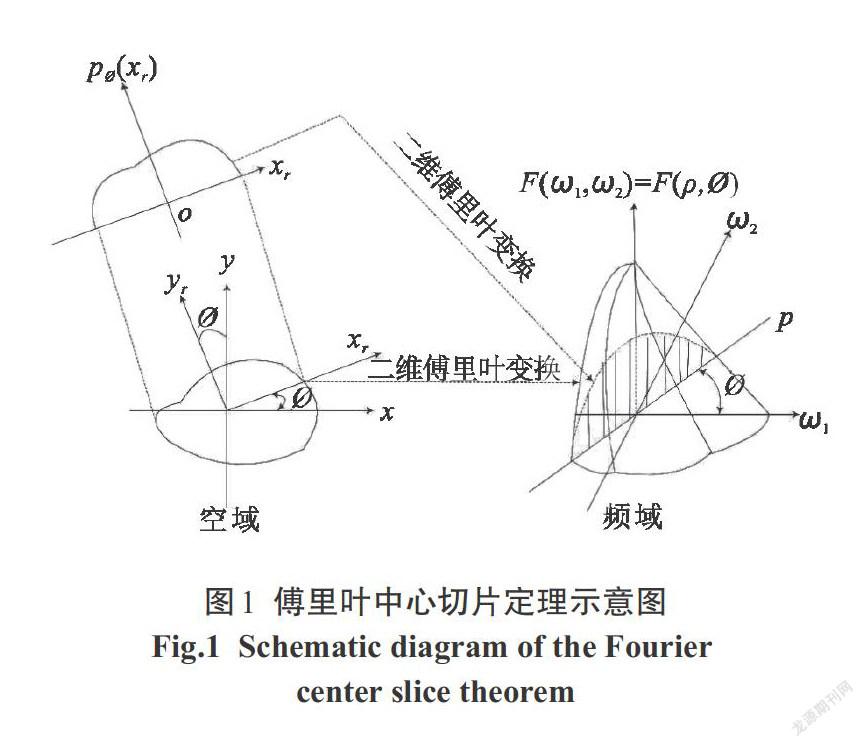
2.1   傅里叶中心切片定理

假设f（x，y）为待重构物体的密度函数，[pØ]（xr）为  f（x，y）在角度Ø=Ø0时的平行束投影.该定理的表达式为：

[F1[pØ（xr）]=F（ρ，Ø）|Ø-Ø0]       （4）

其中：F1[ ]是一维变换，F（ρ，Ø）是二维极坐标表示.

傅里叶中心切片定理[10-11]提供了频域上更简单的数学关系，即对物体的投影进行一维变换，如图1所示[12].

2.2   滤波反投影算法原理

滤波反投影重建算法是最常用的CT重建算法[13-14].滤波反投影重建公式如下：

[ftr， θ=fx， y=02πp（xr， Ø）*h（xr）dØ=02πg（xr， Ø）dØ]               （5）

式中，[ft（r，θ）]为[f（x，y）]沿直线的线积分，[h（xr）=F-11[ρ]]，[p（xr ， Ø）=F-11[p（ρ， Ø）]].

FBP算法基本核心步骤如下：

Step1 设计合适的滤波器[h];

Step2 把投影数据与滤波器进行卷积运算，得到投影数据[g（xr ， Øi）];

Step3 对于每一个角度[Øi]，把滤波后的投影[g（xr ， Øi）]反投影于满足[xr]，[rcos（θ-Øi）]的射线上的所有点[（r， θ）];

Step4 反投影数值进行累加，得到重建后的图像数据.

3    SCOMP算法

3.1   连续小波变换

函数f （t）连续小波变换表达式如下：

[ Wfa，b=ft ，  ψa，bt=1aRftψ*（t-ba）dt]                    （6）

小波变换的逆变换为：

[ft=1Cψ-∞∞-∞∞1a2Wfa，  bψ（t-ba）dadb]                       （7）

其中a与小波大小有关，b与位置有关，小波函数[ψ]（t）的傅里叶变换为：

[ψω=-∞∞ψ（t）e-jωtdt]                              （8）

当[Cψ=-∞∞ψ（ω）²ωdω<∞]时满足小波完全重构的条件，此时[ψ]（t）經过伸缩和平移得到波基函数：

[ψa，bt=1aψa，bt-ba ，  a，  b∈R， a≠0]                      （9）

3.2    DWT离散小波变换

在特征值提取时要采用连续的小波变换在每个可能的尺寸去计算小波系数，这样会产生大量的冗余数据，因此在实际的应用中连续小波必须加以离散化，这一离散化是针对尺度参数a和平移参数b的，而不是针对时间变量t的.

对a和b离散化，公式为：[a= aj0]，[b= aj0b0]，（j，k∈Z），a0为扩展步长，且a0≠1是固定值，对应的离散小波函数[ψj，kt]可写成：

[ψj，kt=a-j20ψt-kaj0b0aj0=a-j20ψ（a-j0t-kb0）]                    （10）

[Cj，k=-∞∞ψ*j，k（t）dt=f， ψj，k]                            （11）

式（11）为离散化小波变换的系数的求解公式.

3.3   SCOMP算法原理

OMP算法的步长是固定值1，这样就会导致计算的时间变长，从而影响效率.因此提出一种步长变换正交匹配追踪重建算法，当残差的长度大于阈值时，增大步长.即残差的长度若不小于阈值r2（norm（Res）≥r2），则步长会变大，以缩短运行时间，提高重建精度.

SCOMP算法基本核心步骤如下：

输入：M×N维测量矩阵Phi，观测信号y;

定义：前向步长α，后向步长β，阀值r1=eps*norm（y），r2=5×r1;

初始化：K=5α，eps=10-8，索引集T=[ ]，迭代次数n=0，残差Res=y，α=10，β=2;

Step1 计算残差Res和标准化测量矩阵Phinorm每一列的内积C=（Phinorm’*Res）;

Step2 将更新的α个原子放入索引集中T=（T;ind（1∶ α））并去除β个最小的原子T（ind（1∶ β））=[ ];

Step3 更新残差，若此时norm（Res）≥r2，则α变为20，β变为4，否则还是按照α=10，β=2运行;

Step4 如果T的长度大于N或者残差的长度小于r1，则结束运行，输出X，否则返回Step2.

对于前向步长与后向步长的取值，表1给出了实验数据：

可以看出，初始前后步长的差值与改变后前后步长的差值若是较小，会使运算时间变长且重构图像的精度变低;初始前后步长的差值与改变后前后步长的差值若是较大，此时运算时间较短但重构图像的精度会变低.

由此可得，要使运行时间较低且重建图像精度较高，则前后步长差值要适当，过长会导致重建过程中不能去除较差的原子使重建图像精度低，过短会使算法运行时间变长.且前后步长具体取值过大会导致迭代迅速结束，图像精度不高，过短会使算法运行时间变长.经试验，取初始前向步长α=10，后向步长   β=2，改变后的前向步长α=20，后向步长β=4，此时可以保证算法运行时间较短，重建图像精度较高.

对于给定值eps的取值，表2给出了实验数据.

eps的取值直接关系r1的取值，eps取值较小，r1较小，对迭代的精度要求高，则算法迭代的次数会比较多，可能会影响运算时间，eps取值较大，r1较大，则算法迭代的次数比较少，不能保证重构图像的精度.经试验，取eps为10-8，此时可以保证算法运行时间较短，图像重建精度较高.

对于r2的取值，表3给出了实验数据.

r2取值较大，则储存集保存的较大原子就多，但会增加运行时间，取值较小，储存集保存的较大原子就小.经试验，选取r2的值为5倍的r1，此时可以保证算法运行时间较短，图像重建精度较高.

综上所述，该算法中，对运行时间与重建精度影响较大的是前后步长的选取，因为前步长过大会直接影响运行时间，前步长过小则添加的原子数不够，遗失了较大的原子，影响重建精度;后步长过大会直接去除掉较大的原子，即增加运行时间，又影响精度，后步长过小则可能保留较小的原子，索引集的长度会变大，后面较大的原子可能不会被选入索引集中，影响重建精度.

4    实验结果

选取大小为256×256的Lena图像进行重建，软件为MatlabR2014b，3种算法重建的图像如图3—图5所示.其中OMP算法和SCOMP算法均用DWT离散小波进行信号稀疏，图像压缩比均为0.5，所用测量矩阵均为高斯随机矩阵，FBP算法测量角度为180°.各算法运算时间和峰值信噪比如表4所示.

图2为大小256×256的Lena原图.

图3为FBP算法重建图像，图像整体较为模糊，峰值信噪比较低.

图4为OMP算法重建图像，图像较为清晰，峰值信噪比较高，但从表中可以看出该算法运行时间比较长.

图5为SCOMP算法重建图像，取初始前步长α=10，后步长β=2，改变后的前步长α=20，后步长β=4，取定值eps=10-8，取阈值r2=5×r1，此时图像清晰度稍高于OMP算法重建图像的清晰度，且该算法的运行时间大大低于OMP算法的运行时间.

SCOMP算法采用大步長快速添加原子，小步长有效去除原子的方法，经过试验，可以使重建图像精度较高且运行时间较短，解决了FBP算法重建图像精度不高，OMP算法运行时间较长的问题.

5    结果分析

在对图像进行重建时，要平衡好运算时间与重建精度的关系，当通过某种方法使运算时间变短时要充分考虑到此改变对于精度的影响，并通过大量实验去验证.反之，当通过某种方法使精度提高时，要考虑该种方法是否会使运算变的冗长从而增加了运算的时间.在某一个因素改变时要对它改变的范围进行确定，充分了解该因素改变会对运算过程中哪些值产生影响，并思考如何去抑制不良的影响，也要考虑改变的值相互之间是否有影响.有时一个因素的改变会对结果产生较差的影响，此时可以对两个或者多个因素进行改变.此外，还要注意对主要因素的控制，因为该因素会对结果产生最大的影响，要将该因素的值控制在一个合理的范围，再对其他因素进行改变寻找最合适的取值.SCOMP算法较好的平衡了运算时间与重建精度的关系.

6    结束语

未来可从以下几方面进行研究：一是将步长变换正交匹配追踪算法与滤波反投影算法相结合进行图像重建;二是提高步长变换正交匹配追踪算法重建图像的精度;三是可以通过除残差长度外的其他因素来判断是否要进行步长改变;四是可以进行三维的重建.

参考文献

[1]    张朝宗，郭志平，张朋，等.工业CT技术和原理[M].北京：科学出版社，2009.

[2]    KATSEVICH A，RAMM A. Filtered back projection method for inversion of incomplete tomographic data[J].Applied Mathematics Letters，1992，5：77-80.

[3]    PELT D M，BATENBURG K J. Improving filtered back-projection reconstruction by data-dependent filtering[J].IEEE Transactions on Image Processing，2014，23（11）：4750-4762.

[4]    CANDES E，TAO T.Decoding by linear programming[J].IEEE Transactions on Information Theory，2005，51（12）：4203-4215.

[5]    DONOHO D.Compressed sensing[J].IEEE Transations on Information Theory，2006，52（4）：1289-1306.

[6]    陶佳偉，李春贵.基于压缩感知的肝脏CT/PET医学图像融合研究[J].广西科技大学学报，2015，26（3）：32-33.

[7]    杜宝.基于压缩感知的平面近场声全息理论与实验研究[D].昆明：昆明理工大学，2017.

[8]    汪霜霜，李春贵.一种lp正则化改进的车辆轨迹学习算法[J].广西科技大学学报，2019，30（2）：58-59.

[9]    SHEN Y，LI S. Sparse signals recovery from noisy measurements by orthogonal matching pursuit[J].Inverse Problems & Imaging，2015，9（1）：231-238.

[10]  RONALD N BRACEWELL. The fourier transform and its applications[M].西安：西安交通大学出版社，2005.

[11]  REN N G. Fourier slice photography[J].ACM Transaction on Graphics，2005，24（3）：735-744.

[12]  庄天戈.CT理论与算法[M].上海：上海交通大学出版社，1992.

[13]  范慧赟.CT图像滤波反投影重建算法的研究[D].西安：西北工业大学，2007.

[14]  余晓锷，龚剑，马建华.CT原理与技术[M].北京：科学出版社，2013.

An improved OMP image reconstruction algorithm based on

changing step size

WU Xiaolong1，2， WU Song*1，2

（1.School of Mechanical and Traffic Engineering， Guangxi University of Science and Technology， Liuzhou 545006， China; 2.Guangxi Key Laboratory of Automotive Components and Vehicle Technology（Guangxi

University of Science and Technology）， Liuzhou 545006， China）

Abstract： A step change orthogonal matching pursuit（SCOMP） algorithm is proposed to reconstruct  image with high speed and precision as the resolution of the filtered back projection（FBP） algorithm is not high and the orthogonal matching pursuit（OMP） algorithm has a long running time. When the       residual is not less than the threshold， the step size is increased. When the residual is less than the threshold， the original step is restored. The results show that the accuracy of SCOMP reconstruction