六参数粘弹性阻尼耗能减震系统非平稳地震响应分析的精细积分法
李创第 昌明静 柏大炼 王博文














摘 要:针对六参数粘弹性耗能减震系统,结合虚拟激励法,给出了非平稳地震响应分析的精细分析法.对于设置的支撑六参数粘弹性阻尼耗能系统的运动方程,首先,采用高效的虚拟激励法,将非平稳随机地震激励化为确定性荷载;然后,利用扩阶法,得到系统的状态方程;最后,给出了响应的精细积分解析解.并通过算例验证本文方法的精确性与实用性,为该方法推广应用于复杂大型结构的耗能减震工程提供新途径.
关键词:六参数粘弹性;精细积分法;虚拟激励法;耗能减震系統;非平稳地震响应
中图分类号:TU311.3 DOI:10.16375/j.cnki.cn45-1395/t.2019.04.003
0 引言
粘弹性阻尼装置控制结构振动是一种有效且广泛使用的被动控制方法,其模型主要有Maxwell模型、Kelvin模型、六参数模型等[1-3].其中,六参数模型计算参数便于实验数据拟合,具有通用性和工程实用性的特点,是一种实用的粘弹性阻尼器减震模型[4-6].为此,对该模型的耗能减震系统响应进行深入分析,具有重要的理论价值和实际意义.
在工程中,应用较多的是Priestley[7]提出的受演变随机激励非平稳随机响应分析.针对此响应分析,传统分析方法有CQC计算格式[8]和SRSS近似格式[9].但因这两种方法计算公式复杂,计算过程繁琐且成本巨大,计算效率难以在工程上广泛应用.林家浩等[10]提出的虚拟激励法,将随机激励化为确定性荷载,简化计算过程,节省了计算时间且结果依然相同,改善了传统方法的限制.虚拟激励法的提出解决了很多工程中重要而困难的问题,如大跨桥梁结构、风工程、车辆工程以及国防工程等领域,在国际上有较高的影响力[11].
在计算时程积分时,一般用Newmark,Wilson-θ等方法求解,但是这两种方法都存在耗时较长,精度有限等问题.钟万勰[12]提出的精细积分法,在积分步长不受结构自振特性制约的情况下,总能算出计算机精度范围内的结构响应.该方法目前已被广泛地应用于热传导、结构动力响应、结构优化设计、偏微分方程的求解等众多领域[13-14];精细积分方法与虚拟激励法结合,已经成功解决了无阻尼结构的非平稳随机地震响应分析[15-16],但至今尚未应用于粘弹性阻尼耗能减震结构的非平稳响应分析和阻尼系统抗震动力可靠度分析.
对于耗能减震系统的运动方程,本文利用虚拟激励法,将非平稳随机地震激励化为确定性荷载,利用扩阶法得出系统状态方程,并算出了响应的精细积分解析解.最终得出一套关于非平稳地震激励下,六参数阻尼耗能减震系统简明直观的精细算法.
1 阻尼器本构关系及系统运动方程
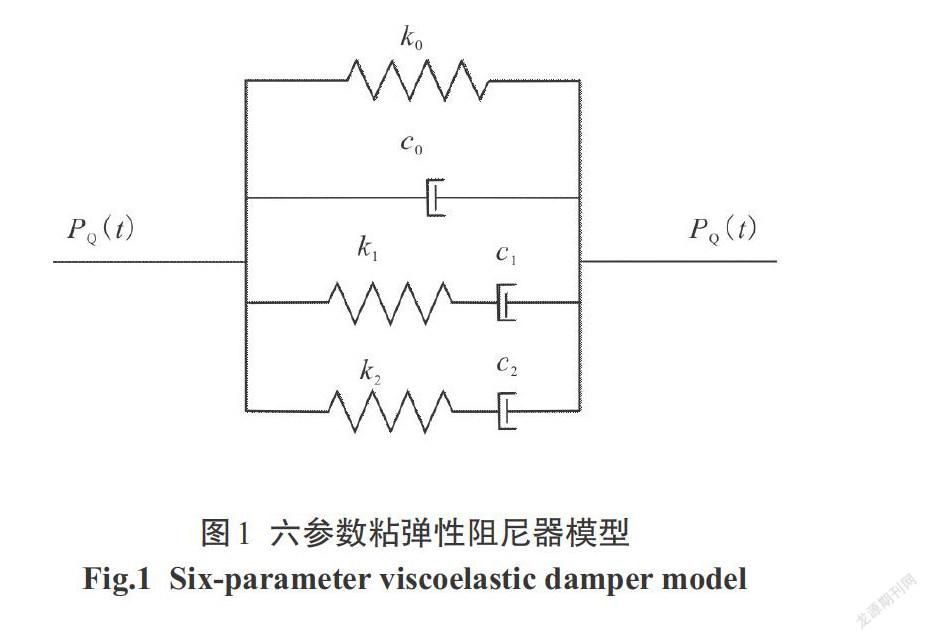
六参数粘弹性阻尼器模型如图1所示,该粘弹性阻尼器本构关系表达式为[4]:
[PQ(t)=k0xQ+c0xQ+P1(t) +P2(t) ] (1)
[P1+μ1P1=k1xQ] (2)
[P2+μ2P2=k2xQ] (3)
式中,[k0]为阻尼器的平衡刚度;[Pi(i=1,2)]表示六参数粘弹性阻尼器中两支Maxwell阻尼单元的单元阻尼力;[μi=ki/ci(i=1, 2)],[xQ]为阻尼器位移.
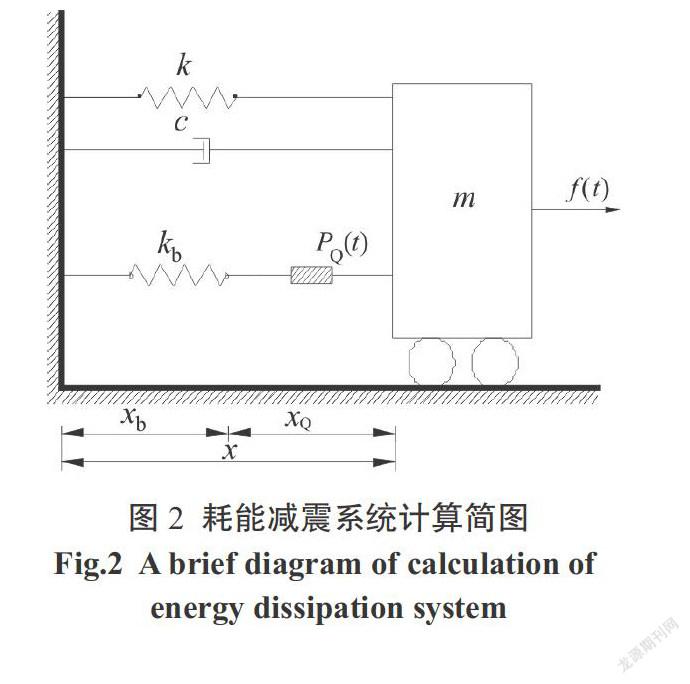
工程实际中,一般把支撑和阻尼器串联,计算简图如图2所示.[PQ]、[Pb]和[P]分别表示阻尼器受力、支撑受力和阻尼系统受力,[xb]和[x]分别为支撑和结构的位移,关系式为:
[P=PQ=Pb=kxb] (4)
[xb+xQ=x] (5)
结构在地震作用[f(t)]下的及运动方程为:
[mx+cx+kx+P=f(t)] (6)
2 六参数粘弹性阻尼减震系统响应分析
2.1 非平穩地震响应的虚拟激励法
实际地震中,地震发生的随机振动过程,一般视为非平稳随机过程,非平稳随机过程不是各态历经的,其各种统计信息随时间变化而变化.地震动过程通常包含两个非平稳过程,一种是强度非平稳,另一种是频率非平稳,为考虑这两种情况的共同影响,通常采用Priestley[7]建议的演变功率谱:
[xg(t)=-∞+∞a(ω,t)eiωtdα(ω)=a(ω,t)xf(t)] (7)
其中,[a(ω,t)]是满足[a(ω,t)=a*(-ω,t)]的确定性非均匀调制函数,*表示共轭,[xg]地震动地面加速度,[xf(t)]为零均值平稳随机过程,[i=-1].[α(ω)]满足下列过程:
[xf(t)=+∞-∞eiωtdα(ω)] (8)
[Edα*(ω1)dα(ω2)=δ(ω1-ω2)Sxf(ω1)dω1dω2] (9)
[Sxf](ω)为[xf]的功率谱密度函数.常用的有Kanai-Tajimi激励谱、Clough-Penizien谱、胡聿贤谱[10]等.
根据林家浩的虚拟激励法理论,如果构造非平稳虚拟地震激励为:
[xg(ω, t)=Sxf(ω)a(ω,t)eiωt] (10)
设在[xf(ω, t)]产生的响应表示为[v(ω, t)],那么响应的自谱密度即可表示为:
[Svv(ω, t)=v*(ω, t)v(ω, t)=I*(ω, t)I(ω, t)Sxf(ω)] (11)
式中,[I(ω, t)=0th(t-τ)a(ω, τ)eiωτdτ].
把非平稳虚拟地震激励(10) 代入振动方程(6)中得:
[mx+cx+kx+P=-mSxf(ω)a(ω, t)eiωt] (12)
2.2 六参数粘弹性阻尼减震的精细积分法
对于上面建立的非平稳虚拟激励的动力学模型,引入响应变量:
[v(t)=xxxQP1P2T] (13)
由式(12)结合恒等式[x=x]和式(1)—式(5),写入状态方程为:
[Bv(t)+Av(t)=F] (14)
其中,
[B=cmc000m000000c00000-c11000-c201] [, A=k0k0110-m000-kb0k0+kb11000μ100000μ2],
[F=-mSxf(ω)a(ω, t)eiωt, 0, 0, 0, 0T]
式(14)可改寫为:
[v=Hv+r] (15)
式中,
[H=-B-1A , r=B-1F] (16)
当步长足够小,即[t∈(tk, tk+1)],假定激励荷载变化是线性的,有:
[r=r0+r1(t-t0)] (17)
式中,[r0]与[r1]是时不变向量,则方程(15)的解为:
[v(tk+1)=T(τ)[v(tk)+H-1(r0+H-1r1)]-H-1(r0+H-1r1+r1τ)] (18)
式中,[τ=tk+1-tk]为积分步长.上式中出现的矩阵[T(τ)]的计算,首先将积分步长[τ]内部细分为[m=2N]等分,即:
[Δt=τ/m=2-Nτ] (19)
一般取[N=20],于是[Δt≈10-6τ],[Δt]一般远小于结构的自振周期.
[T(τ)=(eHΔt)m≈(I+HΔt+(HΔt)2/2!+(HΔt)3/3!+(HΔt)4/4!)m=(I+Ta0)m] (20)
令:
[I+Tai=(I+Ta,i-1)2=(I+2Ta,i-1+Ta,i-1Ta,i-1) ;i=1,2,…,N] (21)
得:
[Tai=2Ta,i-1+Ta,i-1Ta,i-1] (22)
那么,
[I+TaN=(I+Ta,N-1)2=(I+Ta,N-2)4=…=(I+Ta0)m=T(τ)] (23)
计算得到[Ta1 , Ta2 , …, TaN],进而得到[Τ(τ)],即可由式(18)得到各响应的解析解.
以上[T(τ)]的推导过程均为精确推导,可以看出只有一处近似,即式(20)的计算过程中忽略了[Δt5]及更高阶的项,其数量级已经超过[10-30O(τ5)],远超过使用计算机的精度范围.该方法过程简明易于理解且计算较精确.
综上步骤,六参数粘弹性耗能减震系统的位移[x(ω, t)]、速度[x(ω, t)]和阻尼器位移[xQ(ω, t)]即:
[x(ω, t)=v(1)] (24)
[x(ω, t)=v(2)] (25)
[xQ(ω, t)=v(3)] ; (26)
支撐位移[xb(ω, t)]:
[xb(ω, t)=x(ω, t)-xQ(ω, t)] (27)
[P(ω, t)=kbxb(ω, t)] (28)
阻尼力[P(ω, t)]可由式(28)得到,也可根据式(1)得到.
[P(ω, t)=kbxb(ω, t)] (29)
阻尼力速度[P(ω, t)]可根据对应的阻尼力求导,也可由式(29)得到.
阻尼器速度和支撑速度可根据对应的位移求导得到.响应的方差由式(18)得:
[σ2v(t)=-∞+∞Svv(ω)dω] (30)
3 算例
某单自由度带支撑的六参数粘弹性阻尼耗能减震系统,结构质量[m=38 600 kg],结构刚度 [k=146.01×105 N/m],阻尼比[s0]=0.04;阻尼器的平衡刚度[k0=0.36×105 N/m],阻尼参数[c0=0.37×105 N⋅s/m],两个Maxwell分支单元的刚度[k1=42.08×105 N/m],[k2=6.87×105 N/m],阻尼 [c1=0.83×105 N⋅s/m]、[c2=2.15×105 N⋅s/m];支撑刚度[kb=rbk];平稳地震动[xf(t)]谱密度函数采用
[Sxf(ω)=ω4g+4ξ2gω2gω2(ωg-ω2)2+4ξ2gω2gω2S0]
[S0]为地震谱强度.[ωg=19 rad/s],[ξg=0.65],[S0=0.015 54 m2/s3].
1)经典阶跃型调制函数,[a(t)=1 ].
2)Spanos-Solomos型调制函数[16]:
[a(ω,t)=2 ω5π t e-0.5×0.15+ω225π2t].
取5种工况,分别为[rb=0.5, rb=0.8, rb=1.5, rb=10, rb=∞].计算中步长取[τ=0.01 s].
①响应方差对比分析
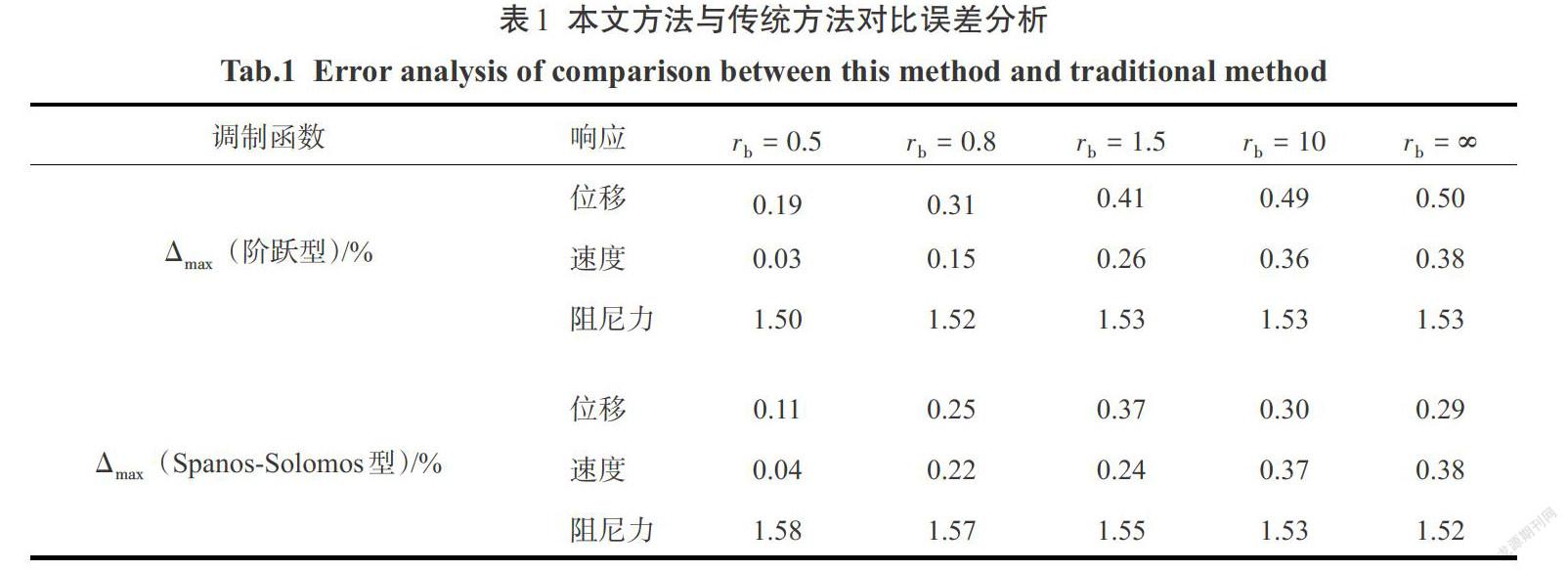
在上述两种非平稳地震激励下,本文方法与传统方法求出该系统在5种工况下的位移、速度和阻尼力对比的误差值如表1所示.
可以看出,本文方法所得响应方差误差较小,无论[rb]取多大值,位移与速度响应方差的最大误差[Δmax≤0.5%],阻尼力响应方差误差[Δmax]在[1.5%]左右,数值计算结果较为理想,从而验证了本文方法的精确性与可行性.
②结构及各阻尼构件的响应方差计算
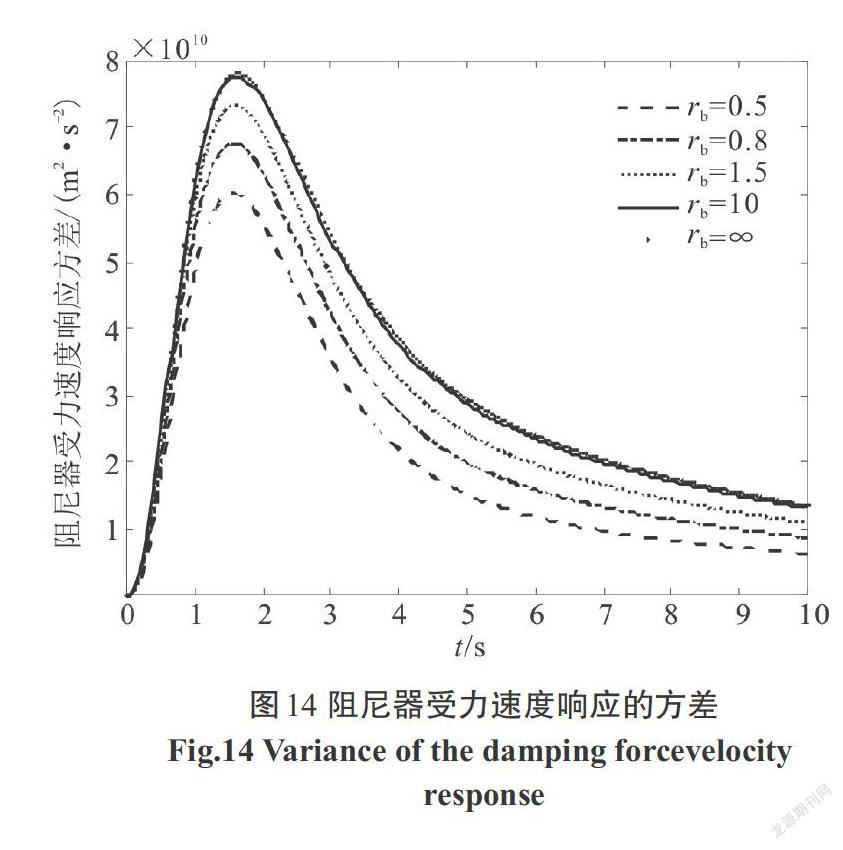
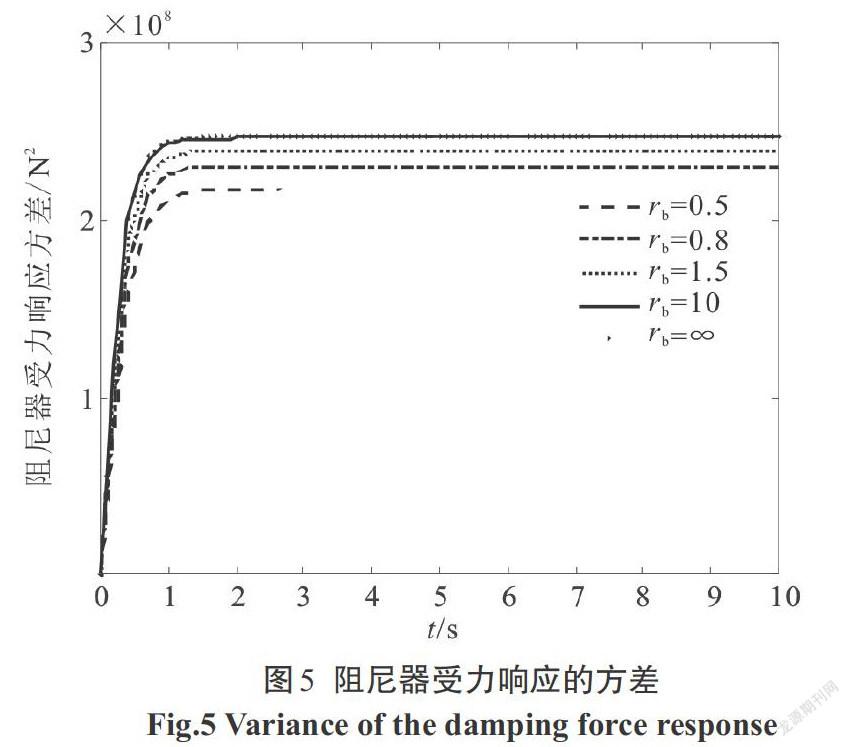
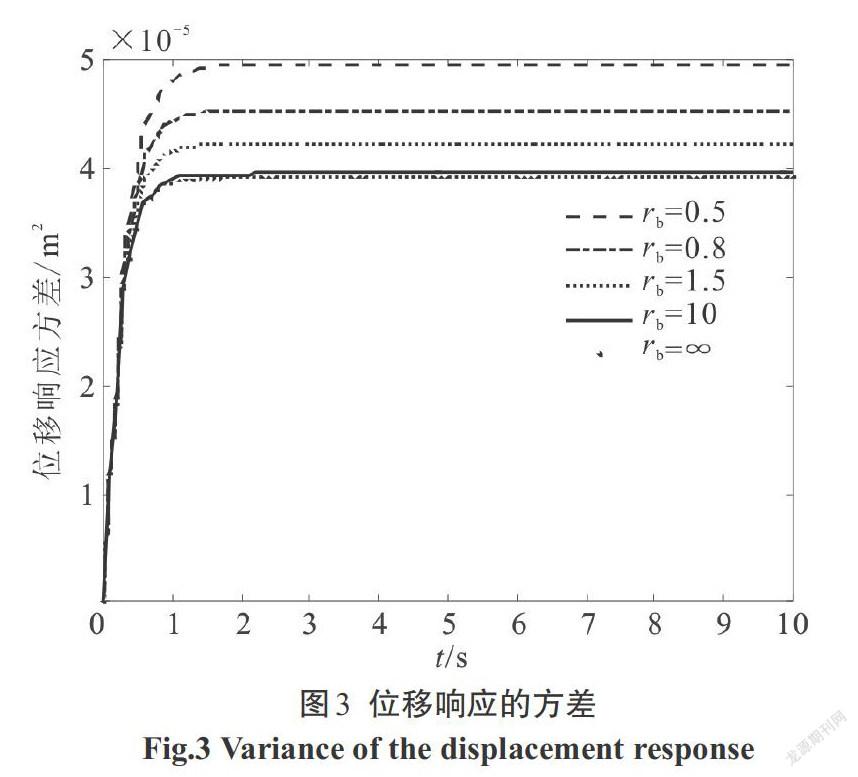
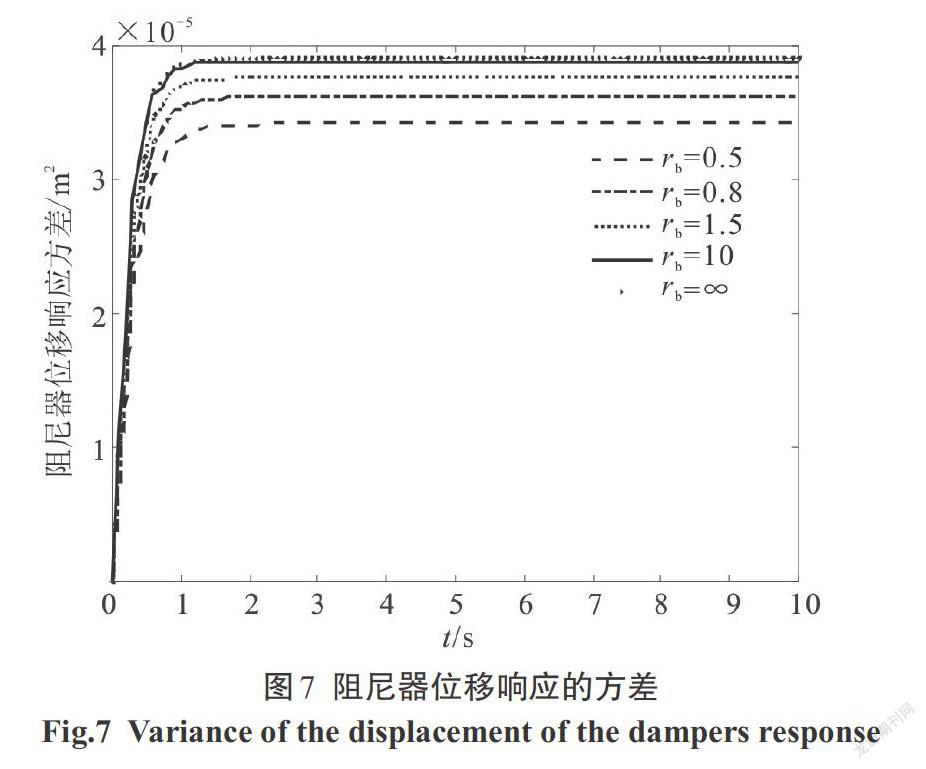
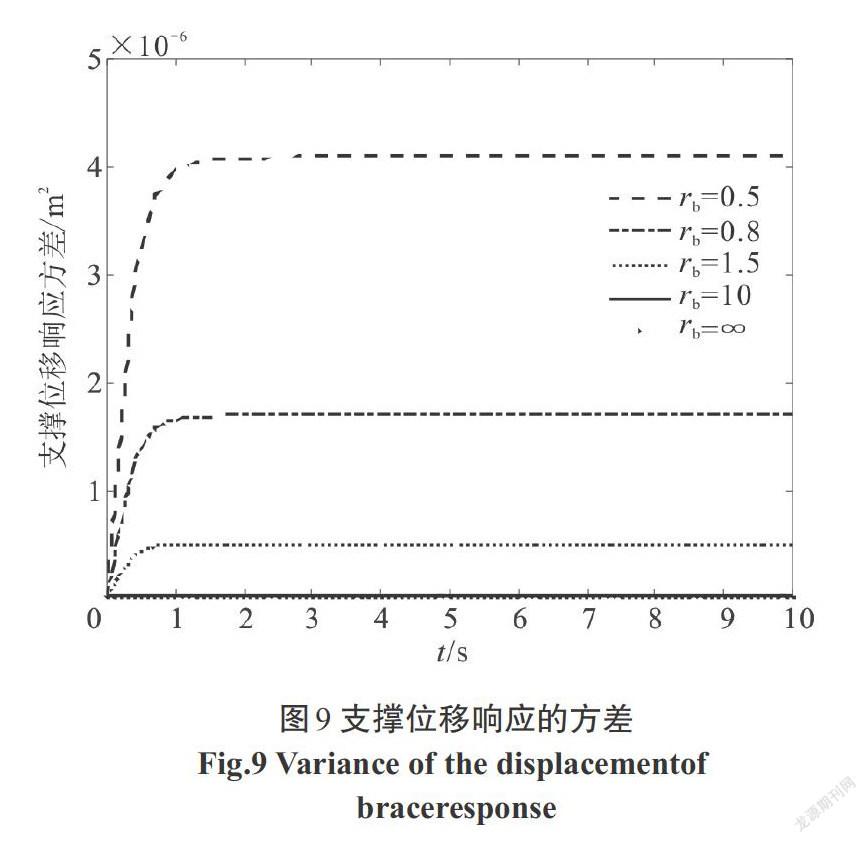
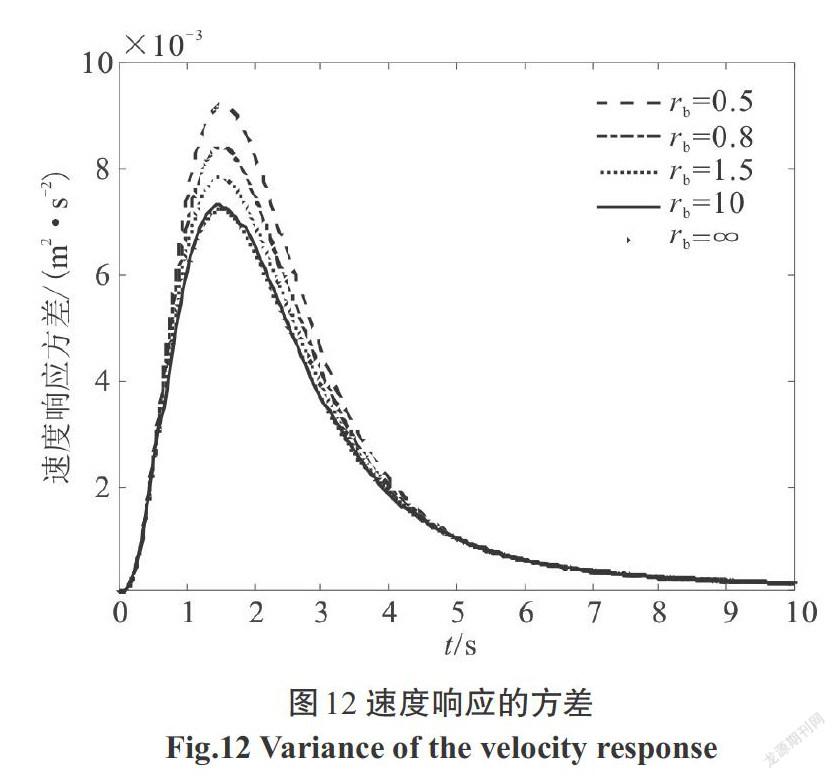
利用本文方法求出结构位移、速度,阻尼器受力、受力速度,阻尼器位移、速度,支撑位移、速度的响应方差,图像如下,阶跃型调制非平稳响应图像如图3—图10,Spanos-Solomos型调制非平稳响应图像如图11—图18.
以上两种调制非平稳随机地震激励下,对结构及各减震构件响应方差的数值分析可以看出:
1)支撑刚度[kb]对结构减震效果影响较大.在5种[kb]的影响下,随着支撑刚度[kb]的增加,结构的位移(对应图3、图11)、速度(对应图4、图12),支撑的位移(对应图9、图17)、速度(对应图10、图18)等响应方差均呈现减小趋势.但是当支撑刚度[kb≥10 k]后,结构位移和速度响应的减小量不大.即支撑刚度越大,减震效果越好,但是当支撑刚度足够大时,减震效果改善不明显且不够经济.
2)支撑位移和速度响应方差,与结构位移响应方差变化趋势保持一致,阻尼器位移和速度响应方差,与阻尼器受力响应方差变化趋势保持一致.支撑刚度[kb]越大时,阻尼器的位移、速度及阻尼器两端受力均越大,对应图5—图8和图13—图16可以看出.阻尼器的位移、速度和两端受力的大小,必然将影响构件的动力可靠度及性能.
4 结论
在六参数粘弹性阻尼耗能减震系统的非平稳随机响应分析中,化随机激励为虚拟激励,得出系统的响应的精细积分法响分析法,经分析得出如下结论:
1)本文方法与传统方法对比精度较高,验证本文方法的精确性与可行性,说明本文所获得的非平稳响应的解析解,对于六参数粘弹性耗能减震系统具有较好的工程适用性.
2)本文方法不仅可应用于此类耗能结构响应分析,而且可应用于各减震构件基于泊松过程的抗震动力可靠度分析,为虚拟激励-精细积分法开辟了新的应用领域.
3)支撑刚度的变化对结构和各减震构件的响应有很大影响,该研究对于系统中减震构件参数的选用具有一定的参考价值.
参考文献
[1] CHRISTOPOULOS C,FILIATRULT A. Principle of passive supplemental damping and seismic isolation[M]. Pavia,Italy:IUSS Press,2006.
[2] 王烨华,周云,丁鲲. 粘弹性阻尼减震结构研究与应用的新进展[J].防灾减灾工程学报,2006,26(1):109-121.
[3] CHANG K C,LIN Y Y. Seismic response of full-scale structure with added viscoelastic dampers[J].Journal of Structural Engineering, 2004,130(4): 600-608.
[4] MAZZA F,VULCANO A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers[J]. Earthquake Engineering and Structural Dynamics,2011,40(2):155-174.
[5] 李創第,刘鹏,葛新广,等. 六参数实用粘弹性阻尼器单自由度减震系统非平稳响应分析[J].广西科技大学学报,2018,29(2):110-118,125.
[6] 李創第,朱腾飞,柏大炼,等. 实用粘弹性阻尼器耗能结构非平稳地震响应的快速求解[J]. 广西科技大学学报,2018,29(4):94-102.
[7] PRIESTLEYN M B. Power spectral analysis of nonstationary random process[J]. Journal of Sound and Vibration,1967,6(1): 86-97.
[8] ERNESTO H Z,VANMARCKE E H. Seismic random vibration analysis of multi-support structiral systems[J]. Journal of Engineering Mechanics,1994,120:1107-1128.
[9] WILSON E L,KIUREGHIAN A D,BAYO E. A repiacement for the SRSS method in seismic analysis[J]. Earthquake Engineering and Structural Dynamics,1981(9):187-192.
[10] 林家浩,张亚辉. 随机振动的虚拟激励法[M]. 北京:科学出版社,2004.
[11] 林家浩,张亚辉,赵岩. 虚拟激励法在国内外工程界的应用回顾与展望[J].应用数学和力学,2017,38(1):1-8.
[12] 钟万勰. 结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136.
[13] 高强,谭述君,钟万勰. 精细积分方法研究综述[J]. 中国科学:技术科学,2016,46(12): 1207-1218.
[14] 林家浩,沈为平,威廉斯. 受演变随机地震激励结构的精细逐步积分法[J].大连理工大学学报,1995,35(5):600-605.
[15] 林家浩,张亚辉,孙东科. 受非均匀调制演变随机激励结构响应快速精确计算[J].计算力学学报,1997,14(1):1-8.
[16] LIN J H,ZHANG W S,MILLIAMS F W. Pseudo-exciation algorithm for nonstationary random seismic responses[J]. Engineering Structures,1994,16(4):270-276.
[17] SPAN P T D,SOLOMOS G P. Markov approximation to transient vibration[J]. Journal of Engineering Mechanies,1983,109(4):1134-1150.
Precise integration method for non-stationary seismic response
analysis of six-parameter viscoelastic energy dissipation system
LI Chuangdi, CHANG Mingjing, BAI Dalian, WANG Bowen
(School of Civil Engineering and Architecture, Guangxi University of Science and Technology,
Liuzhou 545006, China)
Abstract: For a six-parameter viscoelastic energy dissipation system, a precise analysis method of

