非对称管件内高压成形的仿真研究
罗建斌 黄煜 李健 王荣耀 张维烜





摘 要:非对称管件内高压成形工艺具有工序少、质量轻、抗弯模量大等优点.为研究非对称管件内高压成形规律,为实际生产提供预测和参考.根据理论公式确定主要工艺参数,借助非线性有限元方法进行仿真分析,研究直线、折线与梯形加载路径对非对称管件成形质量的影响,分析了补料量与整形压力对非对称管件成形质量的影响.结果表明,在内压折线加载路径下,补料量为16.000 mm,整形压力为90 MPa时能获得成形质量较好的管件.非线性有限元数值模拟方法可为非对称管件内高压成形工艺参数提供预测和参考.
关键词:内高压成形;非对称;加载路径;有限元模拟
中图分类号:U463.2 DOI:10.16375/j.cnki.cn45-1395/t.2019.04.005
0 引言
管材内高压成形以其减重、高强度和高刚度等优点,在航空航天、汽车等行业的板成形和零部件制造中发挥越来越重要的作用[1].我国汽车行业的快速发展对空心零部件的结构轻量化以及成形质量要求越来越高,管材内高成形技术正是适应于这样的要求而发展起来[2].管件内高压成形技术开始逐渐取代传统的冲压工艺,加速着国产汽车产业的技术革新[3].
自20世纪40年代以来,针对非对称空心截面结构件的内高压成形技术,国内外学者开展了研究.Chen等[4]针对变径管类零件在液压成形过程中厚度分布不均匀的问题,提出了一种有益褶皱与预成形相结合的方法.研究表明:加载路径对裂纹和起皱缺陷的形成起着重要作用,通过控制轴向进给与内压的关系得到最优加载路径.郎利辉等[5]借助仿真分析防锈铝变径管内高压成形过程中材料的合理流动趋势对最终成形结果的影响,应采用合理的工艺参数来控制皱纹的形成.林俊峰等[6]根据塑性力学理论计算出成形的初始内压,确定成形区间,然后调整不同的轴向补料量进行数值模拟,并根据数值模拟的分析结果确定最佳的补料量.袁安营等[7]用MSC.Marc有限元分析软件进行模拟分析,研究了变径管成形过程的基本变形特征与成形参数的影响规律.袁杰[8]用仿真分析的方法规划了成形加载路径,并对各种缺陷形式阐述了预防措施.然而,目前对管材内高压成形的研究多为起皱行为与轴向进给、内压两者的关系,忽略内压在不同加载路径下对管件内高压成形质量的影响,理论补料量与实际补料量的关系.
通过有限元模拟方法,管坯材料采用304不锈钢管坯,对带凹槽非对称管件进行内高压成形数值模拟.主要分析不同内压力加载路径对其成形性能的影响,不同补料量对管件壁厚值的影响,以及整形压力对管坯过渡圆角区域贴模情况的影响.
1 成形工艺分析
该非对称管件如图1所示,长度为118.900 mm,壁厚为1.500 mm,最大截面周长为251.200 mm,最小截面周长 159.500 mm.管件为两边非对称结构,成形区由六边形界面向圆形界面过渡.表面带凹槽结构,过渡半径较小,在传统工艺上难以一次成形.因此,采用内高压成形方法一次成形.
2 非对称管件仿真分析
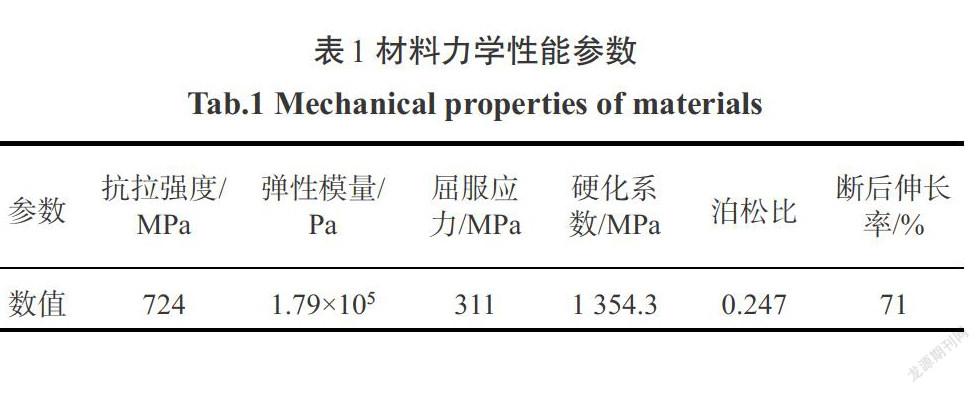
根据计算与非对称管件结构,选取SS304不锈钢,初始管坯长度180.000 mm、直径50.800 mm、厚度1.500 mm.通过单向拉伸实验获取其应力—应变曲线,经拟合得到其硬化指数n=0.41.选用的材料力学性能参数如表1所示.对零件进行建模,上下模具、左右推头以及管坯之间整体的装配关系及有限元模型如图2所示.采用4×4的平面四边形单元对管坯与模具进行网格划分,上下模具和左右推头均定义为刚性单元.上下模具网格单元数量为3 276个,左右推头网格单元数为930,管坯网格单元数为2 760.
3 内高压成形数值模拟分析
3.1 内压加载路径的影响规律
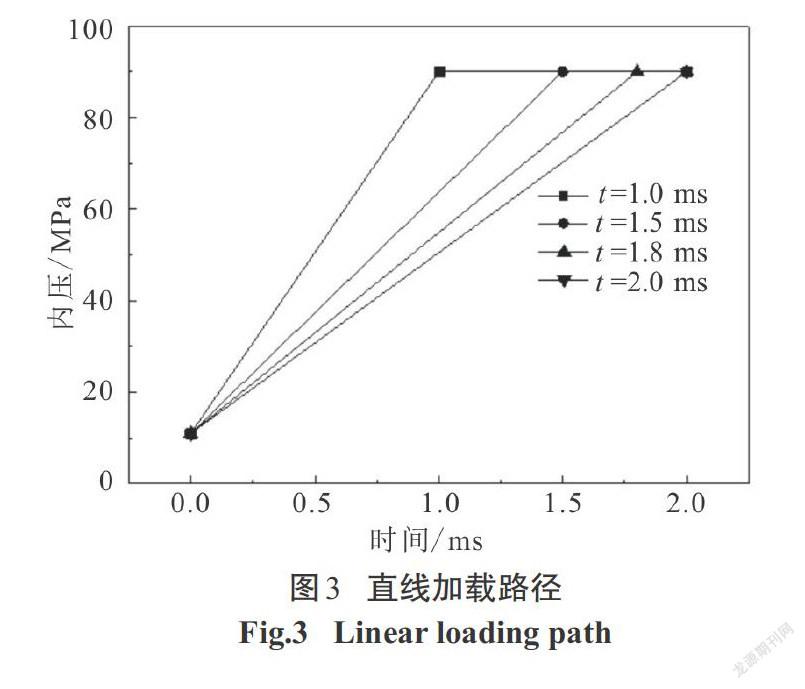
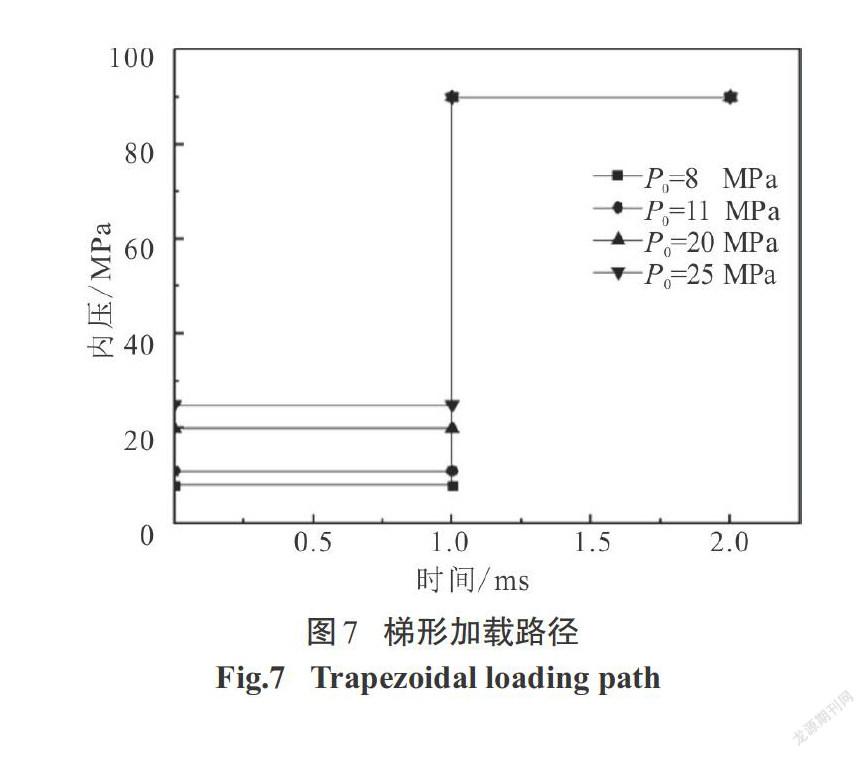
内压加载路径对管件成形质量至关重要,加载路径通常有3种加载方式:直线加载路径、折线加载路径和梯形加载路径.同样的初始压力与整形压力,在不同加载路径下管件成形最小壁厚相差较大.根据变形前后面积不变的条件计算出理论总补料量为40.000 mm,由公式[P=2tdσs]计算确定初始压力P0=11 MPa、最大整形压力 P2=90 MPa.
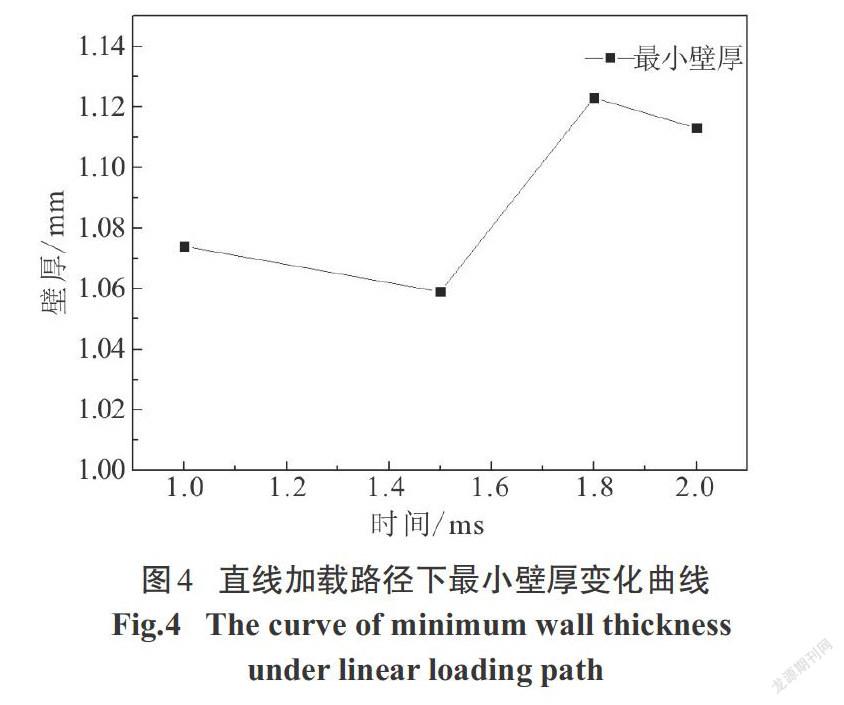
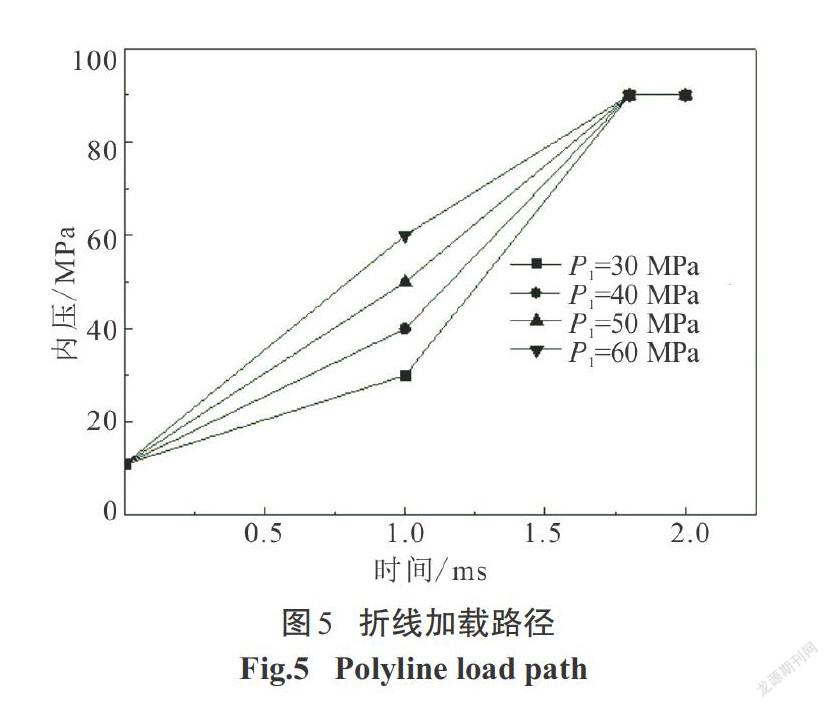
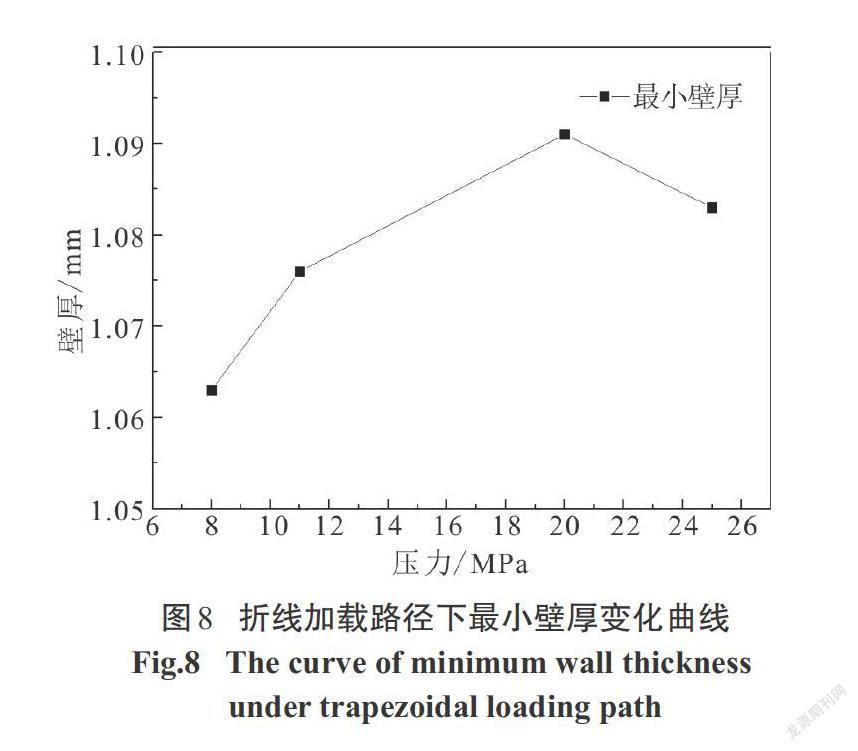
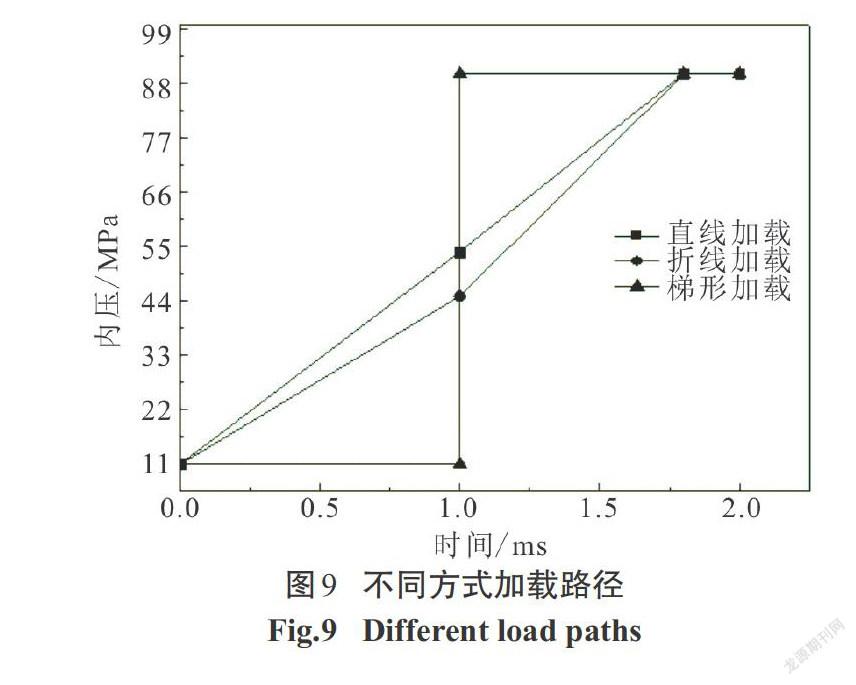
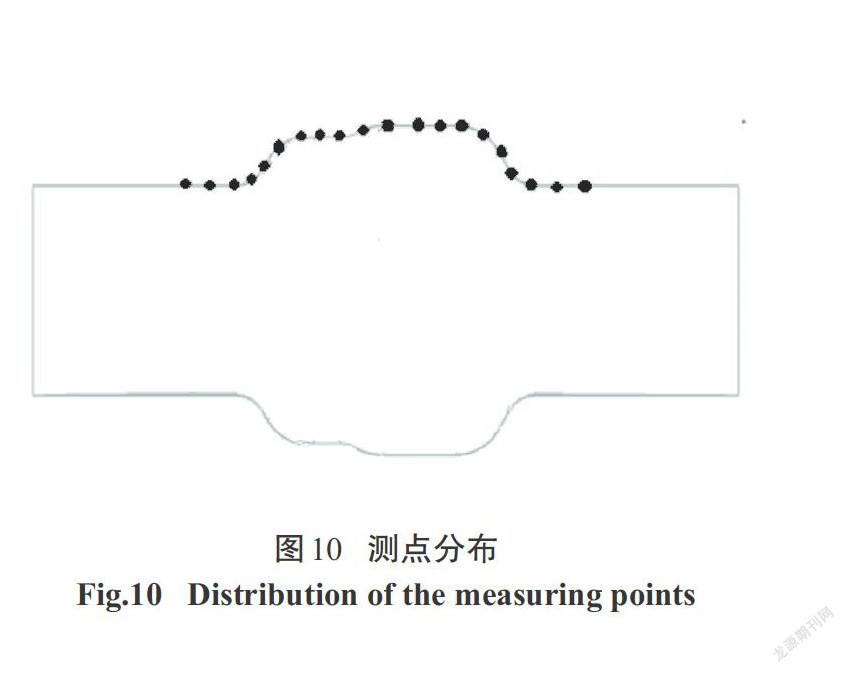
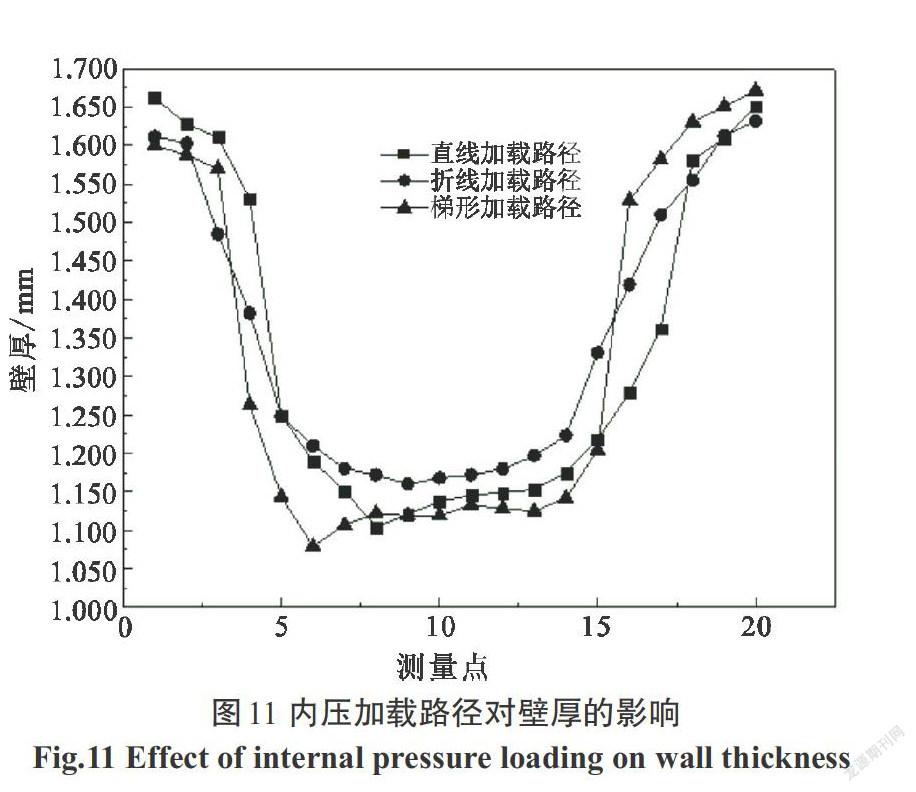
4种直线加载路径如图3所示,根据从初始压力P0=11 MPa至最大整形压力P2=90 MPa的加载时间t分为4种工况:t =1.0 ms、t =1.5 ms、t =1.8 ms、t = 2.0 ms.如图4所示:加载时间上升速率越大,成形最小壁厚值越小.但在t =2.0 ms的加载路径下,由于其加载速率过小,材料无法展平而失效.因此,对于直线加载路径,可以认为成形质量相对较优的路径为t =1.8 ms.4种折线加载路径如图5所示:初始压力P0=11 MPa、整形压力P2=90 MPa、中间拐点压力P1分别为30 MPa、40 MPa、50 MPa、60 MPa. 其中,P1=30 MPa、 P1=40 MPa、P1=50 MPa这3种加载路径均是前期加载速率小于后期加载速率.对于这3种工况成形結果最小壁厚值如图6所示:随着拐点压力P1的提高,最小壁厚增加,P1=40 MPa和P1=50 MPa时的最小壁厚相等.而当P1=60 MPa时,前期加载速率反而大于后期加载速率,此时,材料在快速胀形时无法补充,壁厚反而减薄.因此,对于折线加载路径,可以认为成形质量相对较优的路径为P1=40 MPa.4种梯形加载路径如图7所示,在1 ms时间内保持初始压力P0不变而阶跃为整形压力P2=90 MPa进行保压.根据初始压力P0的大小分为4种工况:P0=8 MPa、P0=11 MPa、P0=20 MPa、P0=25 MPa.由图8可知,最小壁厚的分布随着P0值的增加,最小壁厚值首先增加,P0=20 MPa时达到最大值,但当P0=25 MPa时,最小壁厚值反而有所下降.因此,对于梯形加载路径,成形质量相对最优的工况为P0=20 MPa.根据上述所得到的成形质量相对最优的直线加载路径、折线加载路径以及梯形加载路径的仿真结果,进行3种工况的比较,3种加载路径如图9所示.为了进一步对3种不同加载路径的成形质量进行比较分析,沿着如图10所示的某一轴线剖开,从距离左端32.000 mm处开始,均匀间隔5.000 mm,共取20个测点.不同加载路径下各测点的壁厚分布如图11所示.从图11中可以看出,在内压直线加载路径下,最小壁厚值达到了1.104 mm.直线加载路径下左端圆角处壁厚产生堆积最为严重,达到了1.680 mm,但成形区壁厚较折线加载路径减薄大.这是因为在成形初期压力一直呈直线上升形式,前期在较大压力下补料顺利进行但材料无法累积,以致于在后期胀形补料不及时壁厚减薄严重.梯形加载路径下,初期压力保持11 MPa不变,后期整形压力升至90 MPa.从图11中可以看出,两端圆角处材料堆积较少,成形区减薄最为严重,最小壁厚值为1.091 mm.由于初期压力无变化在轴向进给作用下材料产生聚集,然后压力迅速升至90 MPa.材料累积在力作用下迅速展开,快速胀形时已无法补料,壁厚减薄较大.内压折线加载路径下,其成形结果最小壁厚为1.158 mm,相较其他两种加载方式成形的壁厚值分布更加均匀.前期压力上升速度较小而聚集材料,后期压力上升速度较大而能将前期聚集的材料在胀形过程中充分展开,因此,成形壁厚减薄情况能得到有效控制,成形效果最好.
3.2 补料量对成形结果的影响
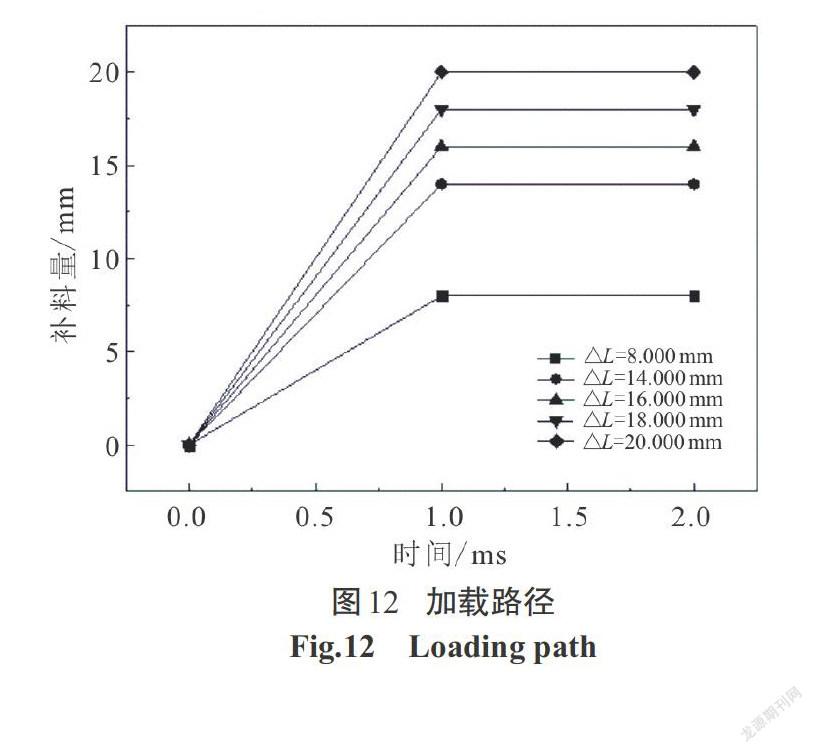
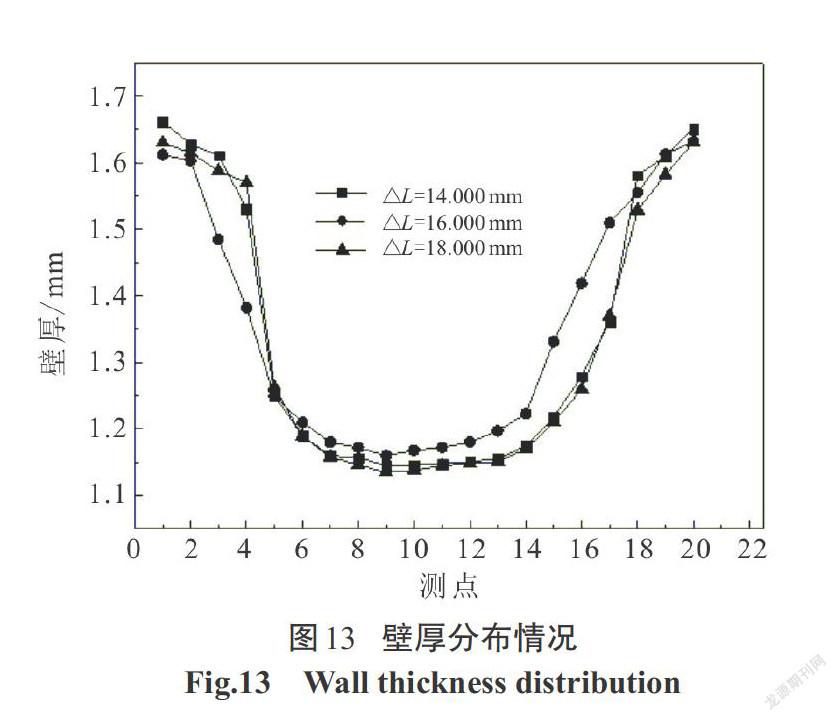
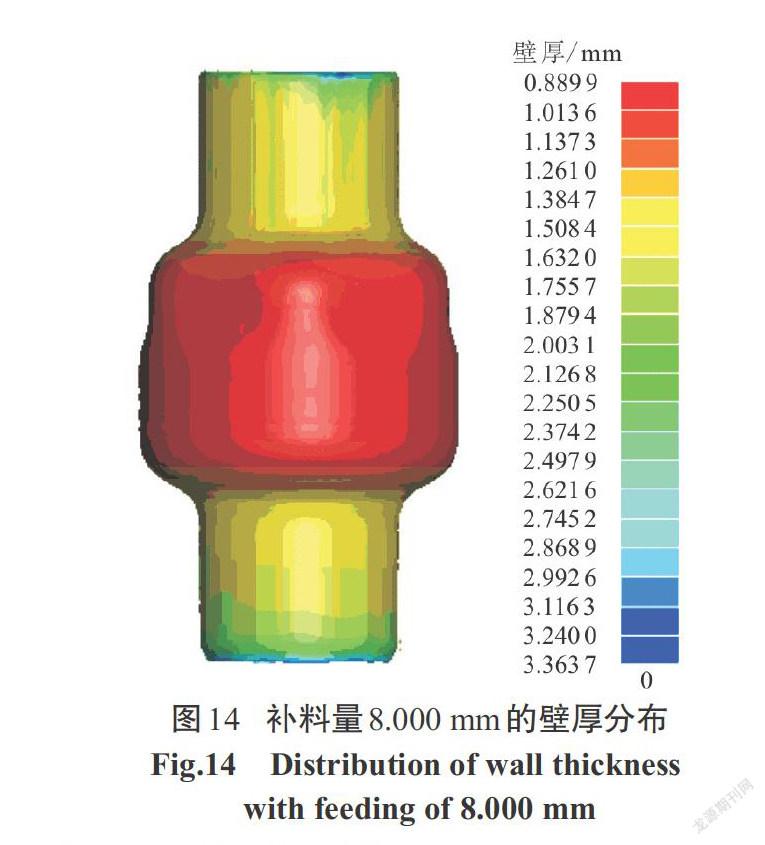
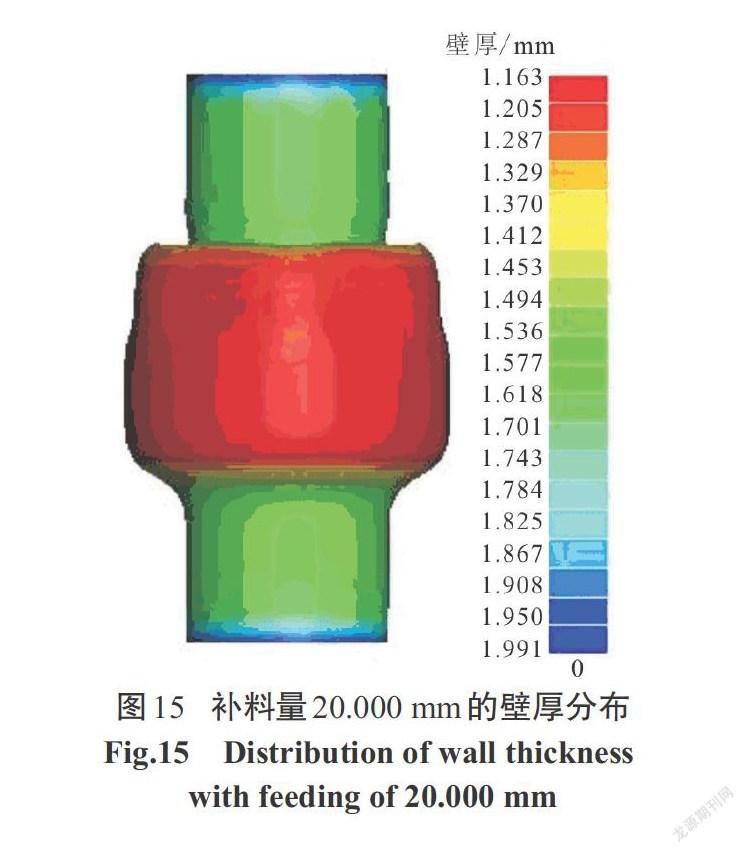
经变形前后面积不变原理计算出总补料量为40.000 mm,在实际工艺中,由于金属流动性和摩擦力的影响,并不能达到理想的补料量.推头进给过多则会产生死皱的缺陷形式.因此实际补料量小于理论补料量,一般为理想补料量的60%~80%.分别设计左右推头的补料量 △L各为8.000 mm、14.000 mm、16.000 mm、18.000 mm、20.000 mm,加载路径如图12所示.各测点壁厚分布情况如图13所示.从该图中可以看出,轴向进给为14.000 mm、18.000 mm时,在圆角过渡处壁厚增大但成形区的壁厚较进给为16.000 mm壁厚值大,材料在圆角过渡处累积较多,但成形区壁厚相对于进给为16.000 mm减薄较大.过多与过少的补料量对壁厚都会产生影响,如图14所示补料量为8.000 mm的成形壁厚结果图,最小壁厚值为 0.889 mm,在实际生产中管件因补料不足壁厚减薄严重,管件已失效破裂.如图15所示,左右补料量各为20.000 mm时,最小壁厚为1.163 mm,但由于轴向进给过多右边圆角过渡处产生严重凹陷,失效形式为死皱.在壁厚分布图中补料量为18.000 mm在成形后期时左右端头发生严重材料堆积,由于成形后期管坯已开始贴模产生较大摩擦力使材料未能继续向胀形区流动,使得端头壁厚增厚严重.在补料量16.000 mm下,补料充分最终成形效果较好,管件成形区壁厚分布均匀,最大减薄率为22.6%.
3.3 整形压力对圆角影响
在管件成形后期,管件大部分已成形,无轴向进给,此时需要加大压力使圆角过渡处与模具贴合.整形压力随着圆角过渡处半径减小而增加,经公式估算得出整形压力P2约为74 MPa.研究表明整形压力与材料屈服强度有关,约为材料屈服强度的1/10~1/4,即35 MPa~87 MPa.选取整形压力为变量,其他参数不变,整形压力P2分别为 70 MPa、80 MPa、90 MPa、100 MPa时,成形结果如图16所示.整形压力P2=70 MPa时最小壁厚为1.160 mm,但圆角过渡处材料仅部分贴模,整形压力不足,凹角无法展平;整形压力为P2=80 MPa时,管坯部分贴模,管坯与模具之间还存在间隙,壁厚与P2=70 MPa相差不大,为1.159 mm.整形压力在P2=90 MPa(约为材料屈服强度1/4时),最小壁厚值为1.158 mm,圆角过渡处管坯与模具完全贴模.整形压力为P2=100 MPa时管材最小壁厚仍为1.158 mm,因此整形压力P2=90 MPa能满足工艺需要.
4 结论
采用有限元方法,针对非对称管件,对内压加载路径、补料量以及整形压力对成形质量的影响进行了数值模拟分析.主要结论如下:
1)不同内压加载路径对非对称管件内高压成形的壁厚分布影响较大.对比直线、折线和梯形等3种加载路径的分析得出,折线加载路径的成形效果最佳,壁厚分布均匀,可有效地控制管件壁厚的减薄率.
2)由于模具与构件之间的摩擦作用,很难实现理论补料量的完全补给.通过仿真分析可知,补给量为理论补料量的80%时,成形效果最佳,最小壁厚值最大,且非对称管件的左右端头没有产生材料折叠堆积.
3)管件圆角位于补料区与胀形区的过渡处,在后期无轴向补给的情况下,整形压力过低时无法保证管坯与模具的完全贴模,整形压力为90 MPa时能满足贴模的工艺要求.
参考文献
[1] 苑世剑,王小松. 内高压成形技术研究与应用新进展[J]. 塑性工程学报,2008,15(2):22-30.
[2] 秦文东,林贤坤. 一种异型管件内高压成形规律仿真研究[J]. 广西科技大学学报,2018,29(1):20-24.
[3] HWANG Y M,LIN Y K. Analysis of tube bulge forming in an open die considering anisotropic effects of the tubular material[J]. International Journal of Machine Tools & Manufacture,2006,6(15):41921-41928.
[4] CHEN Y C ,CHUANG C Y ,LEE M F . Process parameter with high expansion rate of SUS304 tube hydroforming[J]. Procedia Engineering,2014,81:2230-2236.
[5] 郎利輝,苑世剑,王仲仁,等.防锈铝变径管内高压成形过程数值模拟[J]. 中国有色金属学报,2001,11(S2):211-216.
[6] 林俊峰,李峰,韩杰才,等. 管件液压成形中加载路径的确定方法研究[J]. 材料科学与工艺,2009,17(6):840-843.
[7] 袁安营,王忠堂,梁海城,等. 变径管内高压成形有限元模拟[J]. 机械工程与自动化,2006(4):1-3.
[8] 袁杰. 基于内高压成形技术的某SUV车型发动机横梁的实验与仿真[D].柳州:广西科技大学,2015.
Simulation study of asymmetric tube hydroforming
LUO Jianbin,HUANG Yu,LI Jian,WANG Rongyao,ZHANG weixuan
( Guangxi Key Laboratory of Automobile Components and Vehicle Technology(Guangxi University of Science and Technology),Liuzhou 545006,China)
Abstract: The asymmetric hydroforming process has the advantages of less working procedure and higher quality bending modulus. With the help of nonlinear finite element method,the main process parameters are determined according to the theoretical formula. On this basis,the influences of straight line,broken line and trapezoidal load path on the forming quality of asymmetric pipe fitting are studied. Secondly,the influence of feeding and shaping pressure on the forming quality of asymmetric pipe fitting is analyzed. The results show that the tube with good forming quality can be obtained under the loading path of internal pressure polyline with the filling amount of 16 mm and shaping pressure of 90 MPa. The numerical simulation method of nonlinear finite element method can provide prediction and reference for determining the process parameters of asymmetric tube in hydroforming.
Key words:hydroforming;asymmetric;loading path;finite element simulation
(責任编辑:黎 娅)

