设计开放习题，培养思维品质

李勇军

开放型习题是指条件不完备或结论不确定的习题。开放型习题的核心是开放学生思维。在数学课堂教学中恰当设计开放习题，不仅有利于学生知识的掌握，而且有利于培养学生思维的深刻性、批判性、灵活性、全面性甚至创造性。

一、设计结论多元型开放题，培养学生思维的深刻性和多维性

结论多元型开放题是指答案不唯一的习题。解题时要利用已有的知识，结合有关条件，从不同的角度对问题作全面、深入分析，通过概括归类，才能得出正确结论，从而培养学生思维的深刻性和多维性。

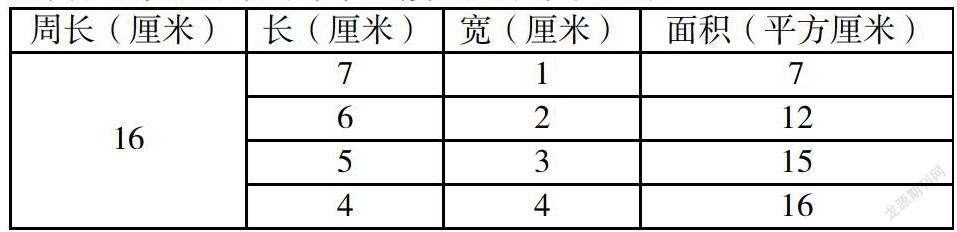
如：学习“长方形和正方形的面积”时，学生对“面积”和“周长”的意义及计算方法容易混淆，以致解题时出现错误，在学生基本掌握了面积计算方法后。设计这样的习题：已知一个长方形的周长是16厘米，求它的面积是多少？因长方形的长和宽不确定，所以有多种答案。引导学生用16厘米长的绳子在钉子板上围不同长和宽的长方形，分别算出面积，如下表：

解答后引导分析，得出：周长相同的长方形，长和宽不一定相同，面积大小也不一定相同;长方形的长、宽相等时（正方形），面积最大。这样通过学生主动地学习、研究，加深了对面积和周长的意义的理解及计算方法的掌握，同时也培养了学生思维的深刻性，提高了解决问题的能力。

又如：学习了“质数和合数”后，出示：一个两位数，已知十位上的数字是2，个位上是a，判断这个是质数还是合数？由于个位数字不确定，可能是0到9这十个数字中的任何一個，所以无法判断。学生经过讨论得出：如果这个两位数能被2、3、5这三个数中的任意一个数整除，那么这个数是合数，否则是质数。也就是个位数字是2、4、6、8、0（能被2整除），或是1、4、7（能被3整除），或是0、5（能被5整除）时，即个位数字是1、2、4、5、6、7、8、0这8个数字中的任何一个数时，这个两位数是合数;个位数字是3或9时，这个数是质数。学生通过解答，对“质数和合数”及“能被2、3、5整除的数的特征”这两部分知识加深了理解，同时也训练了深入思考、全面分析的能力。

二、设计条件型开放题，培养学生思维的批判性和缜密性

条件型开放题包括条件多余或条件隐藏的开放习题。

1.条件多余的开放型习题是习题中把有用和无用条件混在一起，产生干扰因素，这就需要在解题时，认真分析条件与问题的关系，充分利用有用条件，舍弃无用条件。学会排除干扰因素，提高学生的鉴别能力，从而培养学生思维的批判性。

如：商店原来有一些玩具，卖了8个，还剩16个，又运来50个，现在有多少个？由于受封闭式解题习惯的影响，学生往往会产生一种凡是题中出现的条件都要用上的思维定势，不对题目进行认真分析，错误地列式为：50+16-8或8+16+50。做题时引导学生联系实际生活分析，使学生明白：求现在玩具的个数实际上是求还剩的和又运来的一共有多少个，这里“卖了8个”是与解决问题无关的条件，正确的列式是：16+50。

经常进行此类习题的练习，可防止学生滥用条件，有利于培养学生思维的批判性，提高学生明辨是非、去伪存真的鉴别能力。

2.条件隐藏是指解题所需的某些条件隐藏在题目的背后，如果不认真审题容易遗漏。在解题时既要考虑问题及明确的条件，又要考虑与问题有关的隐藏着的条件。这样有利于培养学生认真细致的审题习惯和思维的缜密性。

如：用布做一个长9分米、宽6分米的面粉袋，至少需要布多少平方分米？ 题中隐藏面粉袋有“两层”这个条件，大部分学生错误地列式为：9×6，正确列式应为：9×6×2。设计此类习题，要让学生认真分析题意，找出题中的隐藏条件，使学生养成认真审题的良好习惯，有利于培养思维的缜密性。

三、设计情境型开放题，培养学生思维独立性和创造性

情境型开放题是由答题者依据要求独立创设条件和问题的题型。通过学生自己创设灵活多变的条件或问题情境，使学生思维独立性和创造性得到培养和发展。这类题有部分自编和全部自编两种情况。

1.由学生自编部分条件和问题的习题，如：一班有31张彩色纸，糊灯笼用去7张。把它编成两步计算的应用题，再解答。此题只提供了两个条件，其它条件和问题由学生自编，学生根据自己的生活经验可补充不同数量关系的条件和问题：①又买来15张，现在有多少张？②剩下的做了8个航模飞机，每个航模飞机用彩色纸多少张？③做小旗用去20张，还剩多少张？

2.根据要求完全由学生创设条件和问题。如：六年级总复习时，复习工程问题这部分。可让学生编已知工作总量和工效求时间的应用题，学生能编出：①一台织布机每小时织布3米，24米布需要多少小时？②两个编篮小组合编1600个竹篮，第一组每天编18个，第二组每天编14个，两组同时编，多少天能编完？③铺一条长1050米的路，甲队单独铺需要35天，乙队单独铺需要21天，由甲队先铺140米后，两队合铺，还需要多少天才能铺完？④甲乙两地的铁路长1325千米，一列火车从甲地开往乙地，已经行了3/5，剩下的路程如果每小时行88千米，经过几小时到达乙地？

创设应用题情境这类习题有较强的主观性，创设条件或问题情境因人而异，在编题创设情境的过程中，能反映出学生对数量关系本质的掌握情况;在这个过程中，学生的思维具有明显的独立性、新颖性，创造性、合理性思维品质能得到培养和发展。

四、设计一题多解型开放题，培养学生思维的灵活性和全面性

一个问题，答案唯一，但有几种解题思路。学生通过多角度思考、求解，从而培养思维的广阔性和灵活性。

如：张师傅加工一批零件，7.2小时刚好完成这批零件的3/5。照这样的速度，还需要几小时才能加工完？这道题根据数量之间的关系，从不同的角度思考，解法有：

①分数法：7.2÷3/5-7.2;

②倍比法：7.2×[（1-3/5）÷3/5]或7.2÷[3/5÷（1- 3/5）];

③比例法：设还要x小时才能到乙站，则有（1-3/5）：x =3/5：7.2;

④工程法：1÷（3/5÷7.2）-7.2。

然后引导学生比较哪种方法最简便，哪种思路最简捷。

又如，学习了比较分数大小后，出示：“比较4/7 和5/11的大小，你能想出多少种方法？”学生会想出不同的方法：1.化成同分母分数比较;2.化成同分子分数比较;3.化成小数比较;4.画图比较;5.借助中间量1/2比较（4/7比 1/2多，而5/11比1/2少）。

这类题可以给学生最大的思维空间，学生从不同的角度分析问题，探究数量间的相互关系，并能从不同的解法中找出最简捷的方法，提高学生初步的逻辑思维能力，从而培养学生思维的广阔性和灵活性。

开放型习题，解题时由于没有现成的解题模式，往往需要从多个不同角度进行思考和探索，且有些问题的答案是不确定的，因而能有效激发学生丰富的想象力和强烈的好奇心，充分调动学生学习的积极性和主动性。在数学课堂教学中，坚持设计开放型习题，训练学生数学思维这条主线，学生的良好思维品质能得到有效培养和发展。

（作者单位：四川省乐山市市中区苏稽镇新桥小学）