差异化定价视角下高校收费标准数学模型研究
李琰


摘要:我国普通高等院校的收费问题一直以来都是热点问题,如果学费过高,部分家庭无力支付,容易引发社会问题;如果学费过低,部分学校会出现财政收支问题,影响教学质量与办学效果。因此,保证高校最低的办学费用,让学生接受高等教育具有重要的现实意义。本文借助相关统计数据,从地区、高校层次、高校类型、专业四个不同的维度对“差异化定价”进行概念界定,以现有的学费定价经验为基础,构建数学模型,以期协调好学费标准制定过程中各利益相关方的关系。
关键词:差异化定价;收费标准;数学模型
高等教育事业与国家人才培养、科技水平、创新能力的提升、社会的发展关系密切,需要注意的是,高等教育不属于义务教育,经费来源在世界各国都是由政府财政划拨、学校自行筹集、社会捐赠以及招生收入等款项组成。高校收费是一个复杂的问题,涉及到万千学子及家庭。1996年12月,我国正式颁布《高等学校收费管理暂行办法》,学费标准依据每年单个学生教育培养成本的特定比例确定的,且明确规定高校收费标准不得超过其25%。1999年,我国正式实施高等教育收费政策。近些年来,高等教育收费标准总体呈增加趋势,引起了社会各方的广泛关注。因此,收费标准是否符合我国国情以及广大居民的利益是高等教育实践面临的重要问题。
一、问题背景分析
(一)高校收费构成
一直以来,高等院校的收费标准问题是社会热点,自1997年实行高等院校收费政策以来,我国普通高校的办学规模实现了极大的发展,高等教育实现大众化与多元化。现阶段,我国的高校收费标准存在一定的问题,一定程度上影响到了部分学生及其家庭与社会的发展、稳定,成为重大的民生问题。高校收费涉及到广大学子及其家庭,如果收费过高,部分学生家庭支付压力过大,如果收费过低,高校的收入就会受到影响,教学质量得不到保障,不利于学生的求学以及学校的发展。
目前来看,我国高校的主要收入来源有以下两个:①国家财政拨款;②银行贷款。对于大多数学生而言,就学资金主要来自家庭教育投入,高校与学生个体之间的收入、支出关系如图l所示。由图可知,高校通过向学生收取教育服务费用来承担其教育成本与运营需要。如何合理收取教育服务费用、收取多少,需要一个合理的计算标准,综合考虑多重要素对高校收费标准的影响。
(二)差异化定价概念内涵
我國高等院校收费标准确定的过程中,需要依据特定地区的实际情况进行适当调整。在实践过程中,我国各地区的普通高校的收费标准相差不大,地区、高校层次、高校类型、专业的收取标准基本一致,没能体现出不同区域、学校类别、专业以及学生家庭承受能力等方面存在的客观差异。
现阶段,我国高等教育已经由单纯的规模增长转向了质量的提升,对于教育公平的诉求也更加强烈。在新的高等教育发展背景下,市场经济发展的客观规律以及高等教育资源的优化配置要求高校收费标准需要实现地区发展水平、学校、专业类别等条件的差异化表达。
不同地区、不同类别的高等院校的教育成本是存在差异的,从经济学供需理论来看,产品价格会影响其供需。高等院校的教育服务可以看作是一种公共产品,对高校收费进行差异化定价,对高等教育服务的优化配置具有重要的现实作用。
综上,本文所述的差异化定价是指根据不同区域、学校、专业、居民收入与消费能力来确定普通高等院校的学费,推行差异化、科学合理的收费标准,促进高等教育服务资源的合理配置,实现教育公平。
二、高校收费模型构建
借鉴国外已有的学费定价模式,可以尝试构建高等院校收费标准的差别定价模型,具体要求如下:
1.家庭承受能力前置考虑
在制定高校收费标准时,教育主管部门要注重教育成本核算标准的多层设计,优先考虑不同收入水平家庭学生的承担能力,根据不同的收入水平实施弹性定价机制。
2.不同地区差异化
我国的地区发展不同步,经济水平、物价水平等存在较大差异,因此高等院校的教育成本水平也存在区域性差异。在部分经济发达地区,所制定的收费标准要高于经济欠发达地区。
3.考虑学校、专业类别的差异
不同类型、等级的学校以及不同专业的收益率是不同的,对于一些办学水平高、基础设施更完善的大学要制定更高的收费标准。同时,某些专业的教学成本、收益率较高,因此制定的学费标准要略高于其他专业,比如材料化学、珠宝设计等。
普通高等院校收费标准的制定具有一定的标准,需要综合考虑多角度的要素,考虑到不同要素之间的相互影响。综上,本文选取高校类型、地区经济发展水平、家庭收入、专业特点等影响要素,制定符合教学实际的高等院校差异化定价模型。
(一)基本模型
本模型中的高校收费标准由以下两部分组成:①基本费用:与教育服务的提供量无关的费用;②与教育服务量直接相关的费用。教育费用平均价格为:
式中,C0表示固定成本,C1为边际成本且保持不变,A为高校学生总数,X1为教育服务的消费量。
我国发展的地区差异较大,这就造成了不同的地区的教育成本不同,标准无法统一。为了便于模型的构建,本文所构建的模型采用国家高等教育总投入R与高校学生总数S的比值C2来表示单个学生的培养成本,即C2 =R/S。
根据高校收费要素的构成,可以测算高等院校收费的平均值为:
P1=(1-x)r.b+x.C2.X
式中,x表示权衡系数,是一个常量;r表示所有家庭的平均收入,b表示学杂费用与人均国民生产总值的比值;C2为单个学生的培养成本;X表示单个学生的培养成本与学费的比值。在上述表达式中,前半部分表示基本费用,后半部分表示按照一定比例的单个学生培养成本所需收取的学费。
(二)差异化定价模型
上述表达式揭示的是一般形式下的高校收费标准模型,在此基础上,本文将高校类别、生源地经济发展水平、不同专业的收益率加入到模型中。
1.高校综合实力(W)
高校综合实力是教学水平、教学人员素质、教学质量、学生学习成本等要素的综合反映。一般情况下,综合实力(W)与教育成本C(W)以及教育收益F(W)呈正相关。在构建高校综合实力(W)的函数模型时,需要参考武书连的中国大学排行榜中的各高校得分(S)。需要注意的是,由于各高校之间的得分差距较大,甚至出现数10倍的差距,因此对该指标进行处理,通过函数拟合,可以近似得到高校综合实力(W):
式中,Si表示不同高校的得分,n表示参评高校总数。
2.生源地经济发展水平(G)
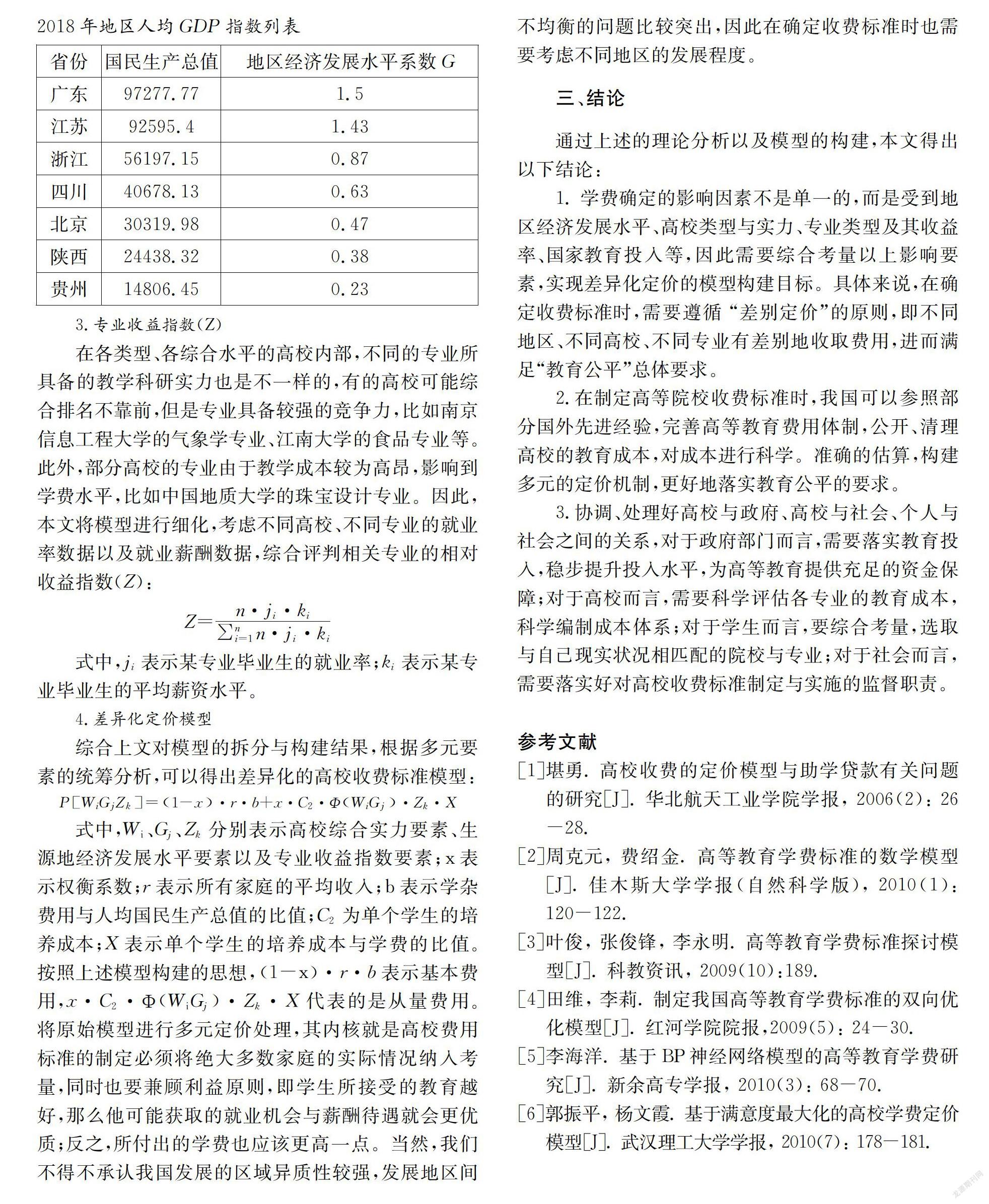
我国各地区之间发展程度不一,差距比较大,不同地区的国民生产总值、人均国民生产总值等经济指标差异较大,这也就导致了居民收入水平以及消费水平的差距,所能承受的高等教育费用也不一样。假设学费是关于人均GDP(gi)的函数,那么该地区的人均GDP指数(G)的函数表达式为:
Gi=gi/g
式中,g表示全国人均GDP水平。2018年地区人均GDP指数列表
3.专业收益指数(Z)
在各类型、各综合水平的高校内部,不同的专业所具备的教学科研实力也是不一样的,有的高校可能综合排名不靠前,但是专业具备较强的竞争力,比如南京信息工程大学的气象学专业、江南大学的食品专业等。此外,部分高校的专业由于教学成本较为高昂,影响到学费水平,比如中国地质大学的珠宝设计专业。因此,本文将模型进行细化,考虑不同高校、不同专业的就业率数据以及就业薪酬数据,综合评判相关专业的相对收益指数(Z):
式中,Wi、Gi、Zk分别表示高校综合实力要素、生源地经济发展水平要素以及专业收益指数要素;x表示权衡系数;r表示所有家庭的平均收入.b表示學杂费用与人均国民生产总值的比值;C2为单个学生的培养成本;X表示单个学生的培养成本与学费的比值。按照上述模型构建的思想,(1-x).r.b表示基本费用,x·C2.西(WiGi).Zk.X代表的是从量费用。将原始模型进行多元定价处理,其内核就是高校费用标准的制定必须将绝大多数家庭的实际情况纳入考量,同时也要兼顾利益原则,即学生所接受的教育越好,那么他可能获取的就业机会与薪酬待遇就会更优质;反之,所付出的学费也应该更高~点。当然,我们不得不承认我国发展的区域异质性较强,发展地区间不均衡的问题比较突出,因此在确定收费标准时也需要考虑不同地区的发展程度。
三、结论
通过上述的理论分析以及模型的构建,本文得出以下结论:
1.学费确定的影响因素不是单一的,而是受到地区经济发展水平、高校类型与实力、专业类型及其收益率、国家教育投入等,因此需要综合考量以上影响要素,实现差异化定价的模型构建目标。具体来说,在确定收费标准时,需要遵循“差别定价”的原则,即不同地区、不同高校、不同专业有差别地收取费用,进而满足“教育公平”总体要求。
2.在制定高等院校收费标准时,我国可以参照部分国外先进经验,完善高等教育费用体制,公开、清理高校的教育成本,对成本进行科学。准确的估算,构建多元的定价机制,更好地落实教育公平的要求。
3.协调、处理好高校与政府、高校与社会、个人与社会之间的关系,对于政府部门而言,需要落实教育投入,稳步提升投入水平,为高等教育提供充足的资金保障;对于高校而言,需要科学评估各专业的教育成本,科学编制成本体系;对于学生而言,要综合考量,选取与自己现实状况相匹配的院校与专业;对于社会而言,需要落实好对高校收费标准制定与实施的监督职责。
参考文献
[1]堪勇.高校收费的定价模型与助学贷款有关问题的研究[J].华北航天工业学院学报,2006(2):26- 28.
[2]周克元,费绍金,高等教育学费标准的数学模型[J].佳木斯大学学报(自然科学版),2010 (1):120 -122.
[3]叶俊,张俊锋,李永明,高等教育学费标准探讨模型[J].科教资讯,2009(10):189.
[4]田维,李莉,制定我国高等教育学费标准的双向优化模型[J].红河学院院报,2009(5):24-30.
[5]李海洋.基于BP神经网络模型的高等教育学费研究[J].新余高专学报,2010(3):68-70.
[6]郭振平,杨文霞,基于满意度最大化的高校学费定价模型[J].武汉理工大学学报,2010(7):178-181.

