不确定因素对生猪价格的预测模型及应用

祁小凡

摘要：近期猪肉价格在国内一直呈增长趋势，造成了整体市场价格的动荡，给市民日常生活带来不小影响，有序平稳的市场价格离不开政府部门的调控和监管。基于此，本文针对不确定因素下生猪的价格问题进行了研究预测，研究以乐山市市中区华联商场2018年2月到2019年11月生猪价格数据为依据，用db4小波对原始数据进行去噪处理后，综合EGARCH和NARX模型对短期内生猪价格进行了预测， 得出短期内生猪价格走势。通过对比分析NARX模型和EGARCH-NARX模型的价格走势，研究发现EGARCH-NARX复合模型的预测精度更高，可靠度更强。

关键词：小波分析;时间序列;NARX模型;EGARCH模型

1引言

从2017年各类畜产品占比来看，猪肉已经成为是我国主要的畜牧加工产品，占比达到了62. 48%。生猪价格长期受到社会各界的关注[1]，受非洲猪瘟的影响，近几个月生猪价格波动很大，因此研究不确定因素下对生猪价格的影响，建立相应的预测模型，就显得尤为重要。

生猪养殖紧密联系着乐山地区农户的生产生活，生猪价格的周期性频繁大幅度波动经常导致生猪养殖及相关环节经营困难。生猪价格的大幅波动，首当其冲的是对养殖户的经营造成冲击，使得养殖户难以对接下来的市场价格作出准确预估，往往会造成高成本低回报的局面。探寻生猪价格波动的情况，准确把握未来生猪市场养殖户更加重要。

本文在传统的价格预测模型上，基于小波理论并综合NARX和EGARCH模型，在不确定因素下，对生猪价格进行预测。

2 传统的价格预测模型和波动率模型

首先对传统的价格预测模型和波动率模型进行分析。

2.1传统的价格预测模型及其应用

在农产品的价格预测问题中，现阶段国内外已有很多研究成果，其中较为著名的是小麦价格走势预测，研究发现，卖期货的价格在相当长的一个时期里面处于较高的水平。其他研究学者还发现，白菜价格预测上，最好避免使用ARMA模型。刘海清对农产品价格也进行了预测，得出了芒果在一定时期内的价格走势曲线，并对价格波动进行了深入分析。在过去的预测分析中，虽然对价格走势分析很多，但是对价格的波动却研究得很少。

2.2 波动率模型及其应用

1986年Bolloerselev提出了广义自回归条件异方差模型，即GARCH模型。GARCH（p，q）模型定义为

公式（1）中，ui为残差项，ht为条件异方差，a0>0，ai，为GARCH项系数，bi为GARCH项系数。GARCH模型自产生以来，很多的市场研究专家通过不断的分析和探索，在此模型基础上，进行了改进，使得模型在直观反映价格波动的基础上，还可以反映市场情况，例如MGARCH模型、EGARCH模型等。第二种模型主要应用在金融领域，通过对模型的分析运用，可准确把握基金市场的风险和误差，有效避免基金可能潜在的风险。肖云香、李星野结合数学科学中的多项式算法对我国的外汇储备进行了预测，研究表明，通过模型预测的农产品价格波动，与上市股票的波动性较为吻合。通过分析上海和伦敦期货波动率，学者们对溢出效应、杠杆效应有了进一步的了解。从上面的论述中可以知道，GARCH模型已经被广大学者所认同。

非线性源回归网络是有反馈的动态神经网络，是一种有记忆功能的神经网络，通过当前输入和过去输出这两个方面，来决定当前输出的情况。NARX模型不仅继承了传统的时间序列模型的优点，而且通过训练使得模型对非线性数据有着更好的适应能力，因此，NARX模型非常适合复杂的、非平稳、非线性时间序列的预测。

参数d，m分别是延迟阶数和神经元的个数，可以通过调整d，m的值，来优化模型的预测性能。

由以上分析可知，结合NARAXM模型和EAMD模型对生猪价格进行预测，可以较好的综合各方有因素，对价格波动做出精准预测，有效避免了以往价格预测过程中出现的片面性问题。

3 基于小波理论和EGARCH- NARX的组合模型

小波函数是在传统傅里叶函数上发展而来的，小波变换是通过平移和伸缩等运算对信号进行多尺度细化分析[10]，利用多分辨率分析来得到更多的信息。当满足如下完全重条件则称为基小波。

小波本身具有多分辨分析和良好的非线性局部逼近功能等多种特性，能够对研究对象进行更为细致的逼近，因此小波分析又被人们称为“数学显微镜”[11]。近年來逐渐被引入经济领域，并得到广泛的应用。

基于小波理论综合上述模型，本文提出预测生猪价格的模型结构由以下步骤完成：

Stepl利用小波分析理论对原始数据进行了分析，筛选有效的数据和层数。

Step2对选取的主要趋势数据运用NARX模型进行拟合，并对未来价格进行第一次预测;

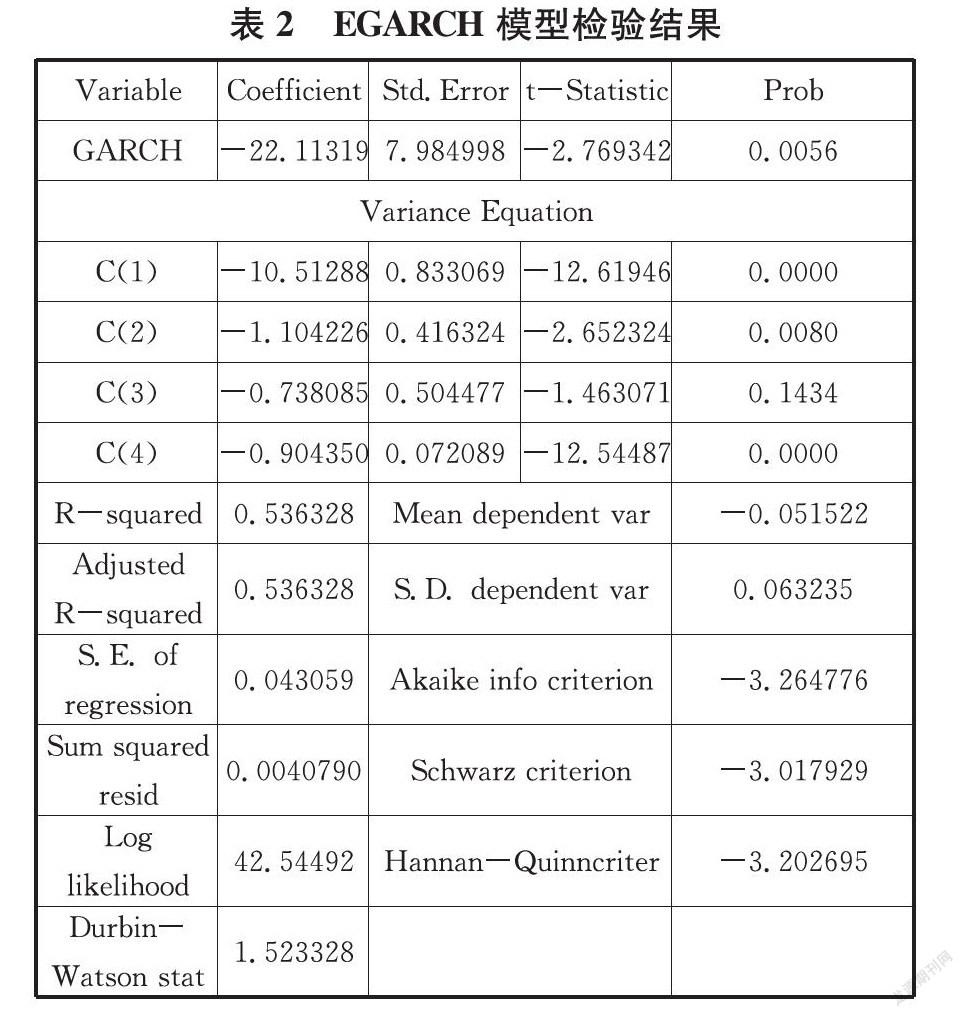
Step3对残差部分进行高阶ARCH检验，若存在高阶ARCH效应则进一步建立GARCH模型并进行第二次预测，反之在第二步处结束。

详见图2[12]。

3.1数据来源

本文选用的模型是短期预测模型，由于生猪价格受政策因素影响比较明显，所以为了提高预测精度，选用的数据是在统一政策时期的数据[13-15]。本文以乐山市市中区华联商场2018年2月到2019年11月的生猪价格为研究对象，数据见图3，用小波对数据分解，经尝试，第一层可以代表原始数据的大部分信息，所以选取第一层的主要趋势进行建模。

3.2平稳性检验

从上图可以看出数据具有明显的上升趋势，初步判断序列不平稳。对数据进行ADF检验，数据不平稳，对数据进行平稳化处理，数据进行一次差分后变得平稳。由ADF检验结果可知，-5. 639824小于1%、5%、10%显著性水平下的临界值，p值趋近于0，根据ADF检验原理序列是平稳的，因此ADF检验通过，即数据经过一阶差分后变平稳。

3.3模型参数估计及模型定阶

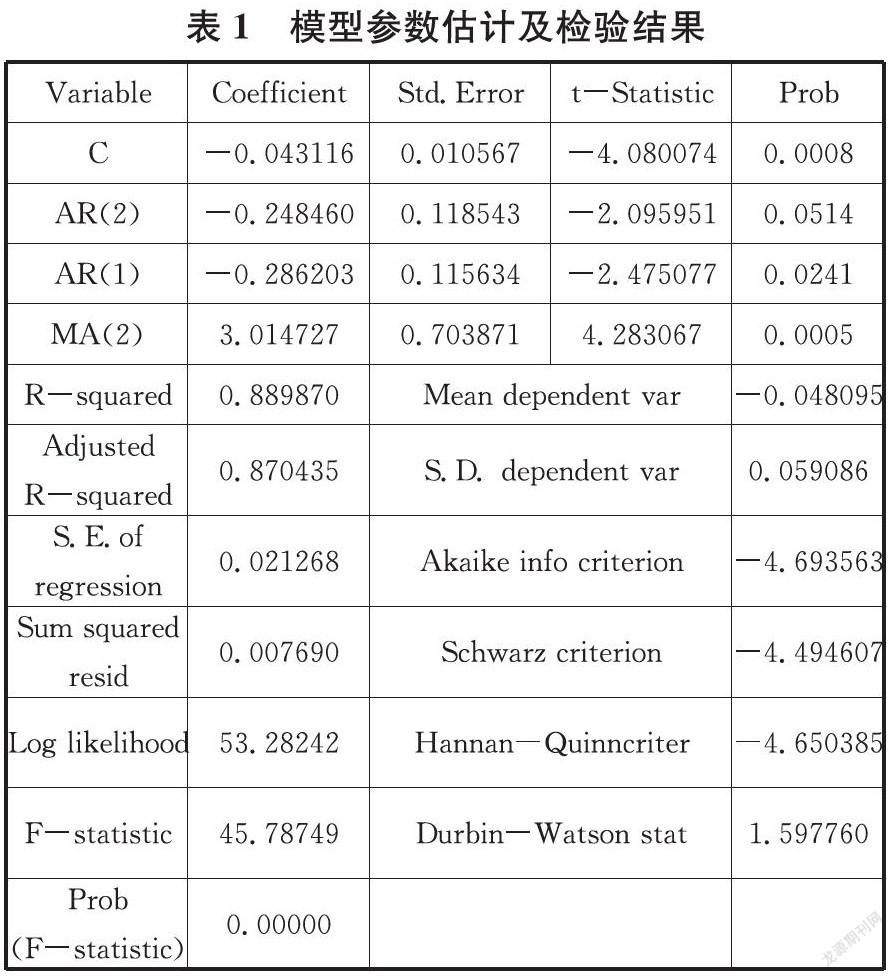
利用自相关与偏自相关函数和Q统计量来检验序列相关性，序列自相关和偏自相关系数、Q统计量对应的p值趋近于0、进行差分后的序列的自相关系数和偏自相关系数如表1所示。

由表1可知，p可以选择1或者2，q可以选择1或者2，由于一阶差分，所以d一1，从而得到NARX （1，1，1）、NARX（1，2，1）、NARX （2，1，1）、NARX（2，2，1）。通过尝试对比四个模型调整后的可抉系数，同时考虑AIC最小准则，最终NARX（2，2，1）模型比较好。模型参数估计及检验结果见表1。

3.4模型检验

通过上面的分析结果可以知道NARX（2，2，1）是最理想的预测模型，从表中的参数可以直观的看出，预测模型的准确度尽可能的提升，对数据的残差部分进行了进一步的校验和检测，从而得出残差部分具有高阶ARCH效应的结论，从而进一步提升了预测模型的精确度。

3.5 预测结果与分析

运用小波预测理论分析对比NARXEGARCH数据，研究发现，运用单一的NARX模型数据误差较大，而NARX-EGARCH模型对于函数的标准误差可以控制在0.4的范围之内，模型的准确度有了很大提升。

4 结论和政策建议

本文通过多个模型对农产品的价格进项了预测分析，并对目前国内热点的生猪价格问题进行了重点分析和预测。通过比较不同模型预测结果的准确度，得出以下结论，基于小波理论的NARXEGARCH模型所得到的数据最为精确，可以在实际的运用过程中根据产品的实际价格变动情况，对更多的产品和领域进行有效的预测。在政策长期稳定的情况下，生猪产品的价格在一定时间内会有所下降，但是下降的幅度不会很高。

虽然我国生猪产量巨大，但养殖行业规模小，有实力的大企业少，产业化经营水平低，标准化养殖系统依然不完善，加强规模化、集约化养殖不仅可以得到更多的市场信息，抵御市场风险的能力也更强，会避免因供需失衡而引起的猪肉价格异常波动，而且也更有利于生猪疫情的防控。

同时，政府应该采取措施加大生猪市场流通，创建良性的竞争环境，建立健全对城镇居民特别是城镇中低收入群体的扶持政策，如可以建立一种物价指数与生活补贴的联动机制，通过分析物价指数涨幅的变化，有条理、有规定地对特定城镇居民在一定时间段内给予一定比例的现金补贴;完善疫病防疫体系，减少疫病对生猪生产的冲击等，通过建立一系列猪肉生产和供给的长效保障机制，保持猪肉价格的基本稳定，尽可能降低猪肉价格波动给城镇居民带来的长期损失。

论文由西南民族大学研究生创新型科研项目资助，项目编号CX2020SP70。

参考文献

[1]阮冬燕，陈玉萍，周晶，中国农户生猪散养动态演化规律分析[J].农业展望，2018（6）：53-58.

[2]王勇，张浩，小麦期货价格预测的马尔可夫模型[J].安徽农业科学，2008.36（5）：17-21.

[3]刘峰，王儒敬，李传席.ARMA模型在农产品价格预中的应用[Jl.计算机工程与应用，2009，45（25）：238- 248.

[4]程贤禄，北京市农产品批发市场蔬菜价格预测预报体系研究[J].北京农业科学，2002（2）：1-10.

[5]刘海清，方佳，基于指数平滑模型的海南省芒果价格预测[J].热带东业科学，2010，30（1）：79-81

[6]杨夫立，基于GARCH模型的证券投资基金VaR计算与实证研究[J].经济问题，2012（6）：87- 91.

[7]肖云湘，李星野，基于小波的回归 GARCH模型及其在外汇储备中的应用[J].上海理工大學学报，2015，37（1）：18-22.

[8]夏冰，农产品价格波动聚集特征验证及趋势预[Jl.经济实证，2015（II）：145-148.

[9]万蔚，江孝感，我国沪、深股市的波动性研究基GARCH族模型[J].价值工程，2007（10）：14- 18.

[10]高辉，赵进文，期货价格收益率与波动性的实证研究 以中国上海与英国伦敦为例[J].财经问题研究，2007（2）：54-65.

[11]陈升，李星野，基于小波分解自回归模型的CPI预测[J]，统计与决策，2012（1）：18-20.

[12]侯光普，乔泽群，基于小波分析和ARMA模型的房价预测研究[J].统计与决策，2014（15）：20- 23.

[13]吴正杰，高温高湿对生猪的危害及应对策略[Jl.中国猪业，2016（6）：23-26.

[14]李志萌，杨志诚，生猪价格波动规律的形成机理与调控对策[J].农林经济管理学报，2016 （6）：694-701

[15]孙秀玲，中国生猪价格波动机理研究[D].北京：中国农业大学，2015.