数字信号处理中窗函数的分析与应用
盛旭然 向前
摘要:数字信号处理技术在当今信息技术高速发展的情况下得到了广泛的应用和发展,在通信领域、工业领域、电子信息领域以及图像处理领域等发挥着重要作用.其中时频变换分析在数字信号处理中的应用非常重要,为了保证信号的完整性,往往在时频变换时需要引入窗函数.对此,文章对数字信号处理中的窗函数问题进行了简要地探讨和研究,对常见窗函数的性能做了分析和对比,使我们可以更好地利用窗函数进行信息处理.
关键词:数字信号;处理技术;时频变换;频谱泄露;窗函数
中图分类号:TN911.72 文献标识码:A 文章编号:1673-260X(2019)05-0074-03
1 引言
我们在数字信号处理时,一般需要限制数字信号的观察时间,即需要选择一段时间的数字信号作为样本,并对其进行分析,得到数字信号处理结果.在数字信号处理过程中,我们所采用的有限个点的数据样本取得过程就是一个将数字信号数据截断的过程,其结果等效于对信号进行加窗函数操作,但相较于加窗函数操作会导致的频谱泄露,数字信号数据截断效果更佳.根据实验可知,加窗函数操作的数据样本中完整的频率数量越多,越容易得到信噪比好的频谱信号.除此之外,采样点数量的增多也会导致后续进行傅里叶变换的运算量增大,降低运算效率.结合实际分析,合适的窗函数能有效地降低频谱泄露等问题.
2 加窗原理分析
根据奈奎斯特采样定律可知,在数字信号转换过程中,当采样信号频率大于样本中信号最高频率的两倍时,采样后的数字信号完整保留了原始信号信息.当采样频率高于信号最高频率的两倍时称之为过采样.通常在实际应用中,采样频率至少是5~10倍[1].过采样的同时还需要尽可能保证得到更多个周期的成分,这就加大了运算量,所以不能取无限长的数据点.
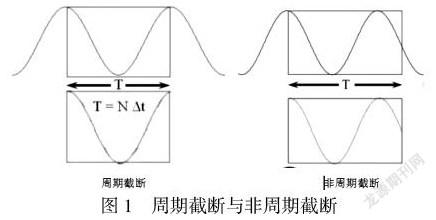
傅里叶变换是数字信号处理的主要数学工具,是用来研究时间域和频率域之间关系的重要工具.在用计算机实现信号处理领域中,对无限长的信号进行测量和运算是不现实的,取其有限的时间序列是常见分析方法,截取有限时间序列的过程叫作信号截断.信号截断分为周期截断和非周期截断.若截断后的信号为周期信号则为周期截断,若截断后的信号不再是周期信号则为非周期截断,绝大部分截断为非周期截断.以一个正弦波为例,如图1所示,然后经过信号截断处理的片段进行周期延拓处理,可以得到一段虚拟的、无限长的信号,针对这段虚拟信号可以进行傅里叶变换等分析处理.
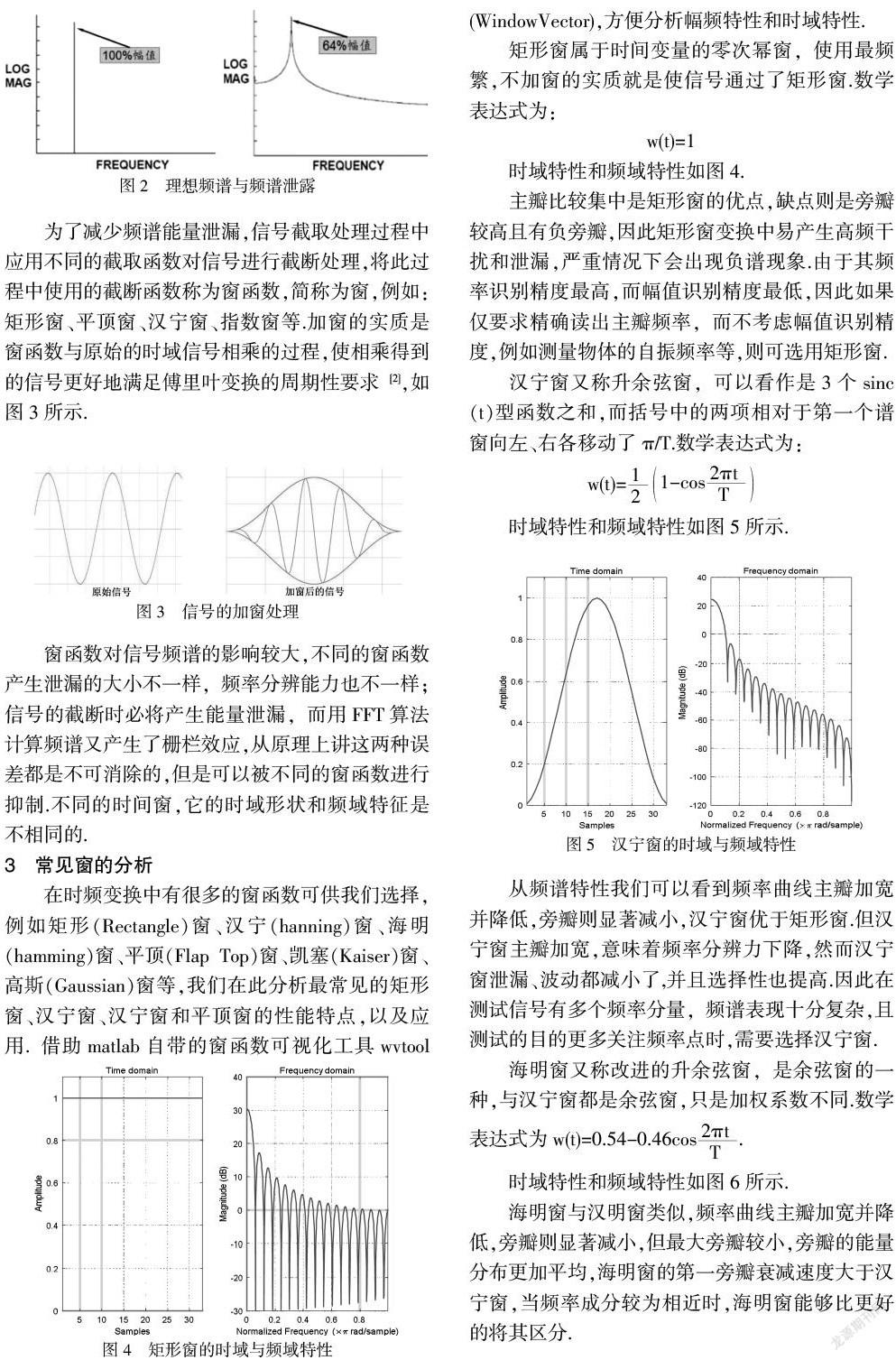
周期延拓的时候会出现一个问题,如果原始信号是一个周期信号,我们得到的频谱应该是一个固定频率的点,但非周期截断后,信号不再是一个周期信号,引入了不可预测的其他频率成分,频谱在整个频带内产生了拖尾现象,频谱发生了畸变,之前集中在一个频率的能量被分散到两个较宽的频带中去了,也就是我们所说的频率泄漏,是数字信号处理过程中非常常见的误差.如图2所示.
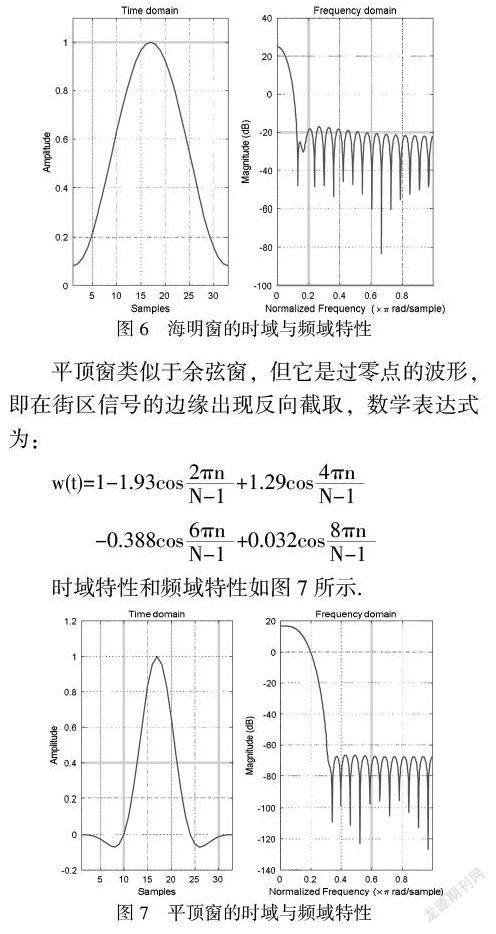
为了减少频谱能量泄漏,信号截取处理过程中应用不同的截取函数对信号进行截断处理,将此过程中使用的截断函数称为窗函数,简称为窗,例如:矩形窗、平顶窗、汉宁窗、指数窗等.加窗的实质是窗函数与原始的时域信号相乘的过程,使相乘得到的信号更好地满足傅里叶变换的周期性要求[2],如图3所示.
窗函数对信号频谱的影响较大,不同的窗函数产生泄漏的大小不一样,频率分辨能力也不一样;信号的截断时必将产生能量泄漏,而用FFT算法计算频谱又产生了栅栏效应,从原理上讲这两种误差都是不可消除的,但是可以被不同的窗函数进行抑制.不同的时间窗,它的时域形状和频域特征是不相同的.
3 常见窗的分析
在时频变换中有很多的窗函数可供我们选择,例如矩形(Rectangle)窗、汉宁(hanning)窗、海明(hamming)窗、平顶(Flap Top)窗、凯塞(Kaiser)窗、高斯(Gaussian)窗等,我们在此分析最常见的矩形窗、汉宁窗、汉宁窗和平顶窗的性能特点,以及应用.借助matlab自带的窗函数可视化工具wvtool(WindowVector),方便分析幅频特性和时域特性.
4 窗函数的选择与应用
单从窗的频谱他特性上看窗的波形图显示了窗本身为一个连续的频谱,有一个主瓣,若干旁瓣.旁瓣的高度显示了加窗函数对于主瓣周围频率的影响.对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应.通常低旁瓣会减少傅里叶变换的频谱泄漏,但是会增加主瓣的带宽.旁瓣的跌落速率是旁瓣峰值的渐进衰减速率.增加旁瓣的跌落速率,也可减少频谱泄漏.所以窗函数频谱的主瓣越窄越好,即能量尽可能集中在主瓣内,以提高谱估计时的频域分辨率和减小泄漏[4].
选择加窗函数并非易事.每种加窗函数都有其特征和适用范围.要选择加窗函数,必须先估计信号的频率成分.
如果信号中干扰频率分量较强,与感兴趣频率分量相距较远,那么就应选择具有高旁瓣下降率的平滑窗.如果强干扰频率分量与感兴趣分量相距较近,那么就應选择具有低最大旁瓣的窗.如果感兴趣频率包含两种或多种很距离很近的信号,这时我们最好选用具有窄主瓣的平滑窗.如果一个频率成分的幅值精度比信号成分在某个频率区间内的位置更重要,选择主瓣能量集中的窗,如平顶窗.如信号频谱较平或频率成分较宽可以不使用窗[5].
5 总结
窗函数在信号处理中有着非常重要的地位,它保证了信息的完整性和准确性,选择适当的窗函数就显得尤为重要.文章通过对具体窗函数的分析比较,说明了窗函数在实际信号处理中的实现,在对不同窗函数进行比较的过程中总结窗函数如何选择与应用.现代工程中加窗的应用已经十分成熟,但随着技术的进步和需求的改变,会出现更多针对具体应用场景的窗函数.
参考文献:
〔1〕薛年喜.MATLAB在数字信号处理中的应用[M].北京:清华大学出版社,2008.153—163.
〔2〕李杭生,陈丹.频谱分析中窗函数的研究[J].微计算机信息,2008,24(10):278-279.
〔3〕田园,周勖.窗函数在数字滤波器设计中的应用[J].国外电子测量技术,2013,32(4):25-27.
〔4〕杨丽娟,张白桦,叶旭桢.快速傅里叶变换FFT及其应用[J].光电工程,2004,31(b12):1-3.
〔5〕尤会恩,刘建军,张文.数字信号处理中窗函数类型及选择原则[C]//全国敏感元件与传感器学术会议,2005.
〔6〕郑星亮,程洁,魏任之.数字信号处理中的窗效应及窗函数的应用原则[J].北京联合大学学报,1997(2):34-37.
〔7〕类淑趁,耿麦香,许建宾.论数字信号处理中加窗的影响及窗函数的选择原则[J].山西矿业学院学报,1995(4):347-350.

