基于学业质量评价的两市特优生数学能力差异分析

罗媛

本文以四川省内AB两市特优生为评价对象，用同一套试卷作为评价工具，对评价数据进行分类统计分析，得到两市特优生数学能力的特征差异，通过访谈与归因得到教学改进调整的建议。

选取AB两市的特优生，按统一命题、统一标准进行测试，对试题进行得分统计分析，以此为依据，对后期教学计划和课程内容做出适当调整。

一、评价工具及样本对象

（一）工具性质

使用《某市2016级高三一诊考试理科数学试卷》作为监测工具，测试对象整体为15522人，实测信度0.85、效度0.51、区分度超过0.3的题目占全卷92%，工具整体基本可靠。

（二）样本对象

样本来自A、B;两市，以下A市代表省会城市名校的平行班学生，B市1类为省内某二级城市的私立校学生、B市2类为该二级城市国家级示范校学生。将三类样本在相同的时间和条件下，用同一套工具完成测试、同一标准给予评分。

二、测验结果及数据分析

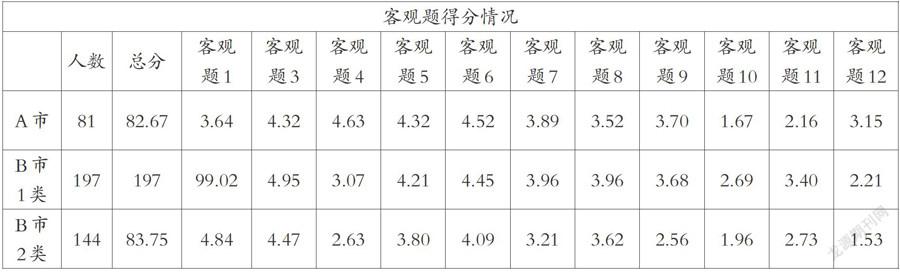
（一）客观题得分情况

B市1类校总分远高于A市，A市与B市2类学生总分基本接近。

A市学生在客观题1、3、10、11上有明显劣势，对应的考察内容为：1集合的运算、3简易逻辑、10三角函数及其性质、11数列中an与Sn关系;考察难度都属于了解和知道范畴，试题难度不高。

B市2类学生在客观题4、5、6、12上有明显劣势，对应的考察内容为4统计图表，直观想象均值、方差大小、5函数图象识别、6二项式定理指定项、7向量几何形式的线性运算与数量积。B市1类学生在客观题12即函数与不等式版块上得分率低于A市学生。

（二）主观题得分分析

在总分最低的情况下，A市在主观题14、21上有明显优势，对应考察的知识内容有：14向量的坐标运算、21导数与切线方程，极值点，不等式，含参讨论。但在19k方检验，古典概型上呈现出明显弱势。

B市2类学生在14向量的坐标运算、15三角值的计算、16函数与导数等内容得分率低。

三、特征分析及措施建议

针对以上数据现状，在A、B两市各选择2～4位授课教师和部分学生进行访谈，结论如下：

（一）基本知识和基本概念掌握不清

本次选择的A、B两市学生均是在当地市州学业成绩位于前百分之一的特优生，但AB市的学生均呈现出特优生在基础知识和基本能力上掌握不牢的情况，出现集合、简易逻辑、向量、三角函数等知识版块的基础问题上得分率较低。证明特优生在简单问题上丢分的情况依然普遍存在。

自我归因的过程中，学生认为问题的核心差错出现在：概念不清晰以及审题不清晰。进一步向前归因，特优生在日常学习中会出现以参考资料为纲，忽视课本、忽略基本概念辨析的情况;在课后训练中，对常规知识训练也较为忽视，对日常的中低难度题目错误认为是偶尔错误，较少深入归因，此类错误成为特优生自我反思的漏网之鱼。

（二）课程重心及教学内容设计差异

评价结果看出，A市学生在高阶思维能力上呈现较好的发展，体现在14向量、21导数与切线方程，极值点，不等式，含参讨论等需要抽象、推理、多次转化的难题上，较多学生呈现出较好的掌握结果，师生均认为这一结果与其日常教学中的常规教学和训练有直接关系，学生认为这类题目比较常见、比较有趣。

B市2类学生的教学课程安排上，重点多次重复向量坐标、三角函数、函数与导数等章结的基本知识和基本内容，但B市2类学生在这部分题目的得分率不高。

A、B两市教师进行比对探讨认为：在某一点知识体系和问题上进行多次重复的讲解，只会造成学生的疲惫和漠视，难以帮助学生突破困难和形成能力。建议将教学内容进行适度提高难度，加强思维训练的难度、灵活性和抽象性以后，反而会有利于吸引学生兴趣、有利于达成该版块的知识目标。相应的，B市2类的学生对14、21等题目较多呈现出陌生、畏惧的状态。

B市1类校学生在整个测试中取得了较好的成绩，但依然出现了12、21题低于A市学生的情况，教师在课程安排中课程比较全面，但学生普遍学习时间更长。

（三）关注学生的成就动机和自我效能感差异

在學生访谈过程中，A市学生呈现出更高的自我效能感，对很多问题会强调“我能行，偶尔错，下次没问题”。而作为得分更高的特优生，B市学生对未来的评估更加谨慎，在成就动机上体现出更多“避免失败”的特点，B市教师在日常训练题目的选择上更加谨慎和保守。

学生在不同市域、不同学校学习，受到学校文化、课程内容、教学设计和教师等多方因素的影响，在后续教学过程中，可考虑更多地进行异市之间相同学生对象和教学过程的数据对比分析，帮助教师扩大视野、取长补短、及时调整。

（责任编辑  袁 霜）