基于Dogit模型的离散劳动供给行为估计

张晨 万相昱

摘要：由于离散劳动供给模型在非劳动参与、随机偏好、复杂税收等问题的处理上具有较强的灵活性和适用性，故而近年来被愈来愈多地应用于微观个体劳动供给行为的研究中。劳动力市场中的“不妥协”性和劳动供给选择之间的相关性仍然是传统离散模型无法解决的难题。以2013年中国家庭收入调查数据（CHIP2013）作为研究样本，通过建立Dogit模型来处理传统离散模型的“无关选项独立”性和刻画劳动力市场上普遍存在的“不妥协”性，进而对城镇居民劳动供给行为进行估计。实证结果表明，劳动供给者对某些选择具有显著偏好，即劳动力市场的“不妥协”性显著存在，同时，与传统离散模型相比，Dogit模型预测非劳动参与的准确性更高。

关键词：离散劳动供给模型;多项Logit模型;Dogit模型;“不妥协”性;劳动供给选择：非劳动参与

中图分类号：P467 文献标识码：A 文章分类号：1674-7089（2019）06-0065-15

作者简介：张晨，中国社会科学院大学（研究生院）博士研究生;万相昱，博士，中国社会科学院数量经济与技术经济研究所副研究员。

一、引言

微观个体的劳动供给行为是指个体关于收入与闲暇的权衡而非劳动供给总量，国际上通常采用结构模型对其进行估计（尽管国内相关研究较多，但一般采用Heekman两步法或者Tobit等非结构连续模型）。根据模型中劳动时间或者闲暇的连续性，结构模型可以分为离散劳动供给模型和连续劳动供给模型。传统连续劳动供给模型将劳动时间或者闲暇作为一个连续和无约束变量处理。其中，Hausman等学者较早开始了税收影响劳动供给的估计研究，首次给出了连续劳动供给模型的估计方法。其基本思路是：利用数值模拟，从效用函数和预算约束中求得个人或者家庭的最优劳动供给时间，如果预算约束是线性的，那么将得到能够使直接效用水平最大化的劳动时间，但是税收的存在可能会导致非线性预算约束.所以需要知道直接效用函数，进而以直接效用最大化作为目标求得劳动供给时间。研究步骤如下：首先，将关于税收问题的非线性约束前沿视为一些凹子集，使每一个凹子集局部最大化;其次，给出不需要计算直接效用函数就可以得到最优劳动时间的搜索方法;最后，将真实劳动时间和最优劳动时间之间的误差设定为截断二元正态分布，采用极大似然方法对参数进行估计。该研究为后续研究利用连续劳动供给模型估计劳动供给行为提供了如下建模思路和步骤：第一步，利用效用函数求解最优劳动供给时间，主要采用数值模拟方法;第二步，设定最优劳动供给时间和实际工作时间之间误差的概率分布类型;第三步，构造似然函数进行极大似然估计。国外主流学者均采用类似的思路对劳动供给进行估计，目前国内学者尚未采用此类方法进行微观个体劳动供给行为的建模和估计。

由于连续劳动供给模型在处理最优化和税收等问题时存在诸多不便，离散劳动供给模型逐渐受到关注，其中，Soest较早基于多项Eogit模型对劳动供给行为进行估计，提出了离散劳动供给模型的一般性框架。此类模型将劳动供给时间视为离散变量的做法与实际更相符，并且在处理异质性偏好、非劳动参与和政策模拟等方面具有较高的灵活性，因此，近年来离散劳动供给模型的应用越来越广泛，特别是在微观模拟方面。

实际上，连续劳动供给模型与离散劳动供给模型各有优劣。连续劳动供给模型的最大优点在于完全根据劳动经济理论构建，即在预算约束条件下，求解能够使个人效用最大化的最优劳动供给时间。但是，在实证研究中实现求解最优劳动供给时间这一目标通常存在较大挑战，具体体现在如下三个方面。首先，在利用预算约束和效用函数求解最优劳动供给时间的过程中，由于税收和福利政策的复杂性，甚至可能不存在合适的税收和福利函数，通常无法确保满足预算约束集合的凹性假设，所以寻找最优解较为复杂。其次，在构造似然函数时需要单独刻画非劳动参与样本，特别是在估计夫妻联合劳动供给时，需要考虑多种复杂情况。最后，由于似然函数具有非闭合形式（Non-closed form），所以在引人异质性偏好或者随机偏好时往往需要涉及多重积分，这会使计算复杂程度大幅度提高。

与连续劳动供给模型相比，离散劳动供给模型具有四个方面的优点。首先，不必考虑最优解的存在性。离散劳动供给模型将劳动时间设定为若干个离散点，相应的预算约束为一系列点的集合，只需直接进行点与点的比较，不涉及判断最优解的存在性问题。其次，易于处理复杂的税收和福利政策。由于现实中的税收和福利机制较为复杂，因此采用函数进行刻画较为困难，对于连续劳动供给模型而言，必须要寻找合适的函数来表示税收和福利，却不能确保满足预算约束集合的凹性假设。而离散劳动供给模型只需计算最终得到的税收和福利数值，不涉及税收和福利函数、凹性假设。再次，离散模型可以直接处理非劳动参与问题。可以将非劳动参与直接设定为一个劳动供给选择，而无需像连续模型那样单独考虑非劳动参与的分布。最后，由于离散劳动供给概率具有闭合特征，所以计算更加简单。特别是引人工资率误差、异质性偏好之后，可以采用模拟方法解决多重积分问题。正是由于离散劳动供给模型的上述优点，所以国外学者普遍采用离散模型研究劳动供给问题。反观国内，目前采用上述离散模型估计劳动供给的研究才刚刚起步，仅万相昱、张世伟、李雅楠等学者的三篇文章涉及。

尽管离散劳动供给模型具有诸多优点，但是由于这类模型假设劳动供给时间的选择概率为Eogit类型，在本质上属于由Mcfadden于1977年提出的多项Logit模型，所以它通常难以处理如下两个问题。第一，多项Logit模型要求误差分布类型为极值分布，且满足独立同分布假定.由此衍生出众所周知的“无关选项独立”性问题.也就是要求选择之间具有无关性，这与实际并不相符。第二，个体对于某些选择具有较强的偏好，难以发生变动，也就是由Harris和Duncan两位学者提出的劳动力市场中的“不妥协”性问题。

由于传统离散劳动供给模型无法处理上述“无关选项独立”性问题和“不妥协”性问题，所以相关的拓展研究主要围绕如何处理这两个问题展开。Gaudry等学者提出了一种改进的离散选择模型（Dogit模型），能够在一定程度上解决上述问题。该模型假设个体对某个选项的选择来源于两部分，通过设定特定的偏好参数和选择偏好概率使其可以在一定程度上刻画“不妥协”性，并且有效避免“无关选项独立”性问题。因此，相较于一般的Logit模型，Dogit模型更加符合现实，且具有如下四个优点。第一，模型设定并不满足“无关选项独立”性，不会明显违背现实;第二，将Eogit模型嵌套在内，易于进行假设检验;第三，概率具有闭合表达式，易于计算;第四，专门设置参数用来刻画决策者对于某些选择的偏好或者“不妥协”性。尽管如此，Dogit模型也存在不足。比如，由于Dogit模型在个体偏好设定时未考虑個体异质性问题，进而导致用于度量偏好或者“不妥协”性的参数对于所有个体均相同，这显然与现实并不完全吻合。

但是Dogit模型还是由于诸多优点而受到众多学者的关注。比如，Harris和Duncan利用Dogit模型研究了劳动力市场中的“不妥协”性，Fry和Harris开发了有序Dogit模型并将其应用于通货膨胀预期的研究之中，Qi和Dou应用Dogit模型对出行方式选择进行了预测。刘好德、田丽君等国内学者各自运用Dogit模型研究了交通出行方式的选择问题。然而，目前尚未发现有学者应用该模型研究和分析国内经济问题。

综上所述，连续劳动供给模型在求解最优劳动供给时间时面临复杂性挑战，传统离散劳动供给模型（即Eogit模型）难以处理“无关选项独立”性和劳动力市场中“不妥协”性问题，而Dogit模型作为Logit模型的改进模型尚未应用于国内经济问题的研究之中。因此，本文基于Dogit模型对微观个体的劳动供给行为进行了估计，并将估计和预测结果与传统离散劳动供给模型进行对比分析。

后文结构安排如下：第二部分设定离散劳动供给模型，给出基于Dogit模型的离散劳动供给模型的构建步骤;第三部分进行实证分析，具体地，以2013年中国家庭收人调查数据作为样本，分别估计男性和女性的劳动供给，比较传统离散供给模型与基于Dogit的离散供给模型在估计效果和预测准确性方面存在的差异;第四部分为研究结论。

二、基于Dogit模型的劳动供给选择

（一）选择概率

三、实证分析

（一）变量选择

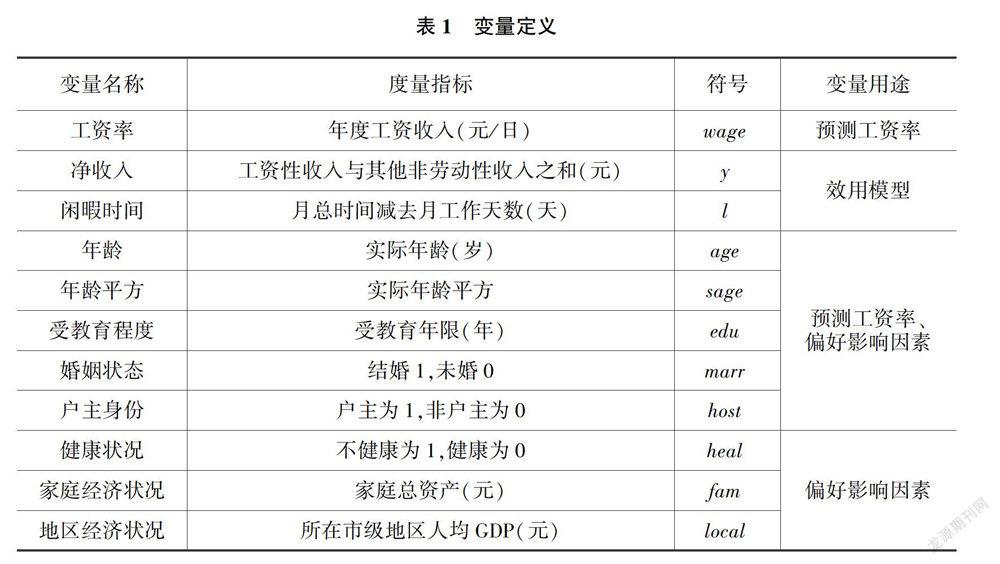
实证模型所涉及的变量及其度量方法如表1所示。模型的核心解释变量为收入和闲暇时间，个人特征、家庭特征和地区特征三类变量作为偏好影响因素用于解释个体偏好差异。

工资率的度量为年工作收入总额（工资性收入或经营净收入的总额，工资性收入包括各种货币补贴）除以年工作时间，其单位为元/日。对于有工作的样本，工资率可以直接计算得到，而对于没有工作的样本，在进行参数估计之前需要基于前文所述的Heckman两步法预测其工资率。净收人为工资性收入（工资率乘以月平均工作天数）加上其他非劳动性收入。工作收人总额、非劳动性收人、年工作时间、工作时间、年龄、受教育年限（不包括跳级和留级年数）、婚姻状況、家庭总资产、户主身份、健康状况、家庭经济状况、地区经济状况等指标可以通过中国家庭收入调查数据（CHIP）的相关问卷得到。需要注意的是，非劳动性收入指问卷中折算成货币的月“伙食补贴”与“住房福利”之和，家庭总资产为问卷中“住户金融资产余额”“动产估价”“经营性资产”三者之和，健康状况为不健康是指问卷中关于健康问题的回答为“不好”和“非常不好”。

年龄、家庭经济状况、地区经济状况在实证过程中均取自然对数。因为可能存在受教育年限为0的样本，所以将受教育年限加1之后再取自然对数。

（二）描述性统计

除特别说明之外，所有原始数据均来自2013年中国家庭收人调查数据（CHIP2013）。该数据来自中国国家统计局2013年城乡一体化常规住户调查样本库，按照东、中、西分层进行系统性抽样.覆盖15个省份126座城市所辖的234个县区.样本规模为18948户家庭，共计64777人。其中，城镇家庭为7175户，农村家庭为11013户，流动人口家庭为760户。这里仅选择城镇样本，具体筛选条件为：第一，年龄在16至60周岁之间的男性和女性样本;第二，剔除学生、退休职工、雇主、自由职业样本;第三，剔除出现主要变量数据缺失和明显填写错误（比如工作时间为0，但是有工资性收入）的样本。最终获得合格男性样本3006人，合格女性样本2379人，样本总规模为5385人。

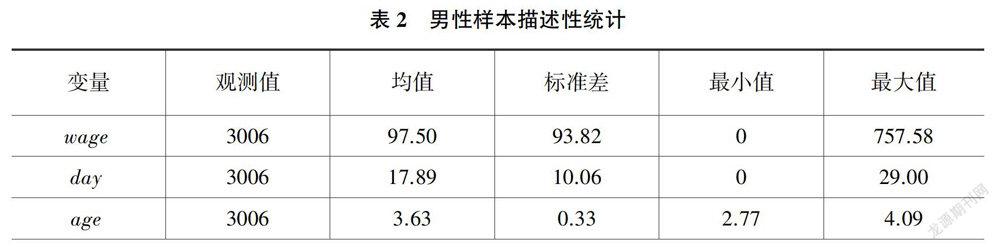
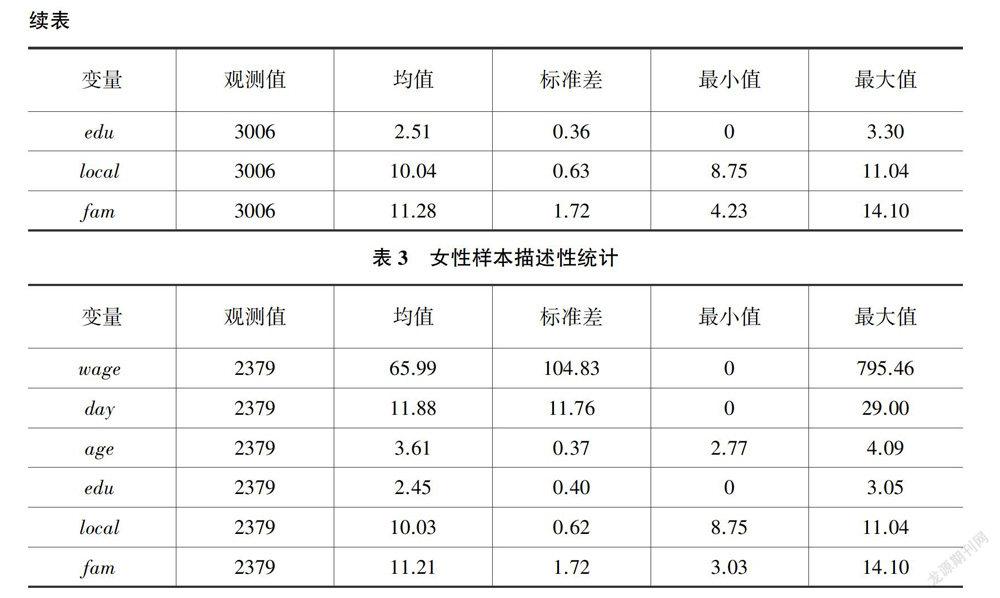
表2和表3分别对男性样本和女性样本进行了描述性统计。直观起见，此处未对工资率（wage）和工作时间（day）取自然对数，其余连续性变量均为取自然对数后的统计结果。男性样本中，无工作个体共有697人，已婚人数为2450人，身份为户主的样本量为1811人，身体状态为不健康的个体有89人。男性的平均日工资为97.503元，月工作天数为17.889。女性样本中无工作的个体共有1163人，明显高于男性，已婚数量为1878人，身份为户主的样本为715人，身体状态为不健康的样本共有76人。

女性样本的工资率和工作时间均明显低于男性，但是男性样本工资率和工作时间的变异系数均明显低于女性，说明女性样本之间工资率和工作时间的差异程度均高于男性样本。

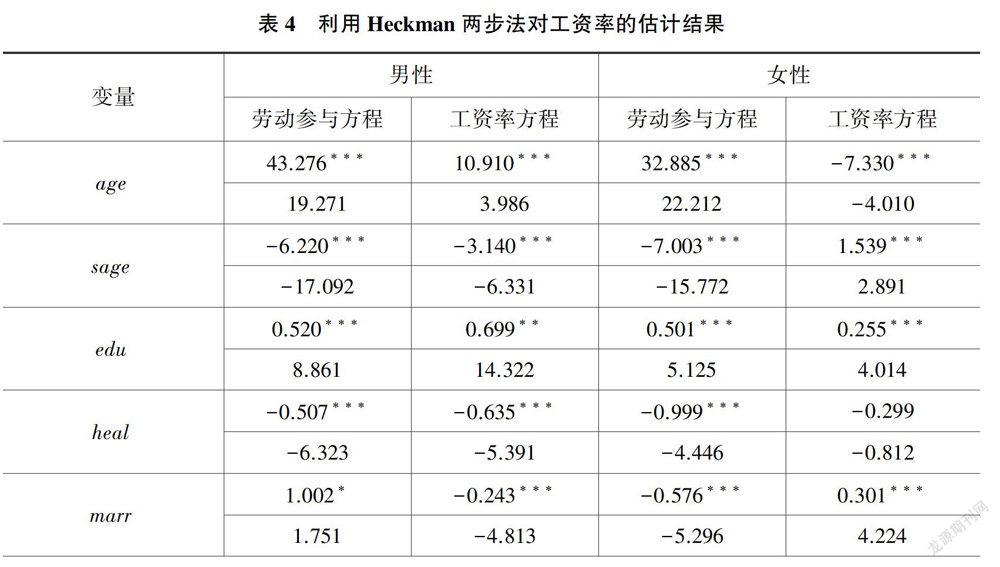
表4为利用Heckman两步法对工资率的估计结果。将男性样本与女性样本的工资率分开估计，并且为了防止遗漏变量带来的估计不一致问题，将工资率方程中的解释变量纳入劳动参与方程之中。表中对lambda的估计结果均显著，说明有必要利用Heckman两步法来解决选择性偏差问题。

（三）买证结果

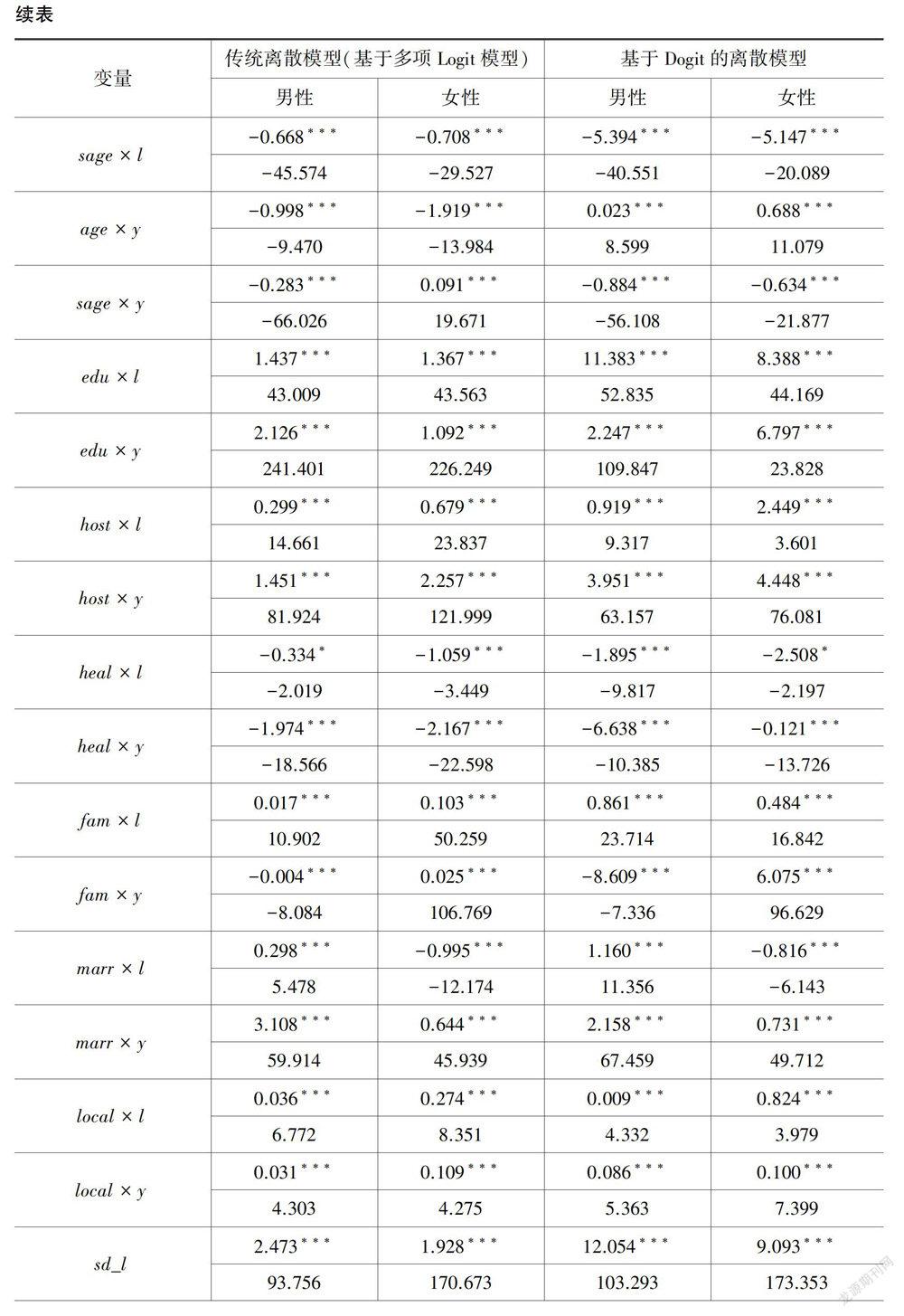
将男性和女性的劳动时间选项分别设定为0、19.60、23.20、27.90与0、19.60、23.10、28.00，总时间为30。表5给出了劳动供给模型的估计结果，参数估计采用模拟极大似然方法，标准差根据得分矩阵的协方差计算得到。第四列和第五列是基于Dogit模型的估计结果。可以看到，效用函数中一次项系数均大于0，二次项的系数均小于0，并且均在1%的显著水平上显著，说明无论男性样本还是女性样本，闲暇时间、净收人与效用水平之间均呈现倒u型关系，并非闲暇时间越多或者净收入越高效用水平就越高。考虑到两者之间的替代性，闲暇时间和净收人的交互项（l×y）系数估计结果分别为-1.930和-9.987，均在1%的显著水平上显著，说明闲暇时间和净收人存在显著的替代关系。

再来分析对于异质性偏好设定的估计结果。从表5的第四列和第五列可知，个体特征与闲暇时间的交互项（age×l、sage×l、edu×l、host×l、heal×l、marr×l）都具有统计显著性。其中，年龄与闲暇时间偏好呈现出显著的倒u型关系，受教育程度、户主身份、婚姻状态与闲暇时间偏好之间交叉项的回归系数均大于0，不健康的身体状态对于闲暇时间偏好具有显著的负向影响。家庭特征和地区特征与闲暇时间的交互项（fam×l、local×l）同样具有显著大于零的估计结果。从显著性水平和影响方向上来看，个体特征、家庭特征和地区特征对于净收人偏好的影响与其对于闲暇时间偏好的影响基本一致。sd_l和sd__y分别表示净收人和闲暇时间的随机偏好项，相应的估计结果表明，对于男性来说，无论是净收人还是闲暇时间偏好均具有显著的随机特征，但是对于女性来说，仅有闲暇时间偏好具有随机性。

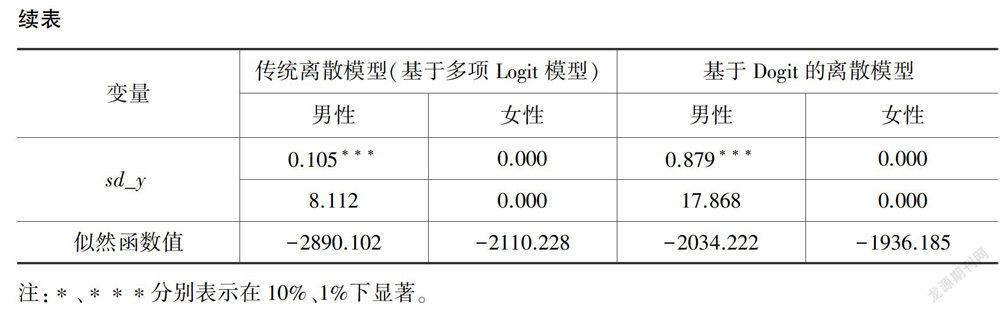
表5的第二列和第三列为传统离散劳动供给模型的估计结果。将其与基于Dogit模型的实证结果（表5的第四列和第五列）相比较，发现二者的各个估计项所对应的估计系数符号和显著性基本一致。前文曾提到，可以将Logit模型作为Dogit模型的一个嵌套模型（θ=0）进行统计检验。计算似然比统计量发现，男性取值为1711.76，女性取值为348.09，均在1%的显著水平上显著。这表明，在离散劳动供给行为的估计中，基于Dogit的离散模型比传统离散模型具有更高的显著性。

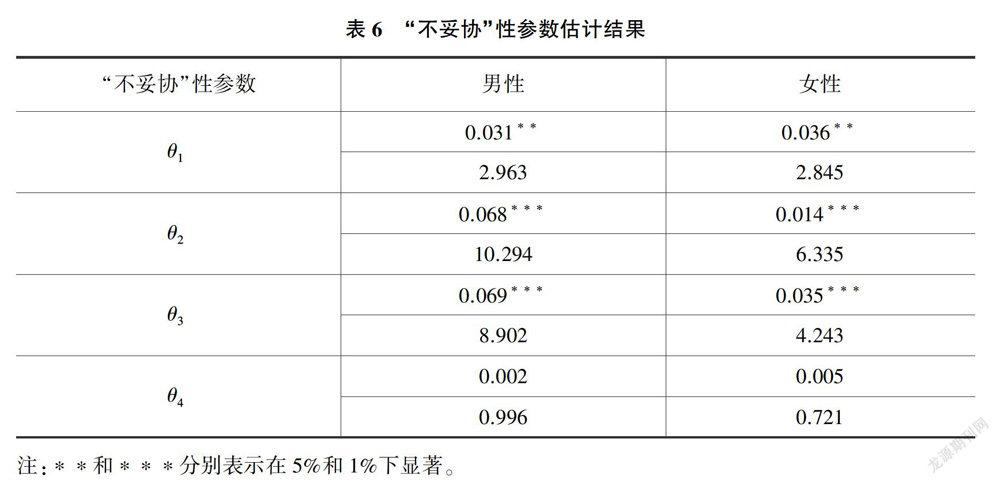
表6为Dogit模型对“不妥协”性参数的估计结果。可以看到，劳动供给者对于不同勞动状态的“不妥协”性具有明显差异。θ1为非劳动参与选择（工作时间为0）的“不妥协”性参数，θ2、θ3、θ4为其他三个工作时间选项（男性依次为19.60、23.20、27.90，女性依次为19.60、23.10、28.00）的“不妥协”性参数。无论对于男性还是女性，θ1、θ2、θ3三个参数均具有统计显著性。男性更倾向于正常的月工作时间（19.60和23.20），但是女性更倾向于选择工作时间为0（不工作）和23.10。参数θ4在统计上不显著，意味着所有人都不愿意较长的劳动时间供给。“不妥协”性参数θ1的显著性说明传统离散模型关于非劳动参与选择概率的估计具有一定的偏差，而Dogit模型在离散劳动供给行为估计中所得到的选择概率更加准确。

（四）预测概率

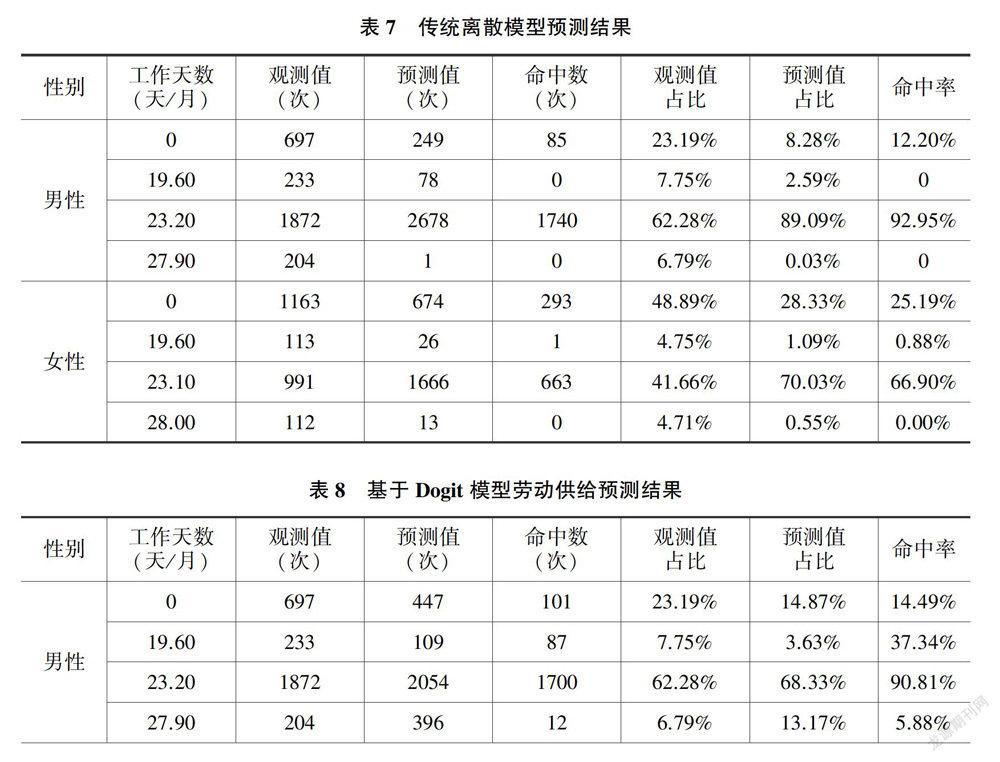
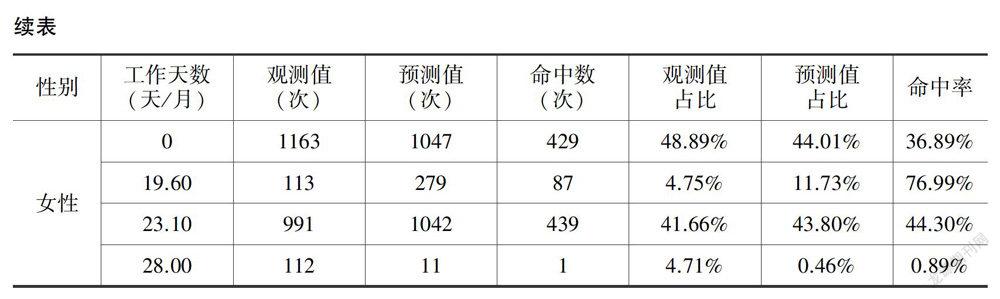
劳动供给模型常用来模拟政策效果，预测的准确率是衡量模型优劣的重要指标。根据原始数据和表5中的估计结果，分别计算个体关于月工作天数（工作时间）的4个选项（男性为0、19.60、23.20、27.90，女性为0、19.60、23.10、28.00）的选择概率，以概率最大的工作天数作为预测值。表7和表8依次为传统离散模型和基于Dogit模型的预测结果。

不难发现，Dogit模型与传统离散模型的预测能力各具优劣。传统离散模型在对观测占比较高的常规劳动时间（男性为23.2，女性为23.1）进行预测时，命中率较高（男性为92.95%，女性为66.90%）。相比之下，Dogit模型对相应项目的预测效果略差（男性为90.81%，女性为44.30%）。但是，在对观测占比较低的劳动时间供给（比如被广泛关注的非劳动参与）进行预测时，Dogit模型的预测效果优于传统离散模型。传统离散模型在预测非劳动参与时的命中率分别为12.20%（男性）、25.19%（女性），而Dogit模型的相应预测结果分别为14.49%（男性）、36.89%（女性）。此外，Dogit模型对于其他两种劳动供给时间的预测效果也更好。

四、结论

本文基于Dogit模型对离散劳动供给行为进行了估计，该模型可以有效避免传统多项Logit模型明显与实际不符的“无关选项独立”性问题，并且通过“不妥协”性参数在一定程度上刻画了劳动力市场上的“不妥协”性。通过对基于Dogit的离散劳动供给模型和传统离散供给模型（基于多项Logit模型）的估计结果进行比较，可以得到两点结论：第一，前者认为个体对于不同选择具有不同的“不妥协”性，即个体会更加偏好于某些选择，从“不妥协”性参数的估计结果来看，劳动供给者确实对于某些劳动时间具有显著偏好。第二，基于Dogit的离散劳动供给模型在对非劳动参与等其他劳动时间的预测上具有优势，而传统离散供给模型对常规劳动时间的预测具有较高的准确性。

国内关于劳动供给行为的实证研究更多地采用非结构模型，极少采用在国外应用广泛的离散劳动供给模型.希望能够通过本文关于两种离散劳动供给模型估计结果的比较分析为国内相关研究提供参考和借鉴。

（责任编辑：来向红）