HPM视角下圆的面积公式教学

王雅琪 瞿鑫婷

【摘 要】“圆的面积”是沪教版数学六年级上册的内容。在已有的教学设计中，大多数教师依照教科书的编排方式，将圆面积转化为已学图形面積进行计算。在这种教学方式下，学生难以真正体会极限思想和“以直代曲”思想。为了让学生更好地体会图形变化中无限逼近的数学思想，更深入地理解圆面积公式，文章从HPM视角对“圆的面积”设计教学，通过融入刘徽的割圆术、阿基米德的同心圆法、开普勒的分割变形法等数学史料，促进学生对圆面积公式的理解，帮助学生突破认识上的障碍。

【关键词】HPM;圆的面积公式;极限思想

“圆的面积”是沪教版数学六年级上册的内容。各版本数学教材分别采用了不同的引入方式：人教版、北师大版、沪教版以生活背景问题引入，苏教版以数方格方法引入，西师大版以圆周长公式引入。各版本数学教材关于圆面积公式的推导均采用割圆拼补法，虽然转化的目标图形不同，但所蕴含的转化思想是一致的。

在已有的教学设计中，大多数教师依照教科书的编排方式，启发学生动手操作，将圆面积转化为已学图形面积[1-7]。受教科书给出的拼图方法（用扇形拼成近似平行四边形）的影响，学生往往认为圆面积公式是一个近似公式，而非准确公式，故难以真正体会极限思想和“以直代曲”思想，也难以接受拼图法在极限的情况下能将圆转化为平行四边形、长方形。这些问题反映出学生对圆面积公式的探究和理解还不够到位。而少数HPM教学设计为了解决以上问题，采用了开普勒等积变换方法。但在教学实践中，有些教师直接将三角形面积代替了扇形面积，没有体现极限的过程[8-9]。

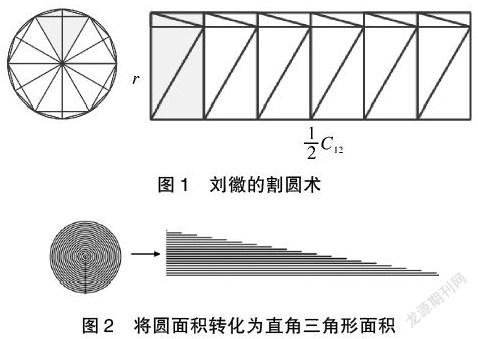
为了让学生更好地体会图形变化中无限逼近的数学思想，更深入地理解圆面积公式，笔者尝试从HPM视角对“圆的面积”进行教学，通过融入刘徽的割圆术、阿基米德的同心圆法、开普勒的分割变形法等数学史料，促进学生对圆面积公式的理解，帮助学生突破认识上的障碍。基于以上考虑，笔者拟定了如下教学目标：

①知道圆面积概念，理解和掌握圆面积的计算公式，并能正确计算圆面积。

②通过剪圆的操作过程，培养学生的直观想象能力、动手操作能力、抽象概括能力和自主探索能力;通过交流与分享圆面积公式的推导过程，提升学生的语言表达能力。

③探索圆面积公式，体会“以直代曲”“圆出于方”的转化思想和极限思想。

④了解历史上数学家推导圆面积公式的方法，理解数学文化的多元性，体会数学背后的人文精神，感悟数学的应用价值。

1刘徽与圆面积公式

公元263年，刘徽在为《九章算术》作注时用割圆术证明了圆面积公式。所谓割圆术，是用圆内接正多边形面积无限逼近圆面积的方法。刘徽在注中称：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣。”如图1所示，刘徽在单位圆内作出内接正十二边形，利用出入相补原理，将正十二边形拼成一个长为正十二边形的半周长、宽为圆半径的长方形[10]。再作圆内接正二十四边形、正四十八边形、正九十六边形……相应得到与多边形等面积的长方形。圆被分割得越细，长方形面积就越接近圆面积。随着正多边形的边数越来越多，相应长方形的长就越来越接近圆周长的一半，而宽始终等于圆半径。最后通过长方形面积公式得到圆面积公式——半周长乘半径。

2阿基米德与圆面积公式

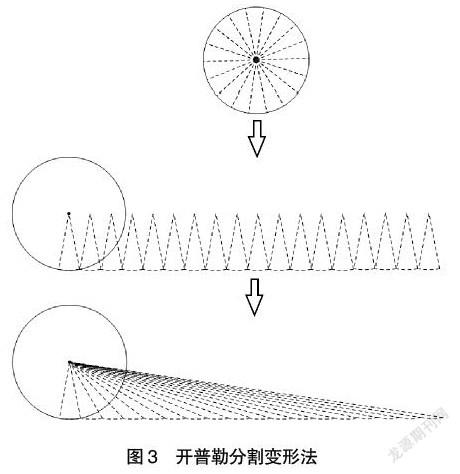
公元前3世纪，古希腊数学家阿基米德在《圆的度量》一书中给出一个命题：“圆面积等于一条直角边长等于圆半径，另一条直角边长为圆周长的直角三角形面积。”[11]据推测，阿基米德通过以下方法发现圆面积公式：如图2所示，将圆从圆心开始直到边缘分成一些细窄的同心圆环，并将这些同心圆环逐一展开叠成一个直角三角形，将圆无限细分时，圆面积与直角三角形面积近似相等。

3开普勒与圆面积公式

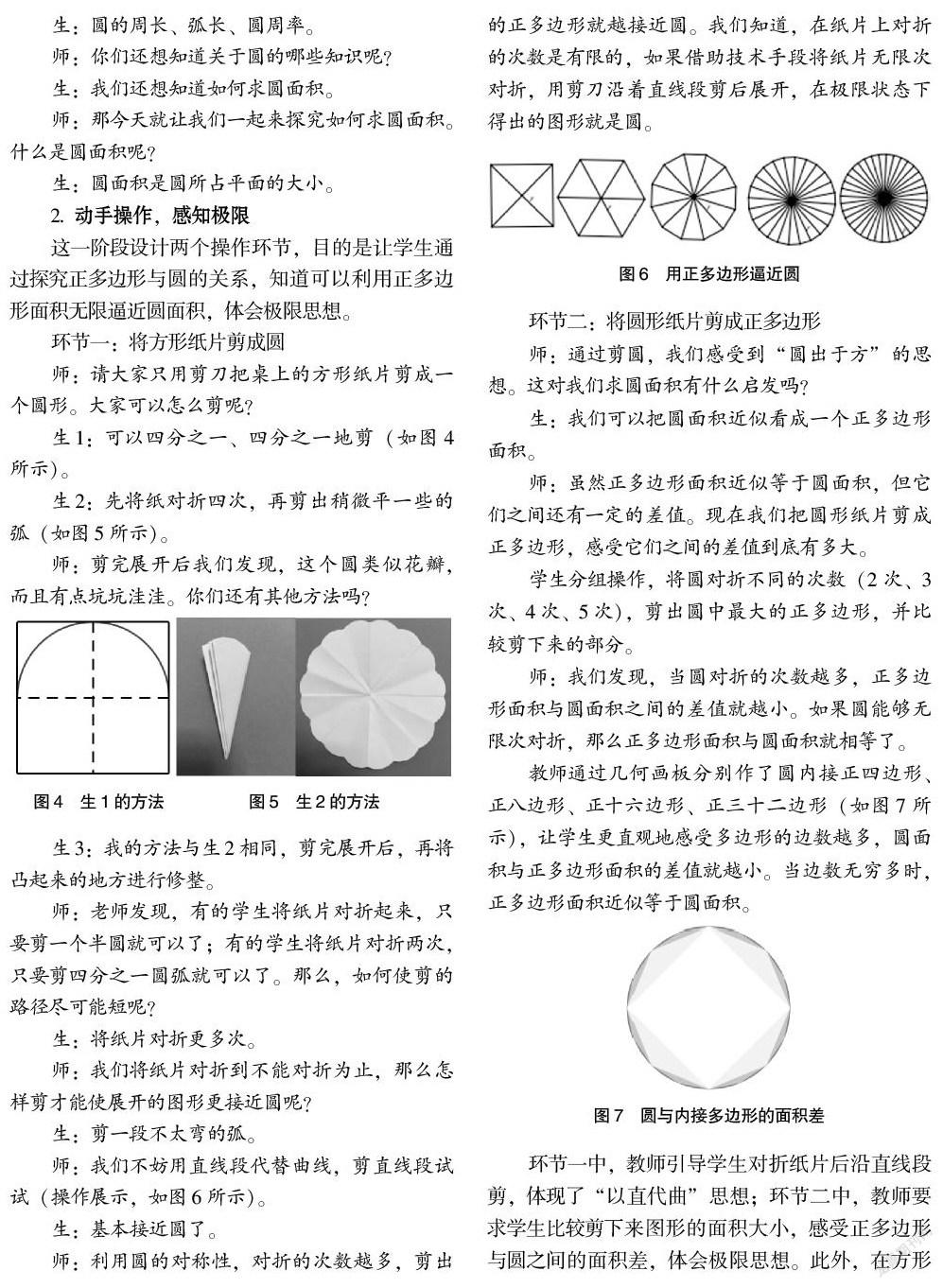
17世纪，德国著名天文学家、数学家开普勒在自己的婚礼上，仍思考着葡萄酒桶体积的算法。要解决这个问题，就要先求出圆面积公式。如图3，开普勒将圆分割成一些小扇形，分割得越细，小扇形就越接近以圆心为顶点、半径为高的小三角形。依次将这些小三角形转化为等底等高的小三角形，拼起来就得到一个直角三角形。在极限的情形下，该直角三角形面积等于圆面积[12]。

本课注重联系实际，在学生原有知识和生活经验的基础上引入圆面积概念及方法;在分析交流环节中，融入刘徽的割圆术、阿基米德的同心圆法、开普勒的分割变形法等相关数学史，并将它们作为阅读材料，引导学生观察、分析、推理，在教学过程中渗透“化曲为直”“以直代曲”“无限逼近”等数学思想，培养学生的直观想象能力和逻辑推理能力。

1复习旧知，引入新课

在教学之前，学生已经学习了圆的概念、圆的周长、弧长等内容。教师通过简短的问答，既能帮助学生回顾之前所学内容，又能很快引入本节课的课题。

师：在前几节课中，我们已经学习了圆的什么知识？

生：圆的周长、弧长、圆周率。

师：你们还想知道关于圆的哪些知识呢？

生：我们还想知道如何求圆面积。

师：那今天就让我们一起来探究如何求圆面积。什么是圆面积呢？

生：圓面积是圆所占平面的大小。

2动手操作，感知极限

这一阶段设计两个操作环节，目的是让学生通过探究正多边形与圆的关系，知道可以利用正多边形面积无限逼近圆面积，体会极限思想。

环节一：将方形纸片剪成圆

师：请大家只用剪刀把桌上的方形纸片剪成一个圆形。大家可以怎么剪呢？

生1：可以四分之一、四分之一地剪（如图4所示）。

生2：先将纸对折四次，再剪出稍微平一些的弧（如图5所示）。

师：剪完展开后我们发现，这个圆类似花瓣，而且有点坑坑洼洼。你们还有其他方法吗？

生3：我的方法与生2相同，剪完展开后，再将凸起来的地方进行修整。

师：老师发现，有的学生将纸片对折起来，只要剪一个半圆就可以了;有的学生将纸片对折两次，只要剪四分之一圆弧就可以了。那么，如何使剪的路径尽可能短呢？

生：将纸片对折更多次。

师：我们将纸片对折到不能对折为止，那么怎样剪才能使展开的图形更接近圆呢？

生：剪一段不太弯的弧。

师：我们不妨用直线段代替曲线，剪直线段试试（操作展示，如图6所示）。

生：基本接近圆了。

师：利用圆的对称性，对折的次数越多，剪出的正多边形就越接近圆。我们知道，在纸片上对折的次数是有限的，如果借助技术手段将纸片无限次对折，用剪刀沿着直线段剪后展开，在极限状态下得出的图形就是圆。

环节二：将圆形纸片剪成正多边形

师：通过剪圆，我们感受到“圆出于方”的思想。这对我们求圆面积有什么启发吗？

生：我们可以把圆面积近似看成一个正多边形面积。

师：虽然正多边形面积近似等于圆面积，但它们之间还有一定的差值。现在我们把圆形纸片剪成正多边形，感受它们之间的差值到底有多大。

学生分组操作，将圆对折不同的次数（2次、3次、4次、5次），剪出圆中最大的正多边形，并比较剪下来的部分。

师：我们发现，当圆对折的次数越多，正多边形面积与圆面积之间的差值就越小。如果圆能够无限次对折，那么正多边形面积与圆面积就相等了。

教师通过几何画板分别作了圆内接正四边形、正八边形、正十六边形、正三十二边形（如图7所示），让学生更直观地感受多边形的边数越多，圆面积与正多边形面积的差值就越小。当边数无穷多时，正多边形面积近似等于圆面积。

环节一中，教师引导学生对折纸片后沿直线段剪，体现了“以直代曲”思想;环节二中，教师要求学生比较剪下来图形的面积大小，感受正多边形与圆之间的面积差，体会极限思想。此外，在方形纸中剪圆，本质上是从外侧逼近圆;而在圆形纸中剪正多边形，则是从内侧逼近圆，体现了阿基米德的双侧逼近法。由于这部分内容偏难，因此不作为学生在课堂上的阅读材料，而是融入到他们的实际操作当中。

3转化图形，推导公式

师：从圆中剪出正多边形的过程与我国古代数学家刘徽的割圆术十分类似。材料一（多媒体放映，略）介绍了刘徽利用圆内接正多边形面积无限逼近圆面积，推导出圆面积公式，并求得圆周率的近似值。有没有同学会翻译刘徽的经典名句“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣”？

生4：割得越细，剩下的面积越少;割了又割，到最后不可以割时，正多边形面积就和圆面积一样了，差值为零。

师：很好！通过动手剪圆操作和刘徽割圆术的启发，我们可以利用正多边形面积近似替代圆面积。而在极限的状态下，正多边形面积就等于圆面积。那么，怎样求正多边形面积呢？

生5：先将正多边形沿半径分割成许多小的等腰三角形，然后展开，最后将这些小三角形倒插起来。

师：很好的思路！老师现在把一个正多边形剪成16个小三角形。你能给大家演示如何将这些小三角形倒插起来吗？（生5演示小三角形倒插过程，略）请问倒插起来后得到的是一个什么图形？

生5：平行四边形（如图8所示）。

师：这个平行四边形的底和高分别是什么？

生5：它的底近似等于圆周长C的一半，它的高近似等于圆的半径r，所以平行四边形面积近似为S=12Cr。

师：当圆被分割得越来越细时，平行四边形面积就越来越接近圆面积。在极限的情形下，平行四边形的底等于圆周长C的一半，平行四边形的高等于圆的半径r，其面积为S=12Cr，这也是圆面积公式。

教师书写圆面积公式的推导过程：S=12Cr=12·2πr·r=πr2

学生拼接圆形的方法是将无限接近于圆的正多边形面积转化为平行四边形面积，与刘徽的割圆术具有异曲同工之妙。这与课本上将圆分割成许多小扇形，再将这些小扇形直接拼成近似平行四边形的方法不同：课本上的方法所拼成的图形面积始终等于圆面积，其形状是近似的平行四边形;而学生的方法所拼成的图形是真实的平行四边形，其面积是圆面积的近似值。

师：还有其他推导方法吗？

生6：将正多边形沿半径分割成许多小的等腰三角形，求其中一个等腰三角形的面积，再乘三角形的个数就可以了。

师：很好的思路！假设我们将正n边形分割成n个相同的小三角形。每个小三角形的底边为a，用C正表示正n边形的周长，那么C正与a有何关系？

生6：a=C正n。

师：若设每个小三角形的高为h，则它的面积S△是多少？

生6：S△=12·a·h=12·C正n·h。

师：那么，正n边形的面积是多少？

生6：nS△=12·C正n·h·n=12C正h。

师：我们通过剪纸操作可知，当正多边形的边数越多时，正多边形周长C正就越接近圆周长C，小三角形高h也越接近圆半径r（PPT演示，如图9所示）。在极限的情形下，正多边形周长C正变成了圆周长C。此时，正多边形的面积是多少？

生：S=12Cr，这就是圆面积。

上述虽然没有采用拼图方法，但每次割圆之后计算每个小三角形的面积并将其相加，得到正多边形的面积，实际上是将开普勒的分割变形法置于求极限的过程之中。

师：在推导圆面积公式时，我们运用了数学中著名的极限思想。不论是将圆转化为平行四边形，还是转化成若干个小三角形，都是用直线代替曲线，这也是“以直代曲”数学思想的运用。

教师播放刘徽割圆术的微视频，让学生进一步感知极限思想。此环节后，教师又展示了多个生活中“以直代曲”的例子（如图10所示），让学生感受生活中处处有数学。

4.重温经典，交流分享

在数学史长河中，虽然早已有关于圆面积计算公式的记载，但仍然有许许多多数学家出于对数学的热爱，不断创造新方法来探索圆面积公式。本环节让学生回顾历史，重温经典。在阅读历史材料（多媒体放映，略）中两位数学家推导圆面积公式的小故事后，教师要求学生根据图形的变化，交流分享数学家推导圆面积公式的过程。

生7：将圆想象成无数个同心圆套在一起，然后沿半径剪开，再沿着剪开的地方“掰开”，就可以近似得到一个等腰三角形。等腰三角形的底即圆的最外圈，其长度就是圆的周长C，而高就是圆的半径r，可以得到圆面积公式S=12Cr。

生7：半径不动，把每个同心圆都拉直，还可以近似得到一个直角三角形。

教师动画演示，略。

师：阿基米德将圆分割成无数、无限细的同心圆环，这样的极限思想让人佩服。在我们课本的第一节里有一句话“点动成线，线动成面”，这其中也蕴含着极限思想。

生8：先将圆分割成无数个极小的扇形，再把这些扇形展开铺在一条直线上，平移它们的顶点，使面积不变（即等积变换），得到新三角形的底即圆的周长C，高即圆的半径r，可得圆面积公式S=12Cr。

教师动画演示，略。

师：同学们你们看，开普勒在自己的婚礼宴会上竟将注意力放在一个葡萄酒桶上，可见他对数学已经达到了痴迷的程度。

在交流分享环节，教师将讲台交给学生。学生通过阅读历史材料，自主探究，进行猜想、推理，升华他们对圆面积公式的认识。在学生讲解之后，教师进行动画演示，让学生直观感受推导圆面积公式的动态过程，体验极限思想。

5讲解例题，总结回顾

本环节中，教师用例题进行回顾。题1是《九章算术》方田章圆田问题“今有圆田，径十步，问为田几何？”。教师要求学生将问题译成现代汉语，并自主解答。题1后是关于圆面积公式的若干应用问题。其中有一题将圆面积与圆周长联系在一起：已知一个圆的周长为628米，求这个圆的面积。教师提示学生可以利用半周长乘半径方法求解。

在课堂小结环节，教师让学生说出最喜欢的数学家或求圆面积的方法，并谈谈自己在这节课中感受到的數学思想。同时，为了延续学生学习数学史的热情，教师可以要求学生课后向家长介绍圆面积公式的探索过程，锻炼学生的语言表达能力。此外，还可以让学生查阅意大利数学家卡瓦列里的棉线法以及其他求圆面积不同的方法，感悟数学家对真理孜孜不倦的探究精神。

课后，笔者对43名听课学生进行了问卷调查。有42名学生表示喜欢本节课中数学史的融入，认为对其学习圆面积公式有较大帮助。关于圆面积公式的不同推导方法，21名学生喜欢刘徽的割圆术，10名学生喜欢阿基米德的同心圆法，10名学生喜欢开普勒的分割变形法，还有2名学生喜欢将圆割成三角形拼成平行四边形的方法。关于难以理解的方法和仍存在的困惑，8名学生认为他们没有难以理解的方法和困惑;8名学生对割圆术的理解比较困难，因为正多边形始终无法与圆完全重合，且他们对割圆术中用到出入相补原理没有完全理解;9名学生对同心圆法的理解比较困难，因为展开图形的形状呈“阶梯状”而并非是严格的三角形;4名学生对分割变形法的理解比较困难，因为三角形的底边仍是曲线;14名学生对棉线法的理解比较困难。关于课堂中印象深刻的环节，17名学生对剪圆、剪多边形的动手操作印象深刻，6名学生对自主推导公式的过程印象深刻，10名学生对数学家的不同推导公式方法印象深刻，10名学生对微视频、动画等印象深刻。对于“你认为这节课中，相关数学史知识给你什么帮助与启示”问题，有的学生认为，这节课让他们知道了要勇于创新，而不是拘泥于他人的方法，而且图文并茂的方式有助于直观理解问题;有的学生认为，数学来源于生活和无数次的实践，反复推敲才能得出大家熟知的公式;有的学生认为，三种圆面积的推导方法，充分体现了人类永无止境的探索精神;还有的学生认为，做数学题不能只是简单地套用公式，而是要理解如何推导、如何运用，这才是做数学题的核心。

在本节课中，融入数学史的价值主要体现在以下几个方面。

第一，历史上不同时空的数学家都对圆面积公式做过证明。本节课运用了历史上两种推导圆面积公式的方法，一是刘徽的割圆术，二是开普勒的分割变形法。同时，阅读材料还呈现了阿基米德的同心圆法。学生在本节课中充分感受到了求圆面积公式的“方法之美”。

第二，通过用方形纸片剪圆和圆形纸片剪正多边形的操作活动，学生理解了正多边形与圆之间的关系，体会到了“以直代曲”“圆出于方”的转化思想和极限思想。教师借鉴推导圆面积公式的历史，引领学生通过剪纸操作发现割圆术，实际上通过数学史营造了“探究之乐”。从学生课后的反馈表明，大多数学生喜欢这一环节。

第三，数学并不是孤立的一门学科。本节课将历史、语文等多门学科融合在一起，如教师让学生在数学課堂上翻译古代汉语。课堂上所展示的不同时空数学家的圆面积公式推导方法，让学生认识了数学文化的多元性。因此，通过数学史的融入，教师展示了数学的“文化之魅”。此外，学生也能体会到古代数学家求真、创新、执着的精神，达成了“德育之效”。

参考文献：

[1]孟兆山.“圆的面积”教学实践与反思[J].小学教育科研论坛，2004（6）：54-55.

[2]吴剑春，马凤枝.“圆的面积”设计及评析[J].小学教育科研论坛，2004（7/8）：121-123.

[3]张平.课题：探索圆的面积公式[J].教育实践与研究（A），2008（7/8）：88-92.

[4]刘韵.《圆的面积》课堂教学实录[J].现代教育论丛，2007（4）：84-87.

[5]李艳秋.《圆的面积》教学设计[J].小学教学研究，2014（10）：75-76.

[6]顾文彬.“圆的面积”教学设计及评析[J].小学教学参考，2003（9）：37-39.

[7]余艳红.将渗透数学思想进行到底：以苏教版第十册“圆的面积”一课教学为例[J].数学学习与研究，2014（22）：100-101.

[8]张纪存.《圆的面积》教学设计：“自学指导式”教学模式[J].课程教育研究，2018（20）：132.

[9]孙红叶.小学教师运用数学史的困难及解决途径：以“圆”一章为例[D].成都：四川师范大学，2014.

[10]郭书春汇校.九章算术[M].沈阳：辽宁教育出版社，1990.

[11]汪晓勤.HPM：数学史与数学教育[M].北京：科学出版社，2017.

[12]汪晓勤.数学史与数学教育[J].教育研究与评论（中学教育教学），2014（1）：8-14.