巧借“四重四学” 提升思维能力
缪晶

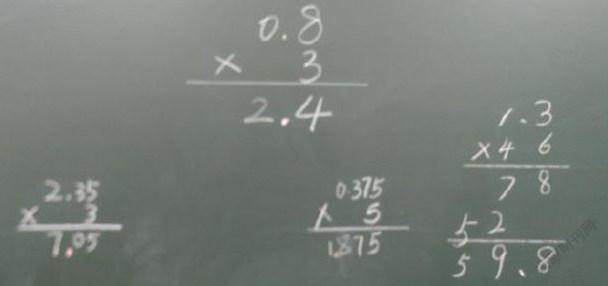
【摘 要】思维的深度和广度是思维的两个重要特征,而发展思维的深度和广度就是数学教学的重要任务。计算教学中如何有效启迪学生思维?我校推出“四重四学”教学模式,“四重”即重师与生关系,重教与学的互动,重生与生的关系,重生与文本对话;“四学”即学生在新知学习的过程中经历“预学-研学-固学-延学”的四种学习形式,通过师、生与教学资源之间的一种有效互动,让课堂成为高效和谐的学习共同体,为计算教学开创一条幸福大道,有效提升学生的思维能力,现就苏教版五年级上册《小数乘整数》谈谈我们的收获。
【关键词】“四重四学”;提升;思维能力
一、预学环节问题引领探新知
斯托利亚尔指出:数学教学是数学思维活动的教学。怎样在数学教学中发展学生的思维能力?问题引领是一种非常有效的策略。“四学”的预学环节,就是由教师设计一个或一串相关的问题,引领学生进行新课学习前的思考、尝试,在新课学习前收回预学单,了解学生想法,做到先学后教,有针对性地进行教学。如《小数乘整数》一课,预学单上设计的问题就是:0.8×3你是怎样算的?用你自己喜欢的方式来表示你的想法。收回的预学单出现以下六种不同的想法。
学生在思考后得出的这几种想法着实令人惊喜,预学单的出现,无疑让抽象笼统的预习作业有了具体形象的载体,作为学生课前的自主学习行为,孩子的思维跃然纸上,对课堂教学的影响不言而喻,在课堂上,教师有意识按上面六种方法的顺序安排汇报,在教师的引导下由具体到抽象,数形结合,让学生明白:0.8乘3就是在计算8个0.1乘3,也就是24个0.1,所以积是2.4,使算理更为明晰,多种想法的交流拓宽思维的广度,培养了学生数学理解能力。
二、研学固学对比总结练思维
学生对新知识的学习是以旧知识为基础的,新知识要么是在旧知识的基础上引申和发展起来的,要么是在旧知识的基础上增加新的内容,或由旧知识重新组织或转化而成的,计算教学尤其如此。本节课,整数乘法笔算方法就是小数乘整数计算方法的基础,小数点的点法是新知,有过预习的课不等于所有的知识学生都能通过预习解决,“积的小数点怎么点?为什么?”是本节课的难点,通过猜想——验证——说理,弄清这个理,知其然而知其所以然地学习才有助于运算能力的提升及思维的发展,由于有效的预学节约许多思考的时间,研学环节就可将大块的时间用在“明理”上。在新授初步结束后,教师将例题和练习的竖式一同出现在黑板上:
教师:观察这四道算式,你能大胆地猜想一下:积的小数位数和乘数的小数位数有什么关系?
学生:我发现乘数是几位小数,积就是几位小数。
教师:似乎有点道理,我们再来看看下面这道题。
出示: 猜一猜下面算式的积是几位小数,再用计算器验证。
2.8×53= 4.76×12= 103×2.5= 4×0.25=
(学生用计算器计算并汇报结算结果)
教师:计算器验证果真和大家猜想的一样,那谁根据今天的学习,说说为什么一位小数乘整数,积就是一位小数?两位小数乘整数,积就是两位小数……
结合前面的说理练习,学生很快就能发现:一位小数乘整数就是在算有几个0.1,所以积也是一位小數;两位小数乘整数就是在算有几个0.01,积就是两位小数……计算计算,就是在计算有几个这样的计数单位。随后总结出笔算小数乘整数的方法:小数乘整数先按整数乘整数来算,最后看乘数是几位小数,积就是几位小数。对比发现是数学教学最好用的方法,在对比中更容易看出知识间的联系,新知得以巩固,思维得以深入。
三、延学伸长贯通经脉促提升
同一个领域的数学知识都不是独立存在的,有其内在的联系,沟通知识间的联系不是复习课才做的事,每节课不仅要学习本节课的内容,还应着眼长远。“四学”中的“延学”就是以本节课的知识为载体,沟通知识间的联系,挖掘隐性知识,或将同类知识进行对比,或对知识追根溯源,注重知识的系统性,强化思维的深度,促进学生综合素养的发展,使学生对旧知、新知组建稳定、清晰、系统的认知结构,加深对数学计算知识的记忆和理解,实现对知识的再发现。
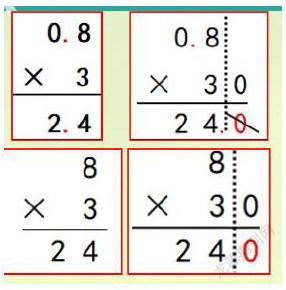
本课教学,学生对笔算0.8乘3时,3为什么要和8对齐,而不是和整数部分的0对齐?持有一定想法,即:为什么笔算小数乘法时要末位对齐,而不是相同数位对齐?于是,延学环节设计了这样几道和例题类似的笔算题,让学生计算后引导学生对比辨析:
纵观全局
教师:大家看这几道算式,笔算时有什么共同点?
学生1:8都是和3对齐的。
学生2:计算时都可以看作8乘3来算。
局部引导
教师:我们先看下面过去学习的这两道竖式(8×3、8×30),为什么右边的竖式可以把3和8对齐,0放一边?
学生1:为了计算简便。
学生2:将30看作3个十,所以直接算3乘8,再在积后面添0。
教师:再看0.8×30这个竖式,它为什么也可以简便?
学生:把30看作3个十啊!
再次观全局引导
教师:想想,它们计算时为什么都可以看成8乘3来算?
思考片刻后教师引导,学生整理总结:
学生:0.8×3看作8个0.1乘3,0.8×30看作8个0.1乘3个十,8×3就是算8乘3,8×30看作8乘3个十,都可以看作8乘3,只不过有的是算多少个0.1,有的算多少个1,有的算多少个十。
教师:是啊,不管是整数乘整数,还是整数乘小数,都是计算一共有几个这样的计数单位,我们都可以把它看作整数来算,现在你知道为什么可以这样对齐了吗?
学生:哦!都是看成整数来算,所以按整数乘法对齐!
教师:你们的“哦”真是太美妙了!最后再根据它们的意义,看看是几个几来点小数点或添0。现在还要纠结3究竟要和谁对齐吗?
抓住本质,利用对比进行本源探究,既贯穿知识体系又训练思维向纵深发展,边学边悟,扎扎实实。
“四重四学”教学模式在课堂中学生不仅做到“学”与“思”,还能“说”与“评”,由于经常鼓励学生提出问题,表达自己对问题分析的思路以及问题解决的方法,学生语言表达能力、逻辑思维能力大幅提升,变被动学习为主动学习,变浅层学习为深度学习,让思考成为一种习惯,学生思维能力得到了较大的发展,解决问题的素养与能力得到了提高,当计算教学都能由“冰冷的美丽”转化为“火热的思考”,那么学生思维能力的提升也就水到渠成了。
参考文献:
[1]张凤霞.浅谈小学数学中学生思维能力的培养[A].第四届世纪之星创新教育论坛论文集[C].2016.
(责任编辑 袁 霜)

