体系观点定问题 深度学习真发生
李波 赵小丽
摘要:教师要有体系思想,要盡可能地在课堂教学中,带着全面、联系的眼光,创设带有体系思想的关键问题,从而引发学生对所学内容更集中、更深入地研究和探索,促进深度学习的真发生。
关键词:教材体系;关键问题;个性落实;深度学习
数学是充满强烈内部联系的学科,作为教师要善于遵循或挖掘这种内部联系。也就是说教师要有体系的思想,要尽可能地在课堂教学中,带着全面、联系的眼光创设带有体系思想的关键问题,从而引发学生对所学内容更集中、更深入地研究和探索,促进深度学习的真发生。笔者和所在的教研团队对此进行了多年的教学实践研究,下面是在立体图形特征的系列教学实践中的一些思考与收获。
一、立足教材体系,确定关键问题。
1.教材的编排体现了“体系”结构
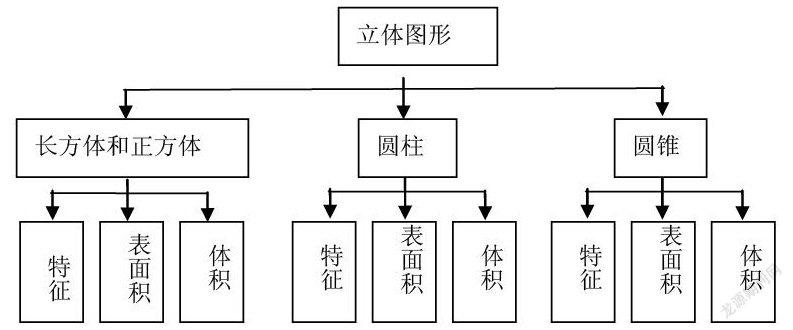
现行小学数学教材中,主要学习四种立体图形,分别是长方体、正方体、圆柱和圆锥。它们都是规则的几何体,是构成现实世界的基本元素。前两者的内容安排在五年级进行教学,后两者在六年级下期进行。
纵观教材,四种立体图形均是通过观察大量的实物、抽象出立体图形的特征,从而归纳和总结出立体图形的基本研究思路:一个立体图形可以从棱、顶点、面三个方面进行研究。随着四种立体图形的学习不断深入,不仅知识和技能的层次在逐步提高,而且学生研究立体图形的基本思路也在逐步熟练、入微和拓展。
横看教材,四种立体图形的主要内容均以图形的特征和测量为主。其中图形的形成过程是理解表面积和体积概念的关键,图形的特征是探究图形的表面积和体积计算公式、理解公式的支撑点,而面积和体积的计算及应用又强化了图形的特征。
通过纵横对比,可以看出四种立体图形的特征学习内容,不是孤立的,而且有着胶着的联系,你中有我,我中有你,互相依存。所以,在教学中教师一定要有大的体系观:不仅要注重学生的知识和技能体系建构,更要从整体入手,放眼到学生研究能力的培养和思想方法体系的完善的层面。
2.学生的深度学习需要“体系”建构
五六年级的学生,已经对立体图形有了感性的认识,也经历了平面图形的研究过程。有了一定的空间观念,但是依然对直观的依赖性比较强,学生容易理解图形的外显特征,对于内隐的图形、各部分关系、图形与图形之间联系的认识还缺乏理性分析,尤其三个维度之间自由的切换对学生来说异常的困难。学生常常会出现棱长总和、表面积、体积概念混淆,计算时公式选择错误的现象,恰恰说明了这一特点。因此,“数学概念和公式只有在关系和结构中才有意义,才能保持长久记忆。”
基于以上思考,在立体图形的特征的教学实践中,我们以“这种立体图形分别和哪种平面图形有联系?有什么联系?”、“这种立体图形有什么特征?”“影响这种立体图形的大小的因素有哪些?”这样几个统领三节课的“关键问题”为导向,牵一发而动全身,将学生置身于数学概念的关系与结构之中,促使学生主动思考、沟通立体图形和平面图形的联系,在“点、线、面、体”的不断转换中抽象概括出立体图形的特征。
二、依据关键问题,驱动深度学习
虽然这三种图形特征的共性突出、密不可分,但是每个图形又极具特色、个性十足,并且在学习时处于不同的阶段,学生的认知经验也有很大差异。因此我们在教学实践中不仅通过以上“关键问题”把握三节课的共性,而且力求使“关键问题”在每节课中能够个性落实,生成一种多线交融,层层递进的数学系列课堂结构。
用运动的观点来研究图形的特征,是帮助学生从平面走向立体,从二维空间观念发展到三维空间观念的有力法宝。整节课紧扣关键问题,围绕着“动”展开,通过学具操作、想象“四个平面图形绕着小棒旋转一周,留下的轨迹是什么图形?”结合课件帮助学生将脑海里模糊的、抽象的空间想象化为直观的动画演示,体验“面动成体”的过程,突破教学难点。并且通过游戏的形式引出“平移会形成柱体”,让学生深入体会运动与图形特征之间的内在联系,为学生“面”和“体”的空间对比更加鲜明。
【案例】《圆柱的认识》教学片断(2):“剖”体为面
生:圆柱的这个面,(沿高)剪开后是一个长方形。
师:他说的是哪个面?
生:(生指)这个弯曲的面。
师:这个特殊的面就是圆柱的侧面,它是一个曲面。。
师:他这一剪把圆柱的侧面变成了一个——?
生:长方形。
师:对,这一剪非同小可,他把很难研究的曲面转化成了长方形,我们非常熟悉的一个平面图形,这就是化曲为直。
在动态认识几何体的形成过程的基础上,引导学生以小组为单位,通过看、滚、剪、切等多种方式从多种角度去探索圆柱的特征,研究侧面的特征时,很多学生亲自动手将它们的侧面剪开,学生在操作中通过观察、抽象、想象,感受“化曲为直”的数学思想,为进一步思考圆柱侧面、底面及其之间的关系,从而更加丰富对圆柱特征的理解。
【案例】《圆锥的认识》教学片断(1)
师:长方体、正方体、圆柱和圆锥,每一种立体图形都和平面图形有联系。前三种立体图形我们已经学过了,请大家想一想,它们分别和哪种平面图形有联系?有什么联系呢?
生:长方体是由六个长方形围成的。
师:这个同学从“围”的角度,说明了长方体和长方形之间的关系:长方体是由六个长方形围成的。
生2:长方体可以由长方形平移得到。
师:这个同学从“动”的角度,也说明了长方体和长方形之间的关系:长方体可以由长方形平移得到。
……
师:前面的三种立体图形我们都可以从两个角度找到它们和平面图形的联系,继续想象,今天我们研究的圆锥又和哪个平面图形有联系?有什么联系?你又能发现点什么?可以结合教师提供的材料进行研究。(如右图)
在活动中学生又遇到了一些新的问题,比如:“顶点到底面的线段有这么多,为什么只有顶点到底面圆心的距离才是圆锥的高?”大家知道线与面的垂直,在高中立体几何中也是个难点,在我们小学阶段要想理解是特别困难的,但是三角形的旋转让我们孩子拥有了一双“透视眼”,看到了线与面的垂直关系。比如,在“围”的过程中提出质疑“为什么只有扇形和小圆才能围成圆锥,其他的素材都不行?”
几个小话题,都由本节课的关键问题而产生,没有人为的提升知识的难度,但学生普遍感受到了智力的冲刺与挑战。究其原因是源于是教师抓住了圆锥的在整个立体图形体系中的位置和它的本质特征,扣住了知识的节点,切准了学生学习的疑点。学生在解决问题的过程中逐步发现新的小问题,通过不断地发现解决问题逐步完善知识能力体系,在思考和建构中引导学生深度学习。
数学教学的每一个内容都不是孤立存在,而是纵横联系发展的。教师在钻研课堂教学时,要善于把握知识体系结构,确定适合促进学生思考和学生发展的关键问题,来指导教学实践,从而促进学生深度学习的真发生。
河南省教育科学规划“一般课题 + 几何画板与小学数学教学深度融合的研究 + (2017)-JKGHYB-0886”。

