风力发电系统故障建模与仿真

吴天霞，王 欣，田盛华

(湖南工业大学电气与信息工程学院，湖南 株洲 412007)

0 引言

随着风力发电技术的飞速发展以及风电机组单机装机容量的不断增加，其结构复杂性和控制方法的多样性使得故障的发生率也随之增加。近些年来对于风力发电系统的故障诊断与容错控制逐渐在国内外成为研究热点。国内对风电发电的研究大多是基于国外各公司实验室开发的软件，常用的如Fast、Bladed、Adams等软件。文献[1-2]基于Fast软件分别对发电机故障时变桨速率对风电机组载荷的影响规律和叶片卡死故障紧急停机工况下的风机动态特性进行了研究；文献[3]基于Bladed软件针对双馈风电机组传动链电网故障过程中可能存在的扭振问题进行了研究；文献[4]基于Adams软件建立了正常和故障状态下变速器齿轮动态模型，并探讨了无传感器诊断在风力发电机故障诊断中的应用。利用Fast、Bladed软件所搭建的风力发电系统是经过长期研究得到的整体模型，使用者若要根据研究需要对模型进行调整，调整过程复杂，且易破坏模型的整体性能。通过Adams软件搭建风电机组故障模型大部分情况下需要衔接Matlab进行联合仿真，以便能更精确、直观地进行仿真分析。这使得仿真过程变得繁琐，容易出现操作误差。

基于上述分析，本文以2 MW风力发电系统为背景，基于Matlab仿真软件建立了风力发电系统动态模型，并在此基础上搭建了一个可模拟风电机组传感器故障、执行器故障，和可用于故障检测与容错控制的模型。该模型具有灵活性强的特点，可根据研究需要在所搭建风电系统中增减不同类型的故障以及调整故障强度，运用此模型可在实验室对风力发电系统进行故障检测与容错控制研究。

1 风力发电系统建模

风力发电的原理是将风能转化为机械能的过程，也是将一次能源和二次能源进行能量转换的过程。整个风力发电系统可用图1所示的几个相互关联的子系统表示，即：气动力系统、传动系统、发电机系统、变桨系统[5-19]。

图1 风力发电系统各子系统关联结构图Fig.1 Subsystem correlation structure diagram of a wind turbine generation system

1.1 空气动力系统

由空气动力学可知，风机转子从风能中捕获的功率为

(1)

式中：ρ为空气密度；R为风轮半径；V为风速；Cp(λ,β)为风能功率系数；λ为叶尖速比；ωt为风机转子转速。

根据贝兹理论，风能功率系数Cp和桨距角β、叶尖速比λ的关系如下：

(2)

1.2 传动系统与发电机系统模型

在忽略传动链内部和发电机部分电力电子变换器动态过程的条件下，可用如下简化的一个1阶方程表示：

(3)

1.3 变桨系统

目前在大中型风力发电系统中变桨距系统大多采用电-液伺服系统，也可理解为是控制器产生的参考桨距角跟实际桨距角之间的动态关系，可近似于1阶动态系统：

(4)

式中：τβ为时间常数；βref为参考桨距角。

1.4 风速序列

本文在仿真过程中使用的风为预定义的风速序列，如图2所示，该风速为基于凯马(Kaimal)频谱的随机风速模型下桨距和风机转速的波动图。设定基本风速为15 m/s，湍流强度为12%。所搭建的2 MW风力发电系统所涉及的参数如表1所示。

图2 仿真时的风速序列图Fig.2 Wind speed sequence diagram during simulation

参数数值风轮转动惯量/(106 kg·m2) 5.4电机转动惯量/(kg·m2) 97.5风轮额定转速/(r·min-1) 20传动比90空气密度/(kg·m-3) 1.225 风轮半径/m 70.5额定功率/kW 2000定子额定相电压/V690修正系数0.811定子相数 3电机极对数 2定子绕组电阻 r1/Ω0.016 定子绕组漏抗x1/Ω 0.22转子绕组电阻r2/Ω0.032转子绕组漏抗 x2/Ω 0.14

2 控制系统设置

风速的大小和方向是随机变化的，外力无法控制。但风力发电机组却受切入电网功率、切出电网功率和输入功率的限制，风轮的主动对风以及在运行过程中的故障检测和容错控制都必须能实现自动调节[12]。

在风电机组的控制过程中，为获得理想的输出功率，系统一般工作在图3所示的4个区域：区域Ⅰ，风机启动；区域Ⅱ，功率优化；区域Ⅲ，恒定功率产生；区域Ⅳ，高风速。va、vb、vc分别表示切入风速、额定风速、切除风速。

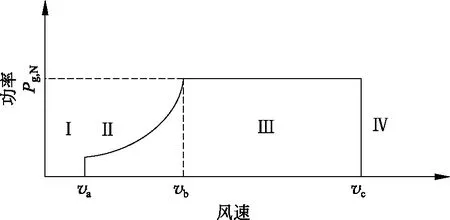
图3 风电机组期望功率曲线Fig.3 Wind turbine expected power curve

当风速低于额定风速时，常采用变速控制的方式；当风速高于额定风速时，常采用变桨控制的方式。变桨控制方式是通过改变桨距角来改变作用在风轮上的气动扭矩，进而使功率保持在额定值(Pg,N)。为更准确地模拟故障的影响，对系统进行了PID变桨距控制。

经典的PID控制器具有结构简单、调节方便、控制稳定等优点，最早在工业控制领域被广泛应用。现装机的风力发电机组的控制系统最常见的控制器就是PID控制器，其基本原理是将系统偏差的比例、积分及微分按一定的规律进行线性组合，最终构成对象的控制量，进而实现控制作用。其控制的高可靠性足以使整个风电系统达到较好的稳定性。

基于PID的变桨控制规律如下：

(5)

式中：u(t)为控制量；kp为比例增量；ki为积分增量；kd为微分增量；e(t)为输入与输出偏差。

3 故障建模与仿真

故障通常可定义为，系统在正常条件下，至少有1个特性或参数发生不期望的偏差，即所有能降低系统整体性能的不期望的变化[12]。故障不同于失效，失效是系统完全崩溃，是在特定运行条件下，系统实现所要求的功能的完全中断；而故障通常是指系统的失灵，可看作在特定运行条件下，系统实现所要求的功能的短暂中断或系统性能的降低。系统故障可分为3类，即传感器故障、执行器故障、被控对象故障。其中系统最常出现的故障为传感器故障与执行器故障。本文主要通过对风力发电系统中发电机部分的传感器和执行器故障进行模拟，建立用于模拟故障检测和容错控制的模型。

风力发电系统中发电机的传感器有发电机转速传感器，执行器有发电机的转矩传感器[16]。将可能发生的故障分为如下5类：1)传感器恒偏差故障；2)传感器恒增益故障；3)执行器恒偏差故障；4)执行器恒增益故障；5)混合故障。

3.1 传感器故障

1) 传感器恒偏差故障。

系统在60 s时发电机转速传感器发生恒偏差故障，此时ωgout=ωgin+Δωg，其中Δωg=1 rad/s。

2) 传感器恒增益故障。

系统在60 s时发电机转速传感器发生恒增益故障，此时ωgout=ζωgωgin，其中ζωg=0.51。

传感器故障时风力发电系统的发电机转速ωg与系统输出功率P如图4所示。

图4 传感器故障时发电机转速与输出功率 Fig.4 Generator speed and output power under sensor faults

在风力发电系统中发电机的转速传感器将发电机转速测量值传送给发电机转矩控制器，发电机转矩控制器的作用是尽可能地使风能利用系数最大限度地接近最佳值，从而捕获到最大的风能以得到较多的能量输出。由图4可看出，在正常情况下风电系统的输出功率在2 MW左右小幅度波动，输出稳定。系统在60 s发生传感器故障情况后，输出功率发生较大幅度波动，特别是在传感器发生转速恒增益故障期间，除发电机转速发生恒增益外，系统输出功率最大值与最小值差高达1.5 MW，系统处于极度不稳定状态，系统输出能量的质量明显降低。由此可见对实际运行的风电系统而言，若发生此类故障，对系统进行故障诊断和容错控制是十分必要的。同时，仿真结果也验证了所搭建的模型能较好地模拟故障，为故障诊断与容错控制研究提供了基础。

3.2 执行器故障

1) 执行器恒偏差故障。

系统在100 s时发电机转矩执行器发生恒偏差故障，此时Tgout=Tgin+ΔTg，其中ΔTg=20 000 N·m。

2) 执行器恒增益故障。

系统在100 s时发电机转矩执行器发生恒增益故障，此时Tgout=γTgTgin，其中γTg=2。

执行器故障时风力发电系统的发电机转矩Tg与叶尖速比λ如图5所示。

图5 执行器故障时发电机转矩与叶尖速比Fig.5 Generator torque and tip speed ratio under actuator faults

在风力发电系统中发电机转矩执行器在发电机转矩控制器控制信号的作用下，能调节风力机转速，保持叶尖速比λ为一定值，即维持风力机在最大风能利用系数下运行，实现最大功率输出。由图5可看出：正常状态下系统能较好地实现最佳叶尖速比的相似追踪，此时风电系统的最佳叶尖速比λ=9.9。系统在100 s发生执行器故障后，发电机转矩与正常情况下相比出现明显的增益与偏差，同时能反映发电机转矩执行器性能的叶尖速比偏离最佳叶尖速比(λ=9.9)。此时系统对最佳叶尖速比的相似追踪能力明显下降，随之将导致系统性能下降。

3.3 混合故障

系统在80 s时发电机转速传感器发生恒增益故障，发电机转矩执行器发生恒偏差故障，此时有：

1)ωgout=ωgin+Δωg，其中Δωg=5 rad/s；

2)Tgout=γTgTgin，其中γTg=2。

混合故障时风力发电系统的系统输出功率P与叶尖速比λ如图6所示。

图6 混合故障时输出功率与叶尖速比Fig.6 Output power and tip speed ratio under mixed faults

在正常运行的风力发电系统中，在任何风速下，为获得最大的风能利用，输出理想的功率，需要调节风力机的转速，使其叶尖速度与风速之比λ保持不变，并满足λ=λopt(λopt为最佳叶尖速比)，使风力发电系统输出理想功率。混合故障是传感器故障与执行器故障的结合，但并不是简单的两个单一故障影响的叠加，实际影响以仿真结果为参考。由图6仿真结果可看出，系统在80 s发生传感器与执行器混合故障后，系统的输出功率比正常情况低2 MW。系统的叶尖速比偏离最佳叶尖速比(λ=9.9)。

由以上仿真分析可知：所搭建的模型在未发生故障时，具有较好的性能；当系统的发电机转速传感器、转矩执行器发生故障时，有时即使是很微小的故障，都将对系统性能造成很大的影响，甚至使系统失去稳定。同时，仿真结果也证明了所搭建的模型能较好地模拟传感器与执行器故障。此时，若想恢复系统性能，需要对系统进行相应的故障诊断和容错控制。

4 结语

本文搭建了2 MW风力发电机组动态模型，仿真结果证明了模型的准确性；在此基础上对风力发电系统的传感器故障和执行器故障进行了模拟，建立了一种可用于模拟风力发电系统故障检测和容错控制的模型。所搭建故障模型中包含不同类型的故障，可在模型上测试不同类型的故障检测和容错控制方案。在预定义风速的作用下，对模型所模拟的传感器故障与执行器故障进行了仿真，仿真结果证明所搭建的故障模型能较好地模拟故障，为后续风力发电系统的故障检测与容错控制研究奠定了基础。