基于PSS/E的风电场优化运行仿真及分析

牟晨东，陈艳宁，顾秀芳，于 迪

(内蒙古工业大学电力学院, 内蒙古 呼和浩特 010080)

0 引言

当前我国能源总体富余，部分行业已经出现了产能过剩情况，风电的发展也已经进入瓶颈期。为此应进一步降低风电场的发电成本，使风电场运行在最优的状态，风电场的优化问题将直接影响着未来风电的发展方向。随着风机制造行业技术的不断发展，目前我国自主研发的风电机组单机容量已经达到6 MW。风电机组单机容量及风电场的装机容量不断增大，必然会导致风电场输送的功率不断增长，风电场集电线路的功率损耗不容忽视。因此，有必要对风电场内部的潮流进行优化。

PSS/E是一款功能强大的电力系统分析软件，可完成如潮流、短路电流、稳定性、等值、可靠性等计算和分析功能。PSS/E软件提供了4种风电机组的通用模型与3种无功功率控制方式[1]，可方便准确地模拟风电场的各种运行状态。文献[2]给出了双馈机组的风电场潮流计算模型，采用了利用转差率求解双馈风机有功功率与无功功率的简化方法。文献[3]详细说明了风电场在潮流计算中对风机节点的处理，阐述了风机控制方式与节点类型的关系，但具体在PSS/E软件中如何实现尚无文献进行详细介绍。文献[4]利用PSS/E软件实现了含有风电场的电力系统的潮流计算，并在此基础上开发了连续潮流计算功能，但对PSS/E风电机设置方法介绍不够深入和详细。文献[5]利用Matlab软件对含风电场的电力系统进行了潮流优化，但其将风电场等效成一个单台机组，对风电场内部的潮流分布没有进行分析。文献[6]在风电场的潮流优化时考虑了风电场的内部结构，但其忽略了风电场的集电线路，在风电机组输出功率较大的情况下存在着一定的误差。文献[7]利用PSS/E软件的优化功能，求解了以全网损耗增量和限流电抗值总和最小为目标函数的优化问题。

本文将结合现有文献，重点分析PSS/E软件中关于风机参数的设置，明确节点类型、控制方式在PSS/E中的设置方法，并结合最优潮流(optimal power flow，OPF)功能讨论风电场的优化问题。

1 PSS/E常规潮流及最优潮流计算方法

1.1 常规潮流与最优潮流

电力系统常规潮流通过求解不平衡非线性方程组来求取电压、功率等未知量。理论上，最优潮流通过形成和求解带有约束条件的优化问题来求解未知量。具体实现上，最优潮流将原有目标函数与约束条件组合为一个新目标函数。

两种潮流计算在控制变量处理上有较大不同：常规潮流中需要多次迭代以确定控制变量是否满足运行要求或其解是否可行;而最优潮流自动调整控制变量以实现所设定目标，因而所需迭代次数较少。

1.2 最优潮流数学模型

最优潮流模型[8]表示为

(1)

式中:x为系统变量；f(x)为目标函数；h(x)为等式约束条件组；g(x)为不等式约束条件组。

目前最优潮流算法主要有简化梯度法、牛顿法及内点法等，PSS/E33 版本提供了基于内点法的OPF功能[9]。内点法就是在其进行寻优计算的过程中，其迭代的解始终在相关可行域的内部进行寻优。

PSS/E33版本目标函数是复合函数，包含显性与隐性两部分。其中显性部分就是在软件界面中设置的目标函数，比如最小燃料成本、最小有功(无功)损耗等；隐性部分带有惩罚系数的目标函数，一般是将不等式约束条件引入目标函数。

最优潮流求解实质上是求解非线性问题。PSS/E33 版本通过引入拉格朗日乘子来解决带有目标函数与等式约束条件的非线性问题。

L(x,λ)=f(x)+λt[h(x)]

(2)

式中：λ为拉格朗日乘子；t为拉格朗日乘子的次数。

内点法将不等式约束条件通过不同方式引入到目标函数中，式(2)变为

L(x,λ)=f(x)+B(x)+λt[h(x)]

(3)

式中B(x)为满足不等式约束的障碍函数。

PSS/E33版本为不等式约束提供了硬约束与软约束两种约束，软约束又分为线性约束与二次型约束。

当不等式约束条件采用线性约束时，在求解过程中则将带有权重的障碍函数引入目标函数，障碍函数的具体表达形式如下：

(4)

式中：m为采用线性惩罚控制的变量个数；x为控制变量当前值；xmax为控制变量的最大取值；xmin为控制变量的最小取值；λm为惩罚系数。

通过在目标中引入惩罚系数，可成比例地反应控制量与极限的偏差。

若将二次型约束用于不等式约束，则将下式带有权重障碍函数引入目标函数：

(5)

若采用硬约束，则将障碍函数B(x)引入目标函数，B(x)表示为

(6)

图1描述了硬约束的约束情况。选择硬约束时，意味着在寻优过程中绝对不允许超出边界；而采取软约束时，则可超出边界，但是要通过运算进行修正。通常控制变量一般选取硬约束，而状态变量选取软约束。

图1 对数障碍函数Fig.1 Logarithmic barrier function

2 PSS/E中风电场潮流计算参数设置方法

2.1 风电机组参数设置方式

在PSS/E33 版本仿真软件中常规发电机组与风力发电机共用一个发电机模型。PSS/E中提供了与风机运行方式相关的控制模式。如何结合风机运行特点处理节点类型、控制方式是本文重点阐述的问题。

2.1.1 双馈风机机端节点类型处理方法

风机节点类型与其控制方式(恒电压、恒功率因数)有关。恒电压控制方式下风机节点类型设置为PV节点。如果发生无功越界的情况，节点类型由PV节点转变为PQ节点，无功出力为上下限值。恒功率因数方式下，节点类型设置为PQ节点[10-12]。

2.1.2 双馈风机有功出力计算方法

目前现有的文献对于风电机组的有功出力有两种处理方法：1)将其处理成与风速成线性关系；2)处理成3次方关系。本文采用第2种方式，即有

(7)

式中：v1、v2、v3分别为风机的切入风速、额定风速和切出风速，m/s；PN为风机的额定功率，W。

通过风功率曲线计算得到的双馈风机有功出力是定子侧与转子侧的有功功率之和。若计算精度要求不高，转子侧的有功功率可忽略，则认为风机定子侧的有功出力Pd等于双馈风机的有功出力P，即有

P≈Pd

(8)

若不忽略转子侧的有功出力，则需要分别求出转子侧与定子侧的有功出力。定子侧有功出力为

(9)

转子侧有功出力为

Pz=-sPd

(10)

式中s为在该风速下的双馈风机转差率。

2.2 双馈风机无功出力计算

由于转子侧与系统交换的无功功率非常小，可认为双馈风机的无功出力等于定子侧的无功出力。但是双馈风机的无功出力与其有功出力及其控制方式有关。

1) 恒电压控制方式。

当双馈风机运行在恒电压的控制方式下时,在其无功的调控范围内风机的无功出力是由系统潮流来决定的。

不考虑风机物理条件约束时，其无功功率的极限仅受有功功率与功率因数的限制：

Qmax,min=±Ptanφ

(11)

考虑风机物理条件约束时，其无功功率的极限受以下3个条件的限制：

① 转子电流的限制。

若双馈风机定子侧输出的有功功率为Pd，则定子无功功率的范围为

(12)

式中:US为风电机组的机端电压；XS为风电机组等值电路中的支路电抗；Xm为风电机组等值电路中的励磁支路电抗；Irmax为风电机组转子侧的最大电流。

② 定子电流的限制。

若双馈风机定子侧输出的有功功率为Pd，则定子无功功率的范围为

(13)

③ 双馈风机的稳定约束。

(14)

由式(12)—(14)可求取双馈风机的无功功率极限。

2) 恒功率因数控制方式。

一定风速下，风机有功与无功功率是固定的，即满足

Q≈Qd=Pdtanφ

(15)

这里的有功功率按2.1.2方法计算。

2.3 双馈风机在PSS/E中的功率设置方法

表1为PSS/E33版本中风机无功功率控制方式[13-14]。本文在参考现有文献基础上总结归纳了双馈风机不同控制方式在PSS/E中的设置方法。

表1 PSS/E中风机无功功率控制方式Table 1 Control method of wind turbine’s reactive power in PSS/E

1) 恒电压控制方式。

风机节点应设置成PV节点，控制模式1与2都可用于模拟风机恒电压控制方式。

当不计及风机物理约束时可采用控制模式2。该模式下风机无功极限只由有功功率与功率因数决定。如双馈风机有功出力为0.9 MW，功率因数为0.98，则无功极限为[-0.18，0.18]Mvar。

为更好地模拟双馈风机的功率特性，当计及双馈风机的物理限制时，PSS/E33版本提供了控制模式1。在该模式下可通过计算得出双馈风机的功率极限，从而更好地模拟双馈风机的功率特性。

2)恒功率因数控制方式。

风机母线应设置成PQ节点，此时应选取控制模式3。输入对应的有功功率和功率因数即可。注意此处功率因数是由双馈风机与电网交换的功率确定的，而不是定子侧的功率因数。其等效功率因数为

(16)

2.4 PSS/E最优潮流功能的设置

PSS/E33版本中最优潮流功能的实现是以常规潮流计算结果为基础的，需要完成母线、变压器、发电机等元件节点命名、基准电压和功率、运行参数、上下限、分区及所属关系等信息的录入和编辑。

最优潮流数据对应 .opf文件，主要完成约束类型(强约束、软约束及软约束类型等)、权重等设置。在最优潮流求解界面中提供了5个标签，分别为目标函数、一般选项、误差、控制及报告。对于风机参数，在其优化界面中将选项无功功率的限制模式设置为out-of-service即可在潮流数据界面中按本文介绍的方法来设置其参数。

3 算例分析

选取内蒙古某60 MW风电场，风电场内有3条35 kV集电线路，3条集电线路分别有14、12及14台风电机组。为方便分析与说明，本文采用按升压站远近的原则进行编号，越靠近升压站的风电机组编号越小。本文算例中3条集电线路的风机编号范围依次为1—14、15—26、27—40。通过110 kV线路接入系统。升压站低压侧无功补偿容量[-0.78,15]Mvar。选取风速为10 m/s，恒功率因数控制方式，风机控制模式设置为控制模式3。常规潮流计算选取风机功率因数为1。风电场潮流优化控制变量选择双馈风机的无功出力、可投切电容器及有载调压变压器的变比。风电场接入系统节点设置为平衡节点[15]。

为验证PSS/E优化功能，选择以下3方面进行比较。从风机无功出力、节点电压、无功补偿量等方面比较各条件下潮流的分布规律。

1) 单目标最优潮流分析。

选取风电场有功损耗最小作为单一目标，为突出考虑最优潮流的作用，将常规潮流与最优潮流设置为无约束条件限制。通过仿真得如表2、图2所示的潮流结果及双馈风机的无功出力。

表2 最优潮流与常规潮流结果比较Table 2 Comparison of optimal trend and conventional trend results

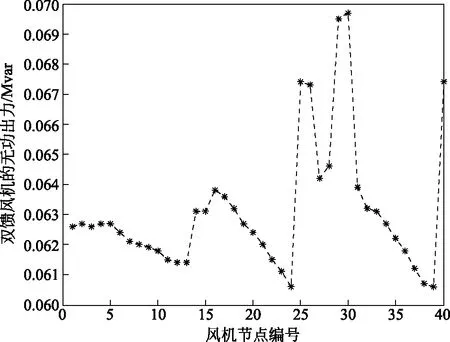
图2 无电压约束双馈风机的无功出力Fig.2 Reactive power of a non-voltage-constrained DFIG

由图2和表2可知：最优潮流下风电场有功损耗变小，各节点电压升高，风机输出无功功率。综合仿真结果可知，最优潮流中风机发出无功功率补偿集电线路与箱式变压器的无功损耗，减小了无功功率在风电场内部的流动，使风电场有功损耗变小。而系统作为平衡节点电压保持不变，风电机组作为供端向系统输送有功功率，所以供端与受端的电压降增大，从而使风电场的电压升高，而风电场电压的升高进一步降低了有功损耗。

2) 不等式约束与目标函数权重对最优潮流的影响。

最优潮流的计算过程实际上是各优化目标以及不等式约束互相博弈的过程，但在实际中有时可能会更加侧重某一目标或某一约束条件，这时侧重的部分应在寻优过程中占据相对主导地位。在PSS/E的最优求解过程中通过设置目标函数或约束条件的权重来调节相互之间的关系。表3为电压约束权重分别为10和1的潮流计算结果，图3为不同权重下的电压偏差。

表3 电压约束权重不同的最优潮流计算结果Table 3 Optimal power flow calculation results with different voltage constraint weights

图3 最优潮流不同权重各节点电压比较Fig.3 Comparison of voltages between nodes with different weights of optimal power flow

由表3可知，电压权重系数越大，风电场向系统输送的有功功率越小，这意味风电场总有功功率损耗增加。与电压权重为1相比，权重为10时电压偏差更小，说明此情况下在最优潮流的求解过程中电压约束变得更严格。

图4 双馈风机的无功出力Fig.4 Reactive power of DFIG

由图3可知，电压约束变得严格时，风电场整体电压偏差减小，而为不使电压偏差过大，如图4所示，部分双馈风机开始吸收无功功率，这样必然会导致有功损耗增大，此时为仍然满足整个风电场的无功需求，只能由无功补偿装置多发无功功率。

3) 复合优化目标的最优潮流计算分析。

本文结合现有文献选取有功损耗最小和无功补偿装置投资费用最小作为复合优化目标，且将两个优化设置为权重相同，即认为二者重要程度相同。为与有功功率损耗最小单一优化目标做对比，电压约束等权重取值均不改变，仿真结果如表4所示。

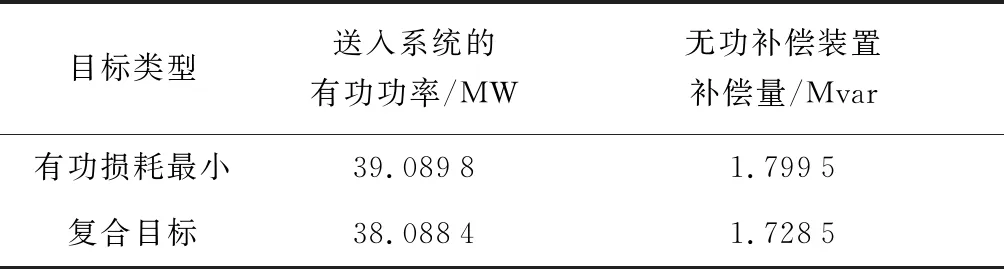
表4 不同目标函数潮流计算结果Table 4 Power flow calculation results for different objective functions

由表4可知：当采取以有功损耗最小为单一优化目标时，系统的功率损耗明显下降，但是需要无功补偿装置输出较多的无功功率；当采取复合目标时无功补偿容量下降，但是有功损耗增加，这体现了优化过程兼顾了两个优化目标。

4 结论

风能作为应用最广泛的新能源，其必将在电力系统中占有越来越重要的地位，优化风电场运行必将有利于风力发电的健康发展。本文主要分析了电力系统分析软件PSS/E中风机参数的设置方法及最优潮流功能的实现和分析。

1) 在现有文献基础上通过分析节点类型、双馈风机控制方式的特点，理清了风机在节点类型、控制方式及PSS/E设置参数之间的关系，明确了PSS/E软件中风机参数的设置方法。

2) 分析了PSS/E中内点法基本理论，得到PSS/E中最优潮流目标函数、约束条件、权重的处理方式及设置方法。

3) 借助于PSS/E分析软件分析了不同目标函数、不同约束条件对风电场优化的影响。仿真结果表明：权重越大的目标函数或约束条件在最优潮流求解过程中所占的分量越重，应尽可能首先满足；在最优潮流计算中要兼顾各优化目标与约束条件，权衡各目标或目标与约束条件之间的关系。