基于串并混联柔顺机构的三维力传感器设计
张 晨,张元开,王 均
(北方工业大学机械与材料工程学院,北京 100144)
0 引言
混联机构分为串并混联和并并混联两种,其中串并混联机构同时具备串联机构工作空间大和并联机构刚度高、承载能力大的优点,因而成为机构学研究的一个重要方向。柔顺机构是一种依靠自身弹性变形输出运动的装置,特别适合小变形领域,在一些需要小位移小转角的场合,柔顺机构可以达到很高的运动精度,且具有很多刚性机构不具备的优点。过约束并联机构,指多条支链对运动平台的约束之中存在重复约束的并联机构[1],常见平面连杆机构大多属于此机构[2]。
目前,常见的过约束柔顺并联机构多用于微动平台,本文将过约束柔顺机构反向应用的思路引入传感器的设计中,提出了一种基于串并混联柔顺机构的电阻应变式三维力传感器,用于小型扑翼飞行器空间力的测量,具有结构简单、精度高等优点。
1 三维力传感器构型设计
以柔性悬臂梁作为基本变形单元,传感器受力平台采用三分支平面并联过约束柔顺机构(3RRR机构)。三维力传感器弹性体由3部分组成:测量XOY平面力的上并联机构、测量Z方向力的下并联机构以及底座,如图1所示。其中,上并联机构由3-RR柔顺机构和3根敏感方向按XOY布置的悬臂梁(第1组)组成,这3根梁作为并联机构的驱动端(主动杆),动平台受的平面力将传递至第1组梁;用于测量Z方向力的下并联机构为受力方向按Z向布置的3根悬臂梁(第2组)。由于第2组梁的自由端与第1组梁的固定端连接,可视为首尾串联,也即上下并联机构的串联,由此构成的是串并混联机构。
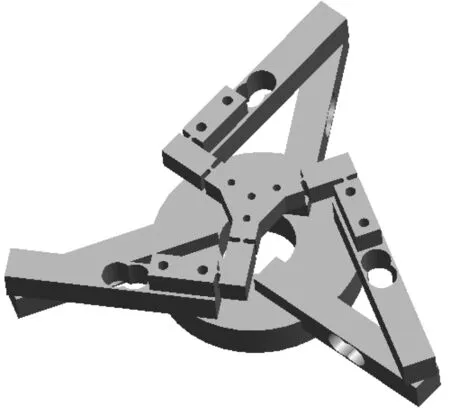
图1 弹性体三维模型图
2 运动学建模与MATLAB优化机构参数
2.1 运动学分析
由于本文研究对象应用场合为小变形领域,即在某位形下做微小运动,所以只需研究初始姿态(φ=0)下的位置分析,也称定姿态分析。如图2所示,以机构的几何中心O建立静坐标系XOY,运动平台中心OM建立动坐标系XMOMYM,两坐标原点初始位置重合,运动平台和静平台均为等边三角形。其中Ai(i=1,2,3)为主动关节,位置坐标为θi(i=1,2,3),主动杆AiBi=l;Bi(i=1,2,3)为中间关节,记从动杆BiCi=a(i=1,2,3),主从动杆的夹角αi(i=1,2,3);与动平台相连的关节记为Ci(i=1,2,3),动平台外接圆半径rM,结构分支对称布置,规定逆时针为正。

图2 运动学坐标系
根据以上规定,推导并联机构数学模型:(i=1,2,3)
(1)
其中(XAi,YAi)为驱动关节在参考系中的位置坐标;(X,Y)是运动平台中心在参考系中的坐标,φ为运动平台转角。
对式(1)两边同时求导,并整理形式为
(2)
则串并混联机构的运动学方程为
(3)
采用直接求解法得机构逆解:
(4)
由式(4)可知,机构共有8组逆解。考虑到运动连续性,得出一组合适的逆解如下:
2.2 MATLAB遗传算法工具箱优化参数
遗传算法是一种全局优化概率搜索算法,MATLAB遗传算法工具箱可提供一套对各种优化问题的解决方案[3]。本文基于雅可比矩阵,提出衡量机构运动学性能和力操作性能的灵活性指标[4](各向同性指标),即机构雅可比矩阵条件数。其中,机构处于某一位置的运动灵巧度由局部条件数cond(J)来衡量:

(5)
式中:σmax和σmin分别为雅克比矩阵J的最大和最小奇异值。
当条件数接近1时,机构具有良好的运动传递性能;当条件数趋于无穷大时,机构处于奇异位置。为了更全面地衡量机构的运动性能,根据给定工作空间来配置机构的有关参数,即工作空间的逆向分析[5],这对机构性能分析具有重要的意义。全局条件数定义如下:
(6)
式中S为已知工作空间。
优化模型如下:
(1)设计变量:x=[x1,x2]T(x1表示从动杆长度a、x2表示运动平台半径rM)
(2)目标函数:
minf(x)=|1-globalcond|
(3)约束条件(s.t.):
g1(x)=10-x1≤0
g2(x)=x1-30≤0
g3(x)=10-x2≤0
g4(x)=x2-50≤0
优化得到机构参数为a=15,rM=20。
3 静力学建模
虚功原理定义为受理想约束的力学系统处于平衡的充要条件是作用在系统上的所有主动力在任意虚位移下的虚功之和为零[6],利用虚功原理对混联机构进行静力学分析得到:
(7)

混联机构静力学方程如下:
(8)
对悬臂梁理论建模得到输入fn与输出ε之间的关系:
ε=4.670 7×10-6fn
(9)
由于X、Y两方向的力测量采用冗余敏感方式,根据静力学方程可知,fn2和fn3高度冗余,本文将fn3视为冗余力并剔除得到梁总应变与动平台受力之间的关系为
(10)
4 有限元仿真分析
本文使用的有限元软件为ABAQUS,主要利用有限元分析方法,对所设计的三维力传感器结构进行静态、模态以及刚度分析,从而验证结构设计的合理性。
4.1 静力分析
本文将应变最大值设为1.0×10-3并求出传感器
X/Y/Z方向的满载量程分别为±20 N/±20 N/±12 N。同时,εmax×E=72 MPa,小于硬铝合金屈服强度360 MPa,安全系数为5。在传感器3个方向满量程范围内分别施加多组力值,通过拟合得到3个方向的输入输出曲线,如图3~图5所示。

图3 施加X方向力时传感器的输入输出拟合直线

图4 施加Y方向力时传感器的输入输出拟合直线

图5 施加Z方向力时传感器的输入输出拟合直线
由图3~图5可知,本次设计的三维力传感器的3个测力方向线性度良好,说明弹性体结构的变形在线弹性变形范围内。
传感器3个方向上的灵敏度:
传感器3个方向上的耦合误差:
4.2 刚度分析
有限元法分析机构刚度已被较多研究者们采用,刚度反映位移与力之间的关系,本文通过刚度分析验证建模优化的正确性。
(11)
在动平台中心分别施加3个方向单位力得到3组位移值,则机构初始位置刚度矩阵如下:

结论:机构X、Y方向的性能基本一致,X/Y与Z方向的性能差别不大,总体机构各向同性良好,验证了优化的正确性。
4.3 模态分析
模态分析主要用于确定机构固有频率和振型,传感器前3阶固有频率、响应振型见表1。

表1 传感器前3阶固有频率、振型表
应变式力传感器属于低通型传感器,可由第1阶固有频率的2/3来确定其工作带宽,因此可以估算出该传感器的工作带宽为0~50 Hz,满足小型扑翼飞行器的应用要求(扑动频率在5~10 Hz之间)。
5 三维力传感器的静态特性测试实验
当输入量不随时间变化时得到的输出曲线为传感器的静态特性曲线。本文采用砝码加载方式,分别在X、Y、Z方向量程范围内取点施加回程力,采集数据并处理得到各自的输入输出曲线,如图6~图8所示。

图6 FX作用下的输入输出曲线

图7 FY作用下三维力传感器的输入输出曲线

图8 FZ作用下传感器的输入输出曲线
结论:传感器3个方向线性度良好,最大非线性误差均不超过0.1%;3个方向的灵敏度分别为0.227 3 mV/N、0.125 0 mV/N、0.100 7 mV/N;3个方向回程误差分别为0.03%、0.07%、0.21%。数据表明,本次设计的三维力传感器具有良好的静态性能,测试实验平台如图9所示。

图9 测试实验平台
6 结论
本文提出了一种柔性传感器弹性体,吸收了柔顺机构、混联机构以及过约束机构的优点,设计的传感器各项指标均满足要求。有限元仿真证明机构各向性能基本一致,线性度高,耦合度低,灵敏度高,回程误差小;此外,传感器工作带宽也满足小型扑翼飞行器的频率要求。

