基于用户特征和相似置信度的协同过滤算法
(河南理工大学 计算机科学与技术学院, 河南 焦作 454000)
网络的普及提高了人们的生活质量,每天在我们所生活的这个世界出现了大量的信息,信息的增长速度绝对是一件近乎恐怖的事情——我们称之为“信息爆炸”[1]。面对如此多的信息,较快地获取用户想要的或感兴趣的信息变得较为困难。推荐系统可以推荐给用户有用的信息,减少了用户获取信息的时间和精力。协同过滤推荐技术是在推荐系统中应用最早和最为成功的技术之一,因其可以充分利用信息间的联系,执行效率高,能够得到较好的推荐结果,因而成为当前研究的热点[2]。
协同过滤一般采用最近邻技术,利用用户的历史喜好信息计算用户之间的距离,再利用目标用户的最近邻居用户对商品评价的加权评价值来预测目标用户对特定商品的喜好程度,从而根据这一喜好程度来对目标用户进行推荐[3]。对于新用户而言是没有历史数据的,这就出现用户冷启动问题。针对此问题,魏琳东[4]等人采用了矩阵分解的方法和神经网络映射的知识各自对兴趣向量进行计算再融合。在现实生活中用户并不是对每一个项目都进行评分等行为,这就带来评分数据的稀疏性问题。针对此问题,王竹婷[5]等人用惩罚因子应对共同评分项较少的用户,并用依据自信息量所得的项目权值修正传统的相似度计算方法。
为了缓解算法存在的问题,本文提出一种基于用户特征和相似置信度的协同过滤算法(Attributes and Similar Confidence Collaborative Filtering,ASCCF)。将置信度和用户特征按比例引入到用户之间的相似性计算,得到较为可靠的用户最近邻居集合进而计算预测评分,并将评分从大到小的前N个推荐给用户。置信度可以避免两个用户共同评分项目很少时所带来的虚假相似现象,用户特征可以避免新用户因没有历史数据所造成的推荐质量较低的问题。
1 基础协同过滤算法
推荐算法一般包括三步:建立用户模型、寻找最近邻居和产生推荐[6]。
1.1 用户模型的建立
用户对项目的评分信息一般用R表示,R是一个m×n的矩阵。m表示用户的数量,n表示项目的数量,Rij表示用户i对项目j的评分。评分在[1~5]之间,用户的喜好程度与评分大小成正比。

表1 用户评分矩阵
1.2 寻找最近邻居集合
目标用户的最近邻居通过相似度计算来寻找,相似度越大说明两用户之间越相似。最常用的相似度计算方法有皮尔逊(Pearson)相关系数、余弦(Cosine)相似度和修正的余弦(Adjust Cosine)相似度[7]。
(1) 皮尔逊(Pearson)相关系数:首先会找出两位用户都曾评论过的项目,然后计算两者的评分总和与平方和,并求得评分的乘积之和。
(1)

(2) 余弦(Cosine)相似度:用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
(2)
式中,rai、rbi分别为用户a和用户b对项目i的打分;simcos(a,b)为两用户的余弦相似度。
(3) 修正的余弦(Adjust Cosine)相似度:考虑到每个用户打分时都打分习惯的影响,经用户的评分去掉用户的平均评分来均衡用户的评分差异。
(3)
式中,rbi为用户b在项目i上评论分数;Ia、Ib分别为两用户各自评论的项目集合;sima-cos(a,b)为用户间调整的余弦相关性。
1.3 产生推荐
用以上任一种相似度计算方法进行计算,获取最近邻居集合之后,利用式(4)对用户没有打分的项目进行预测打分,并将预测分数从大到小取前N个推荐给目标用户。
(4)
式中,Ua为目标用户a的最近邻居集合;sim(a,b)为皮尔逊相关系数;prea,i为目标用户a对没有打分的任一项目i的预测打分。
2 算法改进
2.1 基于置信度的相似度计算
并不是用户对所有的项目都进行评分,由于不同用户的不同的兴趣爱好,所以用户的打分项目各种各样,所得到的用户评分矩阵稀疏度很大。在获取用户最近邻居集合的时候,无法反映用户的相似喜好,尤其是两个用户共同评价的项目只有一个的情况下,他们的相似度很高[8]。
因此,在计算用户相似度时需要有一个置信度,本文将Jaccard函数[9]作为置信度的度量函数,公式如下:
(5)
式中,I(a)、I(b)分别为用户a和用户b各自打分的项目集合;|I(a)∩I(b)|为两用户打分项目的交集数量;|I(a)∪I(b)|为两用户打分项目的总数量。
将式(5)引入到相似性计算公式(1)中,得到一个改进的相似性度量公式,如下:
(6)
式中,S(a,b)为相似置信度。simi(a,b)在一定程度上缓解了两用户共同打分项目少时造成的相似虚假现象,提高了推荐的质量。
2.2 基于用户特征的相似度计算
用户一般拥有用户编号、年龄、性别、职业、邮编等基本的信息。这些基本特征在一定程度上会影响着用户的兴趣喜好,拥有相同特征的用户可能会是相似用户。这些信息可以分为三类:① 年龄;② 性别;③ 职业和邮编。在新用户来临没有历史数据的情况下,用户特征显得尤为重要,所以将用户的基本特征引入到相似度的计算中,可以避免用户冷启动所带来的推荐效果不好的问题。
(1) 用户年龄特征。不同年龄的人喜好会有所不同,比如儿童喜欢动画片,少年喜欢青春偶像剧,老年人喜欢经典影视。两用户的年龄差距越小,其喜好相似性越大,超出一定范围时相似度受年龄的影响微弱。本文中将这一范围定为10,年龄特征的相似度计算如下:
(7)
式中,UAa、UAb分别为目标用户a和相似用户b各自的年龄;simage(a,b)为两用户的年龄相似度。
(2) 用户性别特征。性别相同的用户喜好一般会相同,如女性比较喜欢化妆品,男性比较喜欢汽车等。性别的取值只有两个,所以性别特征的相似计算公式如下:
(8)
式中,Sa、Sb分别为用户a和用户b各自的性别;simsex(a,b)为用户间性别的相似度。
(3) 用户标称特征。有相同职业的人可能有相同的喜好,如学生常看书籍,医生常看病例等;有相同邮编的人说明所处地区相同,他们可能会对该区域内的一些东西感兴趣。对用户的标称特征的相似计算公式如下:
(9)
式中,n为两用户间相同标称特征的数量;m为用户标称特征的总数量;simother(a,b)为标称特征的相似程度。
通过上述所得的各种特征的相似性可以用公式(10)计算用户a和用户b在用户特征上的整体相似度。
(10)
式中,c为用户特征的分类数;sima(a,b)为用户特征的整体相似度。本文按用户各类特征所占比例相同计算。
2.3 基于最终相似度的推荐
改进的相似度计算能够应对数据稀疏性和用户冷启动,把基于用户特征的相似计算公式与基于置信度的相似计算公式进行结合:先计算基于用户特征的相似度;再计算基于置信度的相似度;最后将单独计算所得的两个相似度按照前者w的比重,后者(1-w)的比重进行相加得到最终的相似度。相似计算公式如下:
Fsim(a,b)=wsima(a,b)+(1-w)simi(a,b)
(11)
式中,Fsim(a,b)为用户的整体相似度。整体相似度越高,说明两用户越相似,喜好也越接近,推荐给目标用户的结果也更符合用户的需求。
2.4 改进的算法描述
Input:用户评分矩阵Rm×n,用户特征信息,最近邻居数K,目标用户a。
Output:目标用户a的Top-N推荐集。
① 将用户评分信息转化为用户评分矩阵Rm×n,利用式(6)计算用户间的相似程度,获得simi;
② 利用用户特征信息,获取用户的各类特征,并分别计算用户间的年龄相似程度simage,性别相似性simsex,标称特征相似程度simother;
③ 将所得的各类特征相似程度代入到式(10)中,从而获得用户特征的整体相似程度sima;
④ 把第①步所得的结果和第③步所得结果利用式(11)进行计算,取得最终用户相似度,并得到目标用户a的最近邻居集合Ua;
⑤ 根据目标用户a的最近邻居集合Ua和式(4)对未打分的项目进行预测打分,对分数从大到小排序,形成Top-N集合进行推荐。
2.5 算法分析
本文的相似度算法与传统的相似度算法(余弦相似度)复杂度都为O(n2)。本文中每两个用户特征总相似度计算需2次加法,一次除法,开销很小;计算置信度相似度计算时,在Pearson相关系数计算公式之后乘以一个置信度。而文献[5]在计算相似度时,在Pearson相关系数计算公式中为每个项目增加权值。两相比较知本文算法的开销小于文献[5]中算法的开销。
3 实验结果及分析
3.1 实验数据
实验选取的MovieLens数据集,是由GroupLens研究小组在明尼苏达大学研究项目上收集的。其中包括943个用户对1682部电影的100000条评分记录[10]。用户的打分最低为1,最高为5,所打的分数与用户的喜欢程度成正比。根据数据稀疏性公式可以计算该数据集的数据稀疏度[11]。
(12)
式中,Spa为数据集的稀疏程度;num为打分总数量;m为用户的数量;n为项目的数量。用式(12)计算得到该数据集的稀疏程度为93.69%。
3.2 评测标准
推荐系统准确性测量分为3类:预测准确测量(如MAE、RMSE)、分类准确测量(如ROC曲线)和排序准确测量[12]。本文采用平均绝对误差(Mean Absolute Error,MAE)作为度量标准,MAE的定义如下[13]
(13)

3.3 实验结果分析
在数据集中给出了5个训练集(u1.base,u2.base,u3.base,u4.base,u5.base)和5个测试集(u1.test,u2.test,u3.test,u4.test,u5.test)。随机选取一个训练集和与其相对应的测试集进行实验。
改进的相似度计算是由基于置信度的相似计算公式与基于用户特征的相似计算公式用一个因子w进行结合得到的。对于新用户而言,没有历史数据作为推荐的依据,此时用户的特征起到主要作用;对于老用户而言,大量的历史数据可以为用户提供充足的依据,此时用户的特征作用会有所减小,所以理论上w取值在0~0.5之间。下面由实验进一步来确定w的最佳取值。
w的值从0开始取间隔为0.1,到1为止,w=0表示相似性计算公式中只有置信度,w=1表示相似性计算公式中只有用户特征,不同w的取值所得的MAE值结果如图1所示。从图1可以看出w在取0.1时,MAE取值最小,算法效果最好。

图1 不同w的取值与所得MAE
目标用户的最近邻居数的不同取值对MAE也有一定的影响,最近邻居数越小,用户冷启动的可能性越大。利用上述实验所得结果,将w的值定为0.1,最近邻居数从10开始间隔为10直到100为止,计算不同邻居数下的MAE值大小,结果如图2所示。从图2中可以知道用户最近邻居数最小时MAE取值最小,这就说明改进的协同过滤算法的推荐质量在用户冷启动时有所提高。
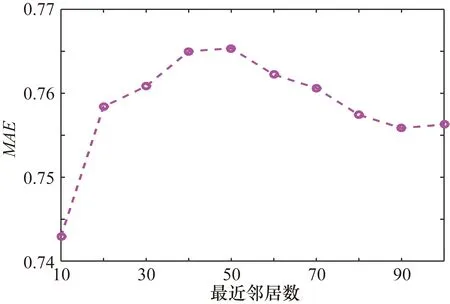
图2 不同最近邻居数下的MAE取值
为更好地体现改进的协同过滤算法的效果,将本文的改进算法(ASCCF)与传统的协同过滤算法(修正余弦相似度)和文献[5]的改进算法相比较。用户最近邻居数从10开始间隔为10依次增加到100 为止,比较不同邻居数量下各自算法的MAE取值。所得的实验结果如图3所示。从图3可知,最近邻居很少时本文的算法结果最好,随着最近邻居数量的增加,本文改进的协同过滤算法所得的MAE值虽然有所增大,在70点处与文献[5]相同,80点处比文献[5]好,最近邻居数大于85时稍逊色与文献[5],但依然比传统算法的MAE值小,所以本文改进的算法更适用于最近邻居数小的情况。

图3 3种方法的比较
4 结束语
本文针对算法中存在的数据稀疏和用户冷启动问题,对最初的传统过滤算法进行改进,提出一种基于用户特征与相似置信度的协同过滤算法。置信度的引入让两用户在共有打分项目较少情况下,减少了两用户间相似的假象,用户相似度得到保证进而提高了推荐的准确性。用户特征的加入,让新用户通过自身特征计算用户间的相似程度,避免了冷启动所带来的困扰,进而保证了推荐的质量。再用一个因子将两种相似度计算方法联系起来,控制各自所占比重计算用户间最终相似程度,获取目标用户的K个最近邻居集进行预测打分,按照打分的高低形成Top-N推荐给目标用户。实验表明,在评分矩阵稀疏和冷启动的情况下,本文改进的算法效果很好。但没有考虑用户的兴趣会随时间的变迁而发生变化,在最近邻居数越大的情况下算法也有待改进,因此考虑用户兴趣的时间有效性和在较大最近邻居数下提高推荐质量将是本文的下一步研究。

