基于学习目标导引的教学问题设计
杨小兵 易良斌


摘要:教学中落实好数学学科核心素养的关键是教师要结合相应的教学内容,在落实“四基”、培养“四能”的过程中,在基于学情的“问题组”引领下,推进学生积极的深度思维,促进学生数学学科核心素养的形成和发展。
关键词:学习目标;问题;设计
如何才能在教学中落实好数学学科核心素养呢?章建跃博士认为其中的关键是要结合相应的教学内容,在落实“四基”、培养“四能”的过程中,促进学生形成、发展数学学科核心素养。教师要把握好教学内容的整体性、系统性和完整性,以研究一个数学对象的“基本套路”为依据,以“教学主线”强化内容。教师应该通过“概念(内涵)—性质(关系)—结构(联系)—应用”这一过程反映的数学教学思想方法,显化“事实—方法—方法论—数学学科本质观”的数学育人过程,把数学学科核心素养落实到位。
崔允漷教授认为教学变革要从教案开始,教案不变,课堂就不会变。教学设计即教学方案应该是教师开给学生的学习“处方”,让学生明白去哪里、怎么去、怎么知道已经到那里了,即教师不要整天只关注自己怎么教,而要关注学生学会什么、有没有学会、怎么学会的。
一、学习目标定位
《义务教育数学课程标准》对“变量与函数”的教学目标设计为:“探索简单实例中的数量关系和变化规律,了解常量、变量的意义;结合实例,了解函数的概念和三种表示法,能举出函数的实例;能结合图像对简单实际问题中的函数关系进行分析;能确定简单实际问题中函数自变量的取值范围,并会求出函数值;能用适当的函数表示法刻画简单实际问题中变量之间的关系;结合对函数关系的分析,能对变量的变化情况进行初步讨论。”
我们针对官方设定的教学目标中的关键词进行了分析。“探索”属于过程性目标。探索规律是想通过探索得到规律,转换成认知目标应该是“推断”。“了解常量、变量的意义”旨在让学生通过实际例子归纳、总结,能举例说明常量、变量的意义。结合实例了解函数的概念,是“总结”。要了解三种表示法,那就需要对三种表示法进行“比较”,能举出函数实例,这就要求学生能够“举例说明”“解释”。结合图象对实际问题中的函数关系的分析是“解释”。确定简单函数自变量的取值范围是一种方法,要让学生领悟这种方法,关键也在于教师对这种方法的“解释”。“能确定……”则是对方法的执行。
我们觉得官方给定的目标比较散乱,且与学情不符。我们经过研究讨论,将教学目标重新定位为以下方面。(1)知识技能:了解“常量”与“变量”的含义,能分辨实例中的常量与变量;在丰富的现实情境中领悟“函数”的概念,掌握函数的三种表示方法。(2)数学思考:经历常量与变量、函数的探索与抽象概括过程,感受数学建模思想和“变化”与“对应”的数学观念。(3)问题解决:通过观察几个具体实例里的数值变化与变量之间的关系,归纳出“变量”与“常量”的定义,及“函数”的概念,以此锻炼学生的抽象思维能力和分析问题能力。(4)情感态度:让学生经历在现实情境下对“变量”“常量”以及“函数”概念的抽象过程,从而感受数学在生活中的应用价值,培养起对数学的研究兴趣,感受成功探索发现的喜悦感。
二、课堂情境再现
师:我从杭州到安徽来和大家一起学习“19.1.1变量与函数”,你认为老师出发前要做哪些准备?
生:(七嘴八舌)课件、习题、火车票…
师:我若开车,以80km/h的速度匀速行驶,情形会是什么样的?请看大屏幕。
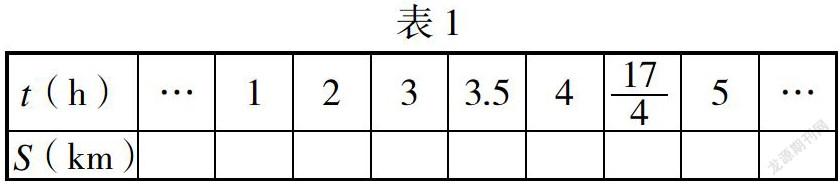
1.汽车若以80km/h的速度匀速行驶,行驶路程为Skm,行驶时间为t h.
问题1:填表。
问题2:请你选择一个时间点,算出那时的行驶路程。
问题3:从上述过程中,你感受到了哪些“变与不变”的量?
问题4:请你用一句话来描述变量t和S之间的联系。
问题5:请你用一个式子来表示变量t和S之间的联系。
问题6:汽车若以akm/h的速度匀速行驶,行驶路程为Skm,行驶时间为t h。在这个过程中,变量和常量又是哪些?
[设计意图]让学生通过问题情境体验生活中的变与不变,之后经历“代一代”的方式,明白:每确定一个时间t,行驶路程S总是唯一确定的。杨老师通过问题串的设计,启发学生思考;从数到字母的层层递进,让学生经历从特殊到一般的过程,促进了其脑海中“变量”与“常量”概念的形成,引导学生从具体情境中抽象出数学概念。
师:“在路上”,我们感受到了黄山风景的优美!请接着看题——
2.我们了解到2008年以来黄山旅游人数如下表:
問题1:在这个过程中,变量和常量是哪些?它们之间的联系是怎样的?
问题2:现在可以知道2019年的旅游人数吗?(追问:从表格中看得出吗?现在求出的最终答案会是唯一的、确定的吗?)
[设计意图]杨老师通过问题情境,让学生体验列表中的变与不变,并让学生通过“查一查”的方式,明白:每确定一个年份,旅游人数总是唯一的、确定的。2018年黄山旅游人数是多少?现在统计结果还没有出来,但最终结果必然是唯一的、确定的。之后,让学生讨论“现在可以知道2019年的旅游人数吗?”并着重强调“现在”,将关于函数模型下的现实数据是否“唯一、确定”的讨论推向高潮。
3.师:老师上完课就回去了,你们要是喜欢老师,要常给我写信啊!在国内,投寄平信应付邮资如下表:
问题1:四名同学的四封信件质量分别为5克、20克、40克和50克,则他们分别付邮资多少元?
问题2:y是m的函数吗?
[设计意图]从“出发前”的准备,到“在路上”的所见所感,再到“在课堂”的精彩表现,最后到离别前的“再联系”——杨老师从现实生活中的此情此景入手,顺势激发学生对邮寄信件知识理解的愿望;更是进一步辨析、凸显函数概念的重要性,让学生明白函数的初始本质是“多对一的唯一确定形式”,凸显生活与数学的联系。
三、课后教学反思
(一)激活学生深度思维,营造民主、平等、和谐的课堂教学氛围是前提
一位老师在听课心得里这样写道:“会聊天的老师受欢迎”。杨老师先从他们一行人为何从杭州来到祁门、来前要做哪些准备开场,将“出发前——在路上——在课堂——再联系”的整个过程娓娓道来,课就这样展开了。无论是陌生的老师,还是熟悉的老师,会聊天的老师显然更容易拉近与学生的心理距离。聊的可以是老师的事,也可以是学生的事,关键在于聊天中要蕴含着可用于本课学习的经典例子。教师只有真正做到营造民主、平等、和谐的课堂学习氛围,才能唤醒学生积极思考的愿望,激活学生的深度思维,如此,课堂教学才会更有效、更精彩。
(二)激活学生深度思维,有效诱思、有效引导的问题组设计是关键
教学是教师引起、维持或促进学生学习的所有行为。教学的本质不是师生互动,也不是我启你发,而是你学我帮。学生学习的关键在于思考(肯思考、会思考)。教师的主要任务是启发学生思考。而能够推动学生思考的肯定是一些具体的任务。数学课堂要从“对话中心”转向“任务中心”,以任务驱动引发学生的思考。教师应该通过“趣问题组”启发学生的思维,“近问题组”迁移学生的思维,“动问题组”联结学生的思维,“深问题组”转化学生的思维,从而达到激活学生深度思维的目的。
(三)激活学生深度思维,及时的评价和鼓励是催化剂
一位老师在听课心得里这样写道:“当学生回答得好时,及时的掌声与表扬,可以让学生保持较为持续的积极性。”当然,鼓励的方式可以多样些。鼓励不仅应在学生完成任务时出现,当学生面对困难产生小小的畏难情绪时,一点鼓励就可能让他突破自我。在课堂上,有一个小细节,当一位女生回答得非常好时,杨老师主动、认真地问清她的姓名。远道而来的名师采用的这种交流方式让学生幸福感满满。杨老师还总是在课堂上有意或无意地留给学生“接嘴”的机会。如果是有意的,则是杨老师精心设计课堂的体现,给了学生勇敢表现的机会;如果是无意的,那就是有感而发的主动亲近。这一切都体现了杨老师是多么善于发掘学生的生成性资源,更体现了杨老师身体力行地践行着“以生为本”的理念。
参考文献:
[1]易良斌.中学数学教与学[M].北京:光明日报出版社,2015.
[2]史寧中.义务教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版社,2018.
(责任编辑:韩晓洁)

