基于集成学习的武汉二手房估价模型研究

姚冲　闭鑫业

摘要：本文通过集成学习方法对武汉市二手房的数据进行分析和研究。本文构建了三种二手房房价估值模型：一、决策树集成的随机森林模型：二、通过AdaBoost，采用多层感知器神经网络构建了神经网络集成模型;三、用XGBoost方法建模，并对三种模型进行分析对比，结果显示使用AdaBoost算法建立的模型更准确。

关键词：武汉二手房：集成学习：随机森林：XCBoost

随着全国二手房关注度的提高，与二手房交易相关的抵押等交易越来越丰富，而买卖前的二手房估价是非常重要的环节。现有运用数理模型进行房价预估的研究中较为常见的是采用最小二乘法拟合多元线性回归法。这种方法在建模的中一般要求误差项要符合零均值并且独立同分布的设想。此外，这些方法通常用t检验来检测回归系数的显著性，用F检验来检测模型整体水平的显著性。但是如果数据不能够满足正态性条件，t检验与F检验的方法相对不满足正态分布的数据来说没有多大意义。在对相对复杂的数据进行建模时，简单的线性回归算法会有欠拟合和模型解释能力较低的问题。为了避免以上评估方法的限制，寻找到更好的评估方法，本文使用集成学习的方法，用随机森林、AdaBoost、XGBoost三种方法进行建模，分别得到随机森林、AdaBoost、XGBoost三个模型，用测试集数据进行测试，再进行调参，用MAE（平均绝对误差）评估模型的适用程度。

一、数据探索

（一）数据来源

1.原始数据

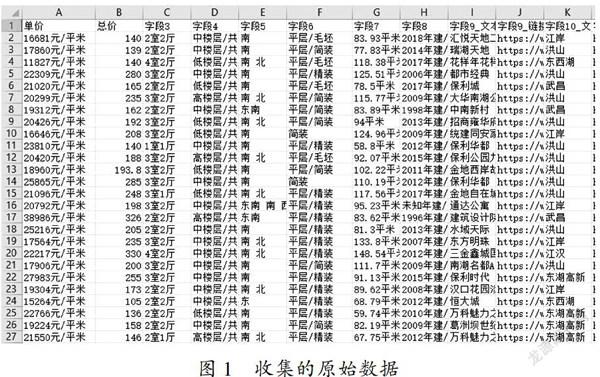
本次报告所采用的数据源来自“链家网”中的武汉二手房相关数据f如图l所示 2.数据清洗 如图l所示，数据不仅结构混乱，且含有缺失值，不匹配的记录。首先，删去不匹配的、缺失值内容太多的记录：其次，利用Python将混合字段拆分成独立的字段;最后，利用替换功能，将特殊字符、单位去掉变为数值型数据，并将变量的数据统一化处理。经过处理后，研究的变量为武汉二手房每平方米的价格，影响因素包括武汉二手房的建房年份、面积、楼层位置、楼层總高度、卧室数量、所在区域、装修情况、户型结构、产权年限、是否配备电梯等因素。

（二）描述性分析

1.武汉市二手房房价分布

根据上述处理过的数据，利用Pvthon绘图工具包mat-plotlib和seahorn分析工具可得出二手房单位价格大多处于10000 - 30000元之间，且集中在50平方米至150平方米区间内，分布带有轻微的有偏性，但大致服从正态分布，高价位和低价位的二手房数都相对较少，且最高不超过5万/平方米。

二手房相对于新的商品住宅来说，楼房建造时间对价格影响较大，武汉市二手房建造年份主要是在2000年左右，相对较新：而2000年之前的老房子挂牌销售的较少。

2.武汉市二手房房价影响因素分析

对二手房房价影响的因素有很多，如楼房是否有电梯，房子所在区域，楼层结构，产权年限以及装修程度等因素。

首先，影响价格因素最大的是区域。武汉市在售的二手房在洪山区、武昌区、江岸区等区域的房价较高，而蔡甸、新洲地区房价相对较低。

其次，武汉市在售的二手房中影响次要原由楼层结构，装修程度等。在售房中，主要楼层结构有平层、复式、错层、跃层，其中复式价格相对较高，而平层是购房较多的购房结构。产权年限对价格的影响也比较大，一般选择70年产权比较符合大多数人的情况。装修方式对房价的影响也比较显著，其中精装的武汉二手房房价相对较高，其余装修方式对应的房价依次按照简装、毛坯的顺序递减。

最后，电梯对二手房价格有较明显的影响，有电梯的二手房房价集中偏高于20000元每平方米，而没有电梯的二手房房价则明显低于有电梯的。

综上所述，最受关注的武汉二手房，其每平方米的价格大概是20000元左右，面积普遍都在50平方米至200平方米之间，高楼层，楼型为板楼，建筑时问在2000年以后。并且，处于武昌、江汉区等繁华地区、装修方式为精装、楼型为板塔结合、社区有电梯的二手房房价相对较高。

二、武汉市二手房建模及评估

（一）建模流程

1.建模思路

经过数据清洗后，将清洗后的数据分为训练集、测试集，分别为变量训练集X_train、变量测试集X test、因变量训练集y_train、因变量测试集y_test，分别得到以随机森林、AdaBoost、XGBoost为算法的模型，进行调参，选取最好的结果，对这三个模型进行比较，选中较好的模型作为预测模型。

2.基础算法与集成算法

本文对数据进行集成算法训练前也对基础算法进行训练，有线性回归、逻辑回归、决策树回归等，对其进行建模，得到的MAE远大于集成学习的评估，对此基础算法对于该数据的二手房估价并不是很准确，因此选择了集成学习算法进行构建估价模型。

（二）随机森林

利用Python软件中的sklearn库的随机森林算法，通过调节算法中的超参数，让模型达到最好的拟合效果。其中，需要调节的主要参数。

n_estimators是指随机森林算法中决策树的数量，默认值为10，经过不断调试，n_estimators= 250时，MAE达到较好的效果。

n_johs= -1为计算机使用最大核数，只影响计算时间，不影响计算结果。

random_state为随机种子，这里的参数值为666，为了方便对比，不会因为训练集所选的数据不一样影响结果。

max_samplessplit=4，所需的最少样本数量作为分割内部节点，经调试，等于4时效果最好。

max_depth= 45，树的最大深度，防止过拟合，该超参数力45时效果最好。

经过调节这些参数后计算出MAE= 2563.3151。

f三）AdaBoost

同样的在Python中的sklearn中使用AdaBoost算法，其调整的参数类似与随机森林，因为两种算法都是以决策树为基础，参数意义基本相同。需要调节的主要参数。

maxdepth= 15，樹的深度，防止过拟合，在此算法中，该超参数为15时效果最好。

maxsamples_split=4，参数意义同随机森林。

random_state= 666，参数意义同随机森林。

n_estimators参数意义同随机森林，默认值为10，经过不断调试，n estimators= 480时，MAE达到较好的效果。

最后输出的MAE= 2524.6871。

（四）XC.Boost

在Python中，使用XCBoost建模，其主要超参数。

min_child_weight是最小叶子节点样本的权重和。xc-Boost是这个参数是最小样本权重的和，而CBM是最小样本和，这个参数用于避免过拟合。min_childweight=6时MAE达到较好的效果。

gamma是算法在节点分裂的时候，当分裂后损失函数的值下降了，才能分裂这个节点。Gamma指出节点分裂所用最小损失函数下降值。这个参数越大，算法相对保守。Gamma=0.1，效果最好。

colsample_bylevel用来控制决策树的每级的每次分裂，对列数特征的采样的占比，colsample_bylevel=0.9时效果较好。

lamhda权重的L2正则化项（Ridge regression类似）。参数是用来控制XCBoost的正则化部分，防止过拟合，lamhda=l时效果较好。

最后输出MAE= 2861.4871。

（五）模型评估

在使用集成学习算法构建成的模型，使用随机森林建立起的模型进行估价，将会存在2563元左右的误差，使用AdaBoost算法建立的模型，对该二手房数据的拟合更高，得到更好的估价模型。

经过调试三个模型，AdaBoost的模型效果比随机森林和XCBoost更好，相对于武汉市二手房均价20000元/平方米的价格，AdaBoost的模型预测误差MAE在2500元左右，是均价的12.6%左右，该模型可以对武汉市二手房做大致的估价（如表2所示）。

三、结果与展望

（一）分析总结

本文通过对从链家网获取的2985条武汉市二手房交易数据进行探索、集成学习的方式建立估价模型，得到以下结论。

第一，从变量来看，房子的区域、大小、建造年份对价格影响比较大。武昌、江汉等区域二手房房价相对较高，江夏、蔡甸等区域则相反：房价每平方米的价格大概是20000元左右，面积普遍都在200平方米以下，位于高楼层，楼型为板楼，社区有电梯、建筑时问在2000年以后等特点。

第二，对于二手房价格估价模型，集成学习优势高于单个算法建立的模型，在随机森林、AdaBoost、XCBoost这三个模型中，AdaBoost拟合效果最好，能更好地对二手房进行估价。

第三，在房地产估价中，人T-智能以及机器学习的介入，可以帮助该行业迅速发展。当二手房中介建立估价模型时，应当使用大量二手房交易数据，信息越详细通过机器学习训练出来的模型，才能更准确地对房价进行估算。

（二）研究的不足与展望

本文不足主要在数据获取方面，首先，因为计算机性能、软件、二手房网站信息不全等方面的影响，收集到的数据较少，缺失较大，信息不详细，用于建模的数据噪音较大，以至于影响最后结果。其次，没有在文本挖掘方面提取其他信息，比如是否靠近地铁，是否是学区房等因素。最后，二手房市场的价格容易受政策的干预，应该进一步考虑到政策的影响。

参考文献：

[1]吴姗撕.基于BP神经网络的南京市房价预测[J].市场周刊.2016.

[2]袁秀芳，郑伯川，焦伟超.基于SVR的上海市商品房价格预测『J].西华师范大学，2016.

[3]霍妹宇，王春萍，史朝阳.基于聚类分析技术的昆明二手房源价格分析[J].中国集体经济，2016.

[4]王智超.基于数据挖掘的房价预测分析[J].四川大学.2017.

[5]刘冰，金跃强，王书营.南京市二手房房价影响因素的多元线性回归分析[J].南京工业技术学院，2017.