基于网络层次拓扑结构的公路网多目标最优路径算法
龙威栋



摘要:公路网多目标最优路径问题(Multi-objective Optimal Path Problem of Highway Net-work,MOPPHN)是一个活跃的研究领域,因为它应用于大量系统。在路网系统中,有必要找到从一个节点到指定节点或所有其他节点的最佳路径。在最坏的情况下,用于计算从指定源节点到MOPPHN中所有其他节点的所有多目标最优路径的计算复杂度是指数级的。文章提出了一种算法,用于在网络层次拓扑结构内找到一组多目标最优路径的值,而不是在指数时间内生成多目标最优路径的所有值,这在许多情况下都是非常重要的。应用文章提出的算法,可以找到网络中任何MOPPHN的一组多目标最优路径,即使它包含负循环。通过实验分析,验证了该算法在实际和理论上都表现良好。
关键词:网络;多重目标;多目标最优路径
中图分类号:U491 文献标识码:A DOI:10.13282/j.cnki.wccst.2019.10.048
文章编号:1673-4874(2019)10-0174-05
0引言
网络优化问题是运筹学和管理科学中研究最多的课题之一。网络模型可以从大量应用领域获得,例如运输系统、通信系统、电力传输系统及水、血液、气体和排水的管道分配系统,神经决策系统、生产计划和项目规划等。这种网络中涉及的目标数量可以是一个或多个。这里的基本问题是找到从特定起始节点到所有其他节点的最佳路径或帕累托最优路径。在单目标最短路径问题(SOSPP)中,只考虑一个目标,而公路网多目标最优路径问题(MOPPHN)由多个目标组成。对于SOSPP,文献中存在许多有效的算法以找到从一个节点到另一个节点或从一个节点到所有其他节点的最短路径。万莹等对运输网络的多目标设计和42个选定参考文献的注释书目进行分类,提交了一份关于MOPPHN的调查报告。一个特定的网络证明了在最坏情况下生成所有Pareto最优解使两个目标最短路径问题变得难以处理,因为公路网多目标最优路径的数量随着节点数量呈指数增长。网络中任何MOPPHN的公路网多目标最优路径的最大数量,在最坏的情况下,是1+(n-2)+(n-2)(n-3)+…+(n-2)!+(n-2)!它位于2[(n-2)!]和3[(n-2)!]之间。有研究提出了MOPPHN的标记算法并修改了Hansen网络,表明标记算法还可以确定指数数量的主导标签来计算单个最优解,给出了一种使用动态规划方法解决MOPPHN的算法,这在理论上也不是一个好的算法。
因此,用于生成从源节点到MOPPHN中的所有其他节点的多目标最优路径的所有值的现有算法都是指数时间算法。这促使本文研究网络层次拓扑结构以多目标最优路径的值集的子集来改善时间复杂度。本文提出了一种顾及网络层次拓扑结构的公路网多目标最优路径算法,该算法通过确定相应SOSPP的第一个多目标最优路径,生成网络中MOPPHN的多目标最优路径的所有值集合的子集。首先使用算术平均技术确定对应于网络的给定MOPPHN的SOSPP。如果网络的MOPPHN具有负循环,则所有现有算法仅指示负循环的存在,即指数操作之后也是如此。但是,应用本文提出的算法,可以找到网络中任何MOPPHN的一组多目标最优路径,即使它包含负循环。
1基本知识
1.1 符号
1.2 相关知识
1.2.1 网络
1.2.2 路径和无环路径
V的节点i和j之间的路径是连接节点i和j的连续边缘序列,本文还可以通过其节点的序列(v,…,v)来表示路径。如果路径的节点序列是有限的,那么该路径被认为是有限的。如果网络的所有节点都是不同的,则称其为无环路径。
1.2.3 路径的值
1.2.4 多目标最优路径问题
2 多目标最优路径算法
本文提出的算法需要计算多目标最优路径。基本标签校正算法用于找到多目标最优路径。基本标签校正算法仅生成不包含负循环的网络的多目标最优路径的值。生成的值对应的多目标最优路径可以包含循环。本文已经包含了一个额外的步骤,它跟踪无环路径并生成非减少k最短无环路径和路径本身的值。由于算法生成无环路径,因此它可以应用于任何网络,即使它包含负循环。为了确定无环路径,该算法需要额外的O(nk)基本操作。因此,确定k-最短无环路径的最坏情况计算复杂度是。(nkIogn+nk),该算法将给定的网络MOPPHN转换为SOSPP。通过用相应边缘的矢量权重的分量的算术平均值替换网络的每个边缘的矢量权重来完成变换。它确定SOSPP的第一个多目标最优路径,并且从这些路径确定给定MOPPHN的多目标最优路径的子集。
步骤2:将任何多目标最优路径算法应用于简化的SOSPP,以找到从给定源节点到网络的每个其他节点的第一个多目标最优路径P(i=1到k)。
步骤3:对于每个路径P,通过添加构成路径P的边的矢量权重来确定网络的MOPPHN的值MP。
步骤4:求MP=Pmin{MP,MP,…,MP},其中MP(i=1至k)是第j个最短路径P的矢量权重。
为了找到第一个k-最短无环路径,所提算法的步骤2需要O(nklogn+nk)基本運算,其中n是节点数,k是所需的最短路径数。为了确定k组值的Poreto最小值,步骤4需要O(k)个基本运算。该算法所需的基本运算总数为O(nklogn+nk)+O(k)=O(nklogn+nk)。
由于多目标最优路径的值是通过对位于路径上的边的所有矢量权重求和而获得的,因此不能应用所有其他平均值,如几何和调和平均值。考虑路径(v,v,v),其边缘(v,v)和(v,v)的矢量权重分别为(a、,a,…,a)和(b,b,…,b)。现在,边缘(v,v)和(v,v)的矢量权重分量的几何平均值是(a×a× …×a)和(b×b×…×b),路径的值是:
(a×a×…×a)+(b×b×…×b)
(1)
路径的矢量权重是[(a+b),(a+b),…,(a+b)]。
路径的值等于路径的矢量权重的分量的几何平均值
[(a+b),(a+b),…,(a+b)] (2)
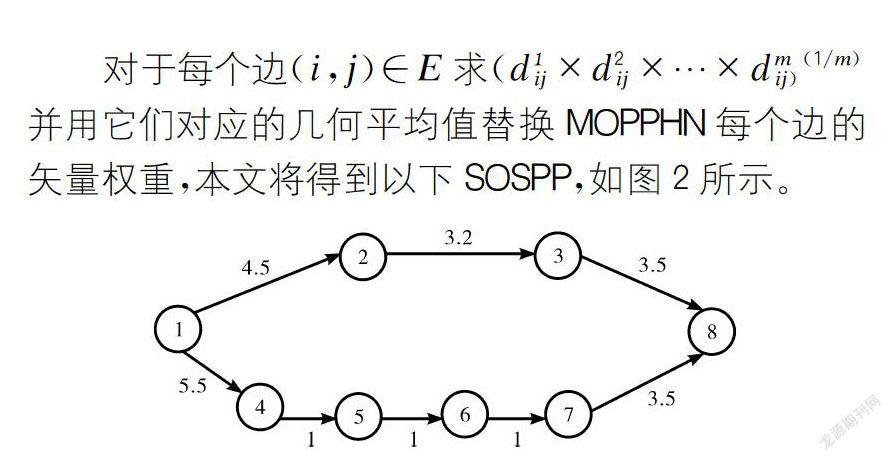
考虑以下网络的MOPPHN来说明上述说法,如图1所示。
第一个最短路径(1,2,3,8)的值是11.2;第二个最短路径(1,4,5,6,7,8>的值是12。但第二个最短路径的矢量权重是路径(16,10)支配第一最短路径(17,10)的矢量权重。因此,使用几何平均值将MOPPHN减少为SOSPP后确定的最短路径不是帕累托最小值。
3 实验与结果分析
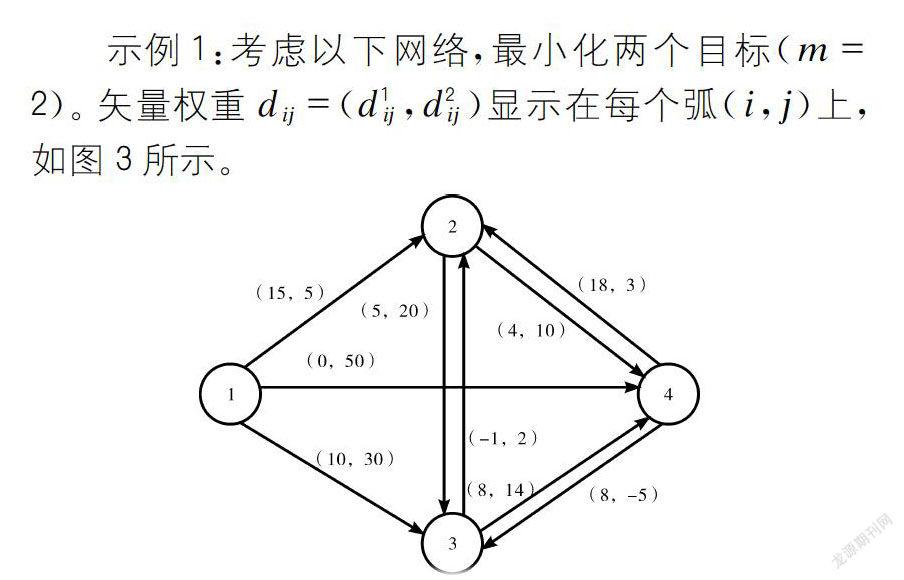
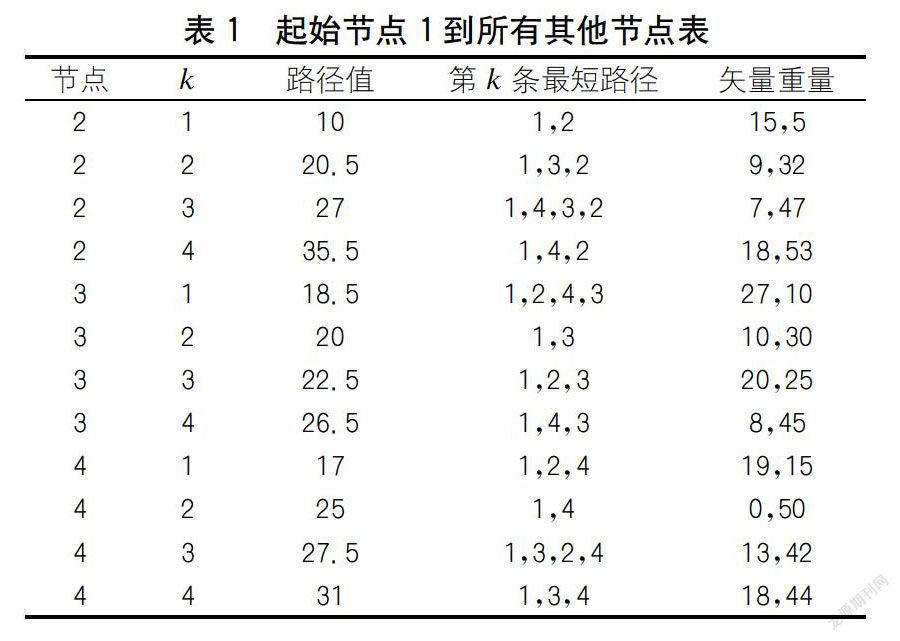
解决方案:应用所提出的算法,从步骤2到步骤3,本文得到以下前四个最短无环路径(k=2)及其矢量权重,从起始节点1到所有其他节点(见表1)。
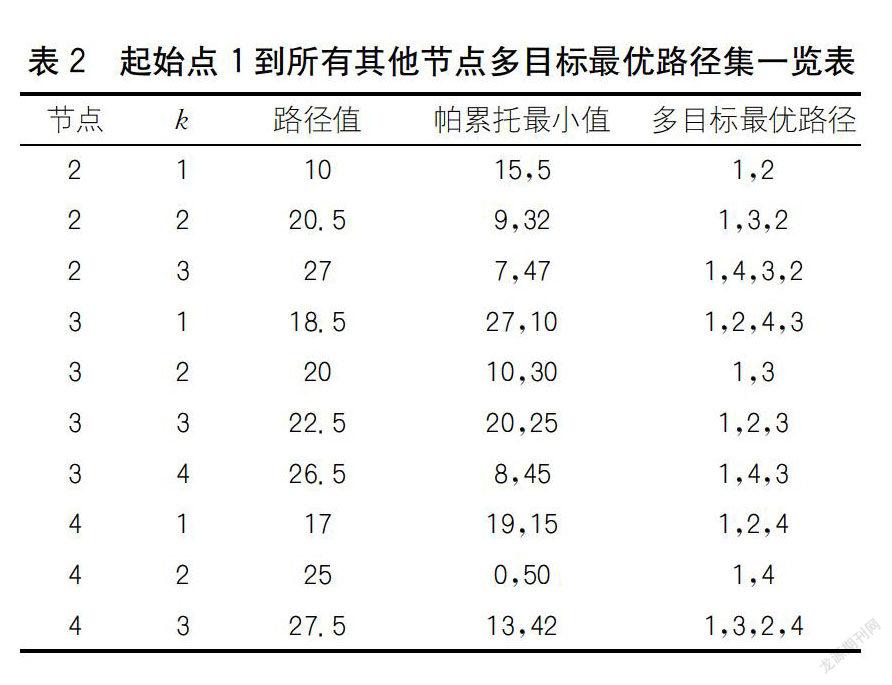
在算法结束时,本文从起始节点1到所有其他节点获得以下多目标最优路径集(见表2)。
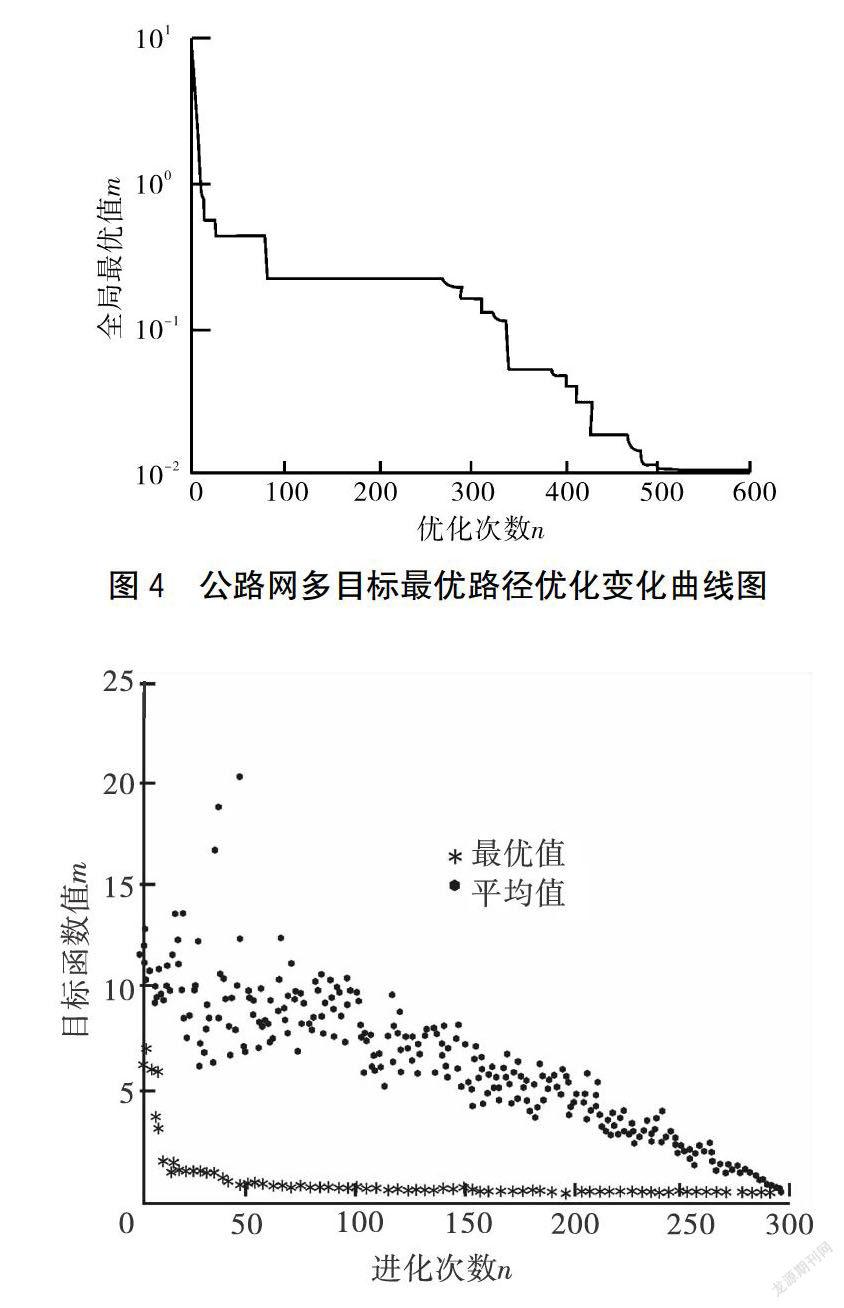
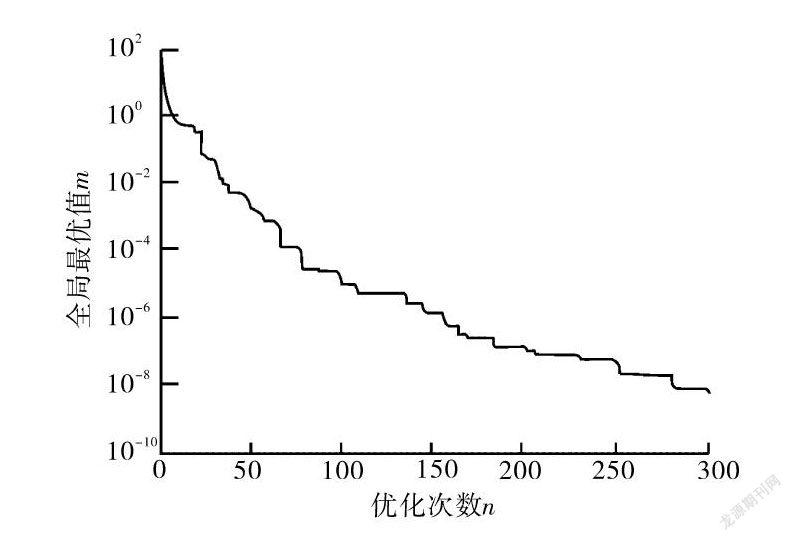
图4为采用普通目标最优路径算法的最优值变化曲线,图5为采用遗传算法得到的目标函数最优路径最优解及最优路径均值变化曲线,图6为采用MOPPHN算法的评价函数最优值的变化曲线。图6中横坐标为最优次数,纵坐标为评价函数的全局最优值。
从图6中可以看出基于公路网多目标最优路径优化进行路径规划的全局最优值在300次最优时已经达到6.79x 10,且单调递减,收敛速度快且精度高。而采用普通公路网多目标最优路径优化和遗传算法仿真得到的结果,从图4中可看出普通目标最优路径算法全局最优值在600次最优时仅为4.178x10,甚至包括一段几手不变的区域,这表明普通公路网多目标最优路径优化仿真速度慢且容易陷入局部最优。遗传算法目标函数最优路径最优解及最优路径均值变化曲线进化300代得到目标函数最优值为0.013987。仿真结果充分显示了MOPPHN算法强大的搜索最优参数的能力。
4 结语
在最坏情况复杂度下,生成从指定源节点到网络MOPPHN中所有其他节点的所有多目标最优路径的现有算法是指数级的。这里提出的算法是在网络层次拓扑结构内多目标最优路径的值的子集。所提出的算法使用算术平均技术将给定的网络MOPPHN减少为SOSPP,已证明相关定理支持该算法。使用所提出的算法,本文可以解决任何具有正或负或两者權重的循环和非循环网络的MOPPHN。本文甚至可以将等级分配给MOPPHN的多目标最优路径的值。如果网络的MOPPHN具有负循环,则所有现有算法仅指示负循环的存在,即指数操作之后也是如此。但是,应用本文提出的算法,本文可以找到网络中任何MOPPHN的一组多目标最优路径,即使它包含负循环。该算法在实际和理论上都表现良好。

