一种用于大范围优化的随机主导学习群优化算法
徐洪斌 李田军 方明亮 李飞
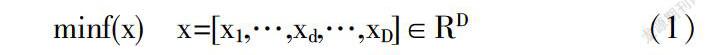
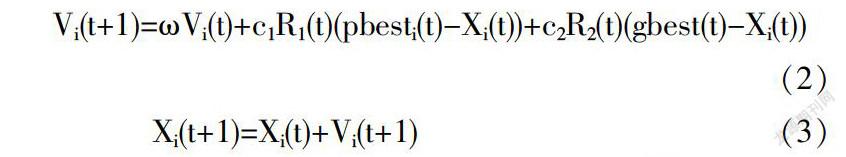


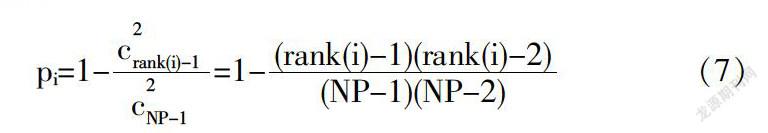

摘 要:针对常规进化算法在求解大范围优化问题时面临计算时间长、占据空间大等难题,本文提出了一种简单而有效的随机主导学习群优化算法-SDLSO.该算法通过引入支配的概念,即从种群中随机选择两个粒子支配该粒子时,采用速度和位置更新公式对粒子进行学习更新,综合权衡算法的勘探和开采能力.为了协助粒子群跳出局部最优,设计了一种参数自适应更新策略.選择CEC2010大范围测试函数对SDLSO算法和CSO算法进行数值仿真实验,结果表明所提出的算法可以有效求解大范围优化问题.
关键词:大范围优化;高维问题;随机主导学习;粒子群优化算法;参数自适应策略
中图分类号:TP274 文献标识码:A 文章编号:1673-260X(2019)11-0047-04
1 引言
尽管已经证明现有的大多数进化算法(EAs)对解决大规模优化问题[1]很有希望,但它们仍然面临着一些局限性.特别是维数的增加给EAs带来了以下主要的挑战.(1)问题的解决方案空间通常随着维度大小的增加呈指数增长.(2)局部最优数量也可能随着维数的增加而增长.一方面,随着维数的增长,一些单峰问题可能成为具有许多局部最优的多模态问题.另一方面,对于一些多模态问题,不仅局部最优的数量可能增加,而且局部最优周围的局部区域可能变得更宽[2-4].受到这两个挑战的影响,传统的进化算法EAs(如粒子群优化(PSO)[5-8]和差分进化(DE)[9,10])的搜索效率和效率都在急剧恶化.这通常是由“维度的灾难”引起的.虽然已经证明了现有的算法在处理大规模优化时具有良好的性能,但在解决复杂的高维问题时,大多数现有的EAs都需要额外的计算时间(除了函数评估时间)和占用大量的空间来定位大规模优化问题的最优值.随着维数的增加,像这样额外的时间和空间也会增加.
为了高效率地进行大规模优化.本文中,我们设计了一个简单而有效的随机主导学习群优化器(SDLSO),它不仅保留了与经典粒子群算法相同的计算时间,而且在解决高维问题时,由于不使用历史上最好的位置,占用的计算空间要小得多.具体来说,在这个优化器中,只有当粒子被它的两个样本(从当前的群中随机选择的)所支配时,它才会被更新.因为每个更新的粒子只能从其支配者那里学习,我们将这种机制描述为随机主导学习(SDL)策略.此外,为了减轻该优化器对新引入的参数的敏感度,利用粒子的进化信息,对SDLSO进一步设计了一种自适应参数调整策略.
2 预备知识
2.1 最优化问题
在不失一般性的情况下,本文考虑的最小化问题的定义如下:
其中,由D个元素组成的x是要优化的变量向量,D是维度大小.在实际的优化问题中,问题的维数(D)多至几百维,甚至高达千维.本文将函数值作为粒子的适应度.
2.2 粒子群优化
粒子群优化(PSO)是Kennedy和Eberhart于1995年[7]引入的一种功能强大且广泛使用的群体智能范例[11],用于解决优化问题.该算法基于一种简单的机制——模仿社会动物的群体行为,如鸟类植绒.由于其实施简单,PSO在过去几十年中受欢迎程度日益增加.PSO包含一群粒子,每个粒子具有在n维搜索空间中的位置和速度,表示要求解的优化问题的候选解.为了定位全局最优值,使用以下等式迭代更新每个粒子的速度和位置:
其中t是迭代(代)数,Vi(t)和Xi(t)分别代表第i个粒子的速度和位置;ω称为惯性权重[12],c1和c2是加速度系数[13],R1(t)和R2(t)是在[0,1]n内随机生成的两个向量;pbesti(t)是迄今为止发现的第i个粒子的最佳解决方案,通常被称为个人最佳解决方案;gbest(t)是迄今为止所有粒子发现的最佳解决方案,被称为全球最佳解决方案.Kennedy[14]提到c1R1(t)(pbesti(t)-Xi(t))和c2R2(t)(gbest(t)-Xi(t))分别作为认知成分和社会成分.
2.3 相关的进化算法
根据将所有的决策变量一同优化与否,可将大多数现有的进化算法分为基于分解的和基于非分解的.
(1)基于分解的进化算法也称为合作协同进化算法(CCEA),其中合作协同进化(CC)[16]框架主要使用分而治之的策略[15],该机制是将原问题分解为若干个低维的子问题.一个标准的CC[16]算法由分解和优化两个阶段组成.在分解阶段,原优化问题被分解为若干个子问题.基于分解的算法的性能在很大程度上依赖于优化问题的分解策略[17].最近,Sun等人提出了一种递归DG方法(RDG)[18].RDG不仅能大大减少适应度评估,而且分组的准确性极高.在优化阶段,可以根据上下文向量使用EA优化每个子问题.上下文向量是完整的候选解决方案,通常是由来自每个子问题的最佳子解决方案组成的.在优化第i个子问题时,使用上下文向量(不包括第i个子组合)与第i个子问题中的个体组合,形成可以评估的完整候选解.最近,Yang等人提出了基于贡献的CC[16]框架[19]来有效地分配计算资源,该框架可以提高算法的整体性能.
(2)基于非分解的EA和传统的EA一样将所有决策变量一起进化,为了提高优化器的性能,引入了许多新的进化方案和策略.文献中存在着许多该方面的工作.在这里我们主要介绍最近由Cheng和Jin提出的CSO算法[4],其性能良好.在该优化器中,从当前群体中随机选择的两个粒子相互竞争,在竞争后,获胜者直接进入下一代,而输家则通过向获胜者和群体的平均位置学习来更新.该机制称为竞争学习策略.因为CSO在进化过程中可以保持高的种群多样性,所以在处理大规模优化时,具有良好的性能.CSO具有这种高的种群多样性得益于它的学习策略,即直接采用在竞争中的优胜者作为指导粒子学习的范例.因此,CSO算法的性能超过了大多数现有的进化算法.
3 随机主导学习优化算法
3.1 随机主导学习策略
在详细阐述SDLSO的机制之前,我们给出了一个粒子的支配者的定义.具体来说,对于第i个粒子xi,只有当xj的适应度不比xi的适应度差时(即 f(xj)≤f(xi)),才能将群中的粒子xj认为是xi的支配者.然后,考虑在SDLSO中存在一个具有NP個粒子的群,随机主导学习策略的关键步骤如下:
步骤(1):对于每个粒子xi(1≤i≤NP),首先从当前群中随机选择两个不同的样本,分别表示为xb1和xb2(1≤b1,b2≤NP).应该注意到b1≠b2≠i.
步骤(2):然后,将两个样本(xb1和xb2)与xi进行比较.只有当xb1和xb2在适应度方面都优于xi时,即f(xb1)≤f(xi)和f(xb2)≤f(xi),xi才通过向它们学习来更新.否则,xi不会更新并直接进入下一代.
步骤(3):当xi更新时,两个样本之间的较好的一个(假设它是xb1)充当第一个样本,而另一个(xb2)作为第二个样本来指导xi学习.具体来说,xi更新如下:
其中xi和νi分别是第i个粒子的位置和速度向量,xb1和xb2是从群中随机选择的两个不同的粒子,它们与第i个粒子不同但更好,并且xb1在适应度方面优于xb2,即b1≠b2≠i且 f(xb1)≤f(xb2)≤f(xi).至于参数r1,r2和r3在[0,1]内均匀生成,β是[0,1]内的一个控制参数,控制第二样本对更新xi的影响.
首先,在步骤(1)中,SDLSO不使用在经典粒子群算法中使用pbest、ibest或gbest来指导[5-7][20][21]粒子的学习,而是直接采用从当前群中随机选取的两个不同粒子作为样本来更新每个粒子.不同于pbest、ibest或gbest(它们可能保持多代不变),在SDLSO中,学习样本通常是一代一代地更新.此外,两个样本都是随机选择的,因此等式(4)中的两个样本对于不同的粒子可能不同.总之,我们可以看到SDLSO在样本选择中可以保持高的群体多样性.
其次,在步骤(2)中,只有当xb1和xb2在适应度方面都优于xi时,xi才能被更新.通过这种策略,可以为较差的粒子直接进入下一代提供机会,这对于保持高的群体多样性具有相当大的帮助.此外,每个更新的粒子只能从其支配者那里学习,因此SDLSQ也可以保持快速收敛到有希望的区域,因为粒子总是从更好的区域中学习.
最后,在步骤(3)中,xb1和xb2之间较好的一个(假设它是xb1)充当第一个样本,而另一个(xb2)作为第二个样本来指导粒子的学习.两个选定样本之间较好的一个可以保留更多开发搜索区域的潜力,并且还拥有更多有用的进化信息来进化群体.因此,这个样本被作为第一个样本来指导一个粒子的学习,以便更新的粒子可以快速接近有希望的区域.虽然另一个样本稍微差一点,但它可能在探索搜索空间方面具有更大的潜力.作为第二个样本,它可以防止粒子太快地更新移动到更好的粒子.这样,当xb1落入局部陷阱时,更新的粒子可能从局部区域逃离.
3.2 SDLSO的自适应参数调整
在方程(4)中,β控制第二个样本的影响,这可以防止粒子更快地接近第一个样本.具体而言,如果两个选定的样本在其适应度方面存在很大差异,那么它们在勘探和开发方面的潜力可能存在很大差异.在这种情况下,β应该很小,以便可以快速找到有希望的区域.但是,如果这两个样本在适应度方面非常相似,那么很可能它们在勘探和开发潜力之间保持很小的差异,因此β应该很大,以增强第二个样本的影响,以便一旦第一个样本落入局部区域,就可以加强预防以避免局部陷阱.
基于上述考虑,我们为β设计了一种自适应调整策略,具体如下:
其中βi是方程(4)中第i个粒子的β值,xb1和xb2是两个选择的样本,它们在适应度方面都优于xi,而且xb1优于xb2,即f(xb1)≤f(xb2)≤f(xi);exp(·)是以e为底数的指数函数,ξ是用于避免零分母的小正值.
从方程(6),我们可以得到三个结果.(1)不同的粒子可能有不同的β值.(2)如果两个选定的样本在适应度方面有很大差异,β很小并且接近0.3.当它们的适应度之间几乎没有差异时,β很大并且接近0.5.(3)特别地,在早期阶段,样本之间的适合度通常存在很大差异,因此β通常很小.但是,随着进化过程的进行,样本之间的适应度的差异变得越来越小.因此,β逐渐变得越来越大.特别是到了后期,由于后期粒子之间的适合度存在微小的差异,所以每个粒子的β值通常都很大.β的这种变化符合粒子在早期快速定位有希望的区域,在后期有效开发有希望的区域,从而不会严重丧失多样性的期望.
从式(4)可以看出,我们可以看到,只有当两个选定的样本都是它的支配者时才更新这个粒子;否则,它将存活并直接进入下一代.具体而言,一个粒子的隐含生存概率可以计算如下:
其中pi是第i个粒子的生存概率,c是从(NP-1)个元素中选择两个元素时的组合数,rank(i)是在以适应度的升序对群组进行排序之后的第i个粒子的排名.从方程(7),我们可以得到三个观察结果.(1):在每一代中,前两个最佳粒子的存活概率均为1.换句话说,这两个粒子总能存活并直接进入下一代.(2):最坏粒子的存活概率为0,表明每一代中最差的粒子总是更新.(3):至于其他粒子,粒子越好,它的存活概率就越高,反之亦然.总之,不同的粒子具有不同的存活机会,这有利于SDLSO维持高的搜索多样性.
总的来说,我们可以看到利用粒子的进化信息,这种调整策略可以在进化过程中自适应地调整每个粒子的β.
3.3 复杂性分析
总而言之,算法1给出了所提出的SDLSO的伪代码.
Algorithm 1: The pseudocode of SDLSO
Input: swarm size NP, maximum fitness evaluations FESmax
1: Initialize particles randomly and calculate their fitness;
2: fes=NP
3: While (fes≤FESmax) do
4: For i =1:NP do
5: Select two random exemplars from the swarm:xb1,xb2;
6: If (f(xb1)≤f(xi) && f(xb2)≤f(xi)) then
7: If (f(xb1)≤f(xi)) then
8: Swap b2 and b1
9: End If
10: Compute βi according to Eq.(6);
11: Update particle x_i according to Eq.
(4) and Eq.(5);
12: Calculate the fitness of xi: f(xi);
13: fes++;
14: End If
15: End For
16: End While
17: Obtain the globa l best solution gbest and its fitness f(gbest);
Output: f(gbest) and gbest
从这个算法中,我们可以看到SDLSO直接利用当前群中的支配者粒来指导粒子的学习.除了函数评估时间,在每一代中SDLSO的计算时间都是O(NP×D)用于更新粒子,这些计算时间是不可避免的.因此,在计算时间上SDLSO和经典的PSO[6-7][22]保持相同的效率.
至于空间复杂性,SDLSO占据了O(2×NP×D)的空间来存储群,其中O(NP×D)的空间保持粒子的位置,另一个O(NP×D)的空间存储粒子的速度,这两者都是不可避免的.由于在SDLSO中没有使用pbest或lbest,因此与传统的PSO[6-7][22]相比,O(NP×D)的空间可以在SDLSO中被节省.简而言之,SDLSO在时间上仍然与经典PSO一样有效,但在空间占用方面更有效.
4 仿真实验及结果分析
本实验的运行环境为内存8G,Intel i7-7500HQ CPU 2.80GHz,Windows 10 64位操作系统,算法采用MATLAB R2019a实现.为了检验算法SDLSO的有效性,我们在CEC’2010测试函数集上进行了广泛的实验.CEC'2010包含了20个1000-D大型函数,它们是通过引入新特征(例如重叠)对函数的扩展.有关这些函数的详细信息,请参阅[23].在实验时除非另有说明,否则适应性评估的最大次数将设置为6000×D(其中D是维度大小).为了公平起见,使用30个独立运行的均值来评估所有算法的性能.
在不失一般性的前提下,我们选择了四个1000-D CEC’2010函数:完全可分离的单峰F1,部分可分离的单峰F9,部分可分离的多峰F11和F15作为测试平台,适应性评估的最大次数设置为6000×D=6×106.在实验中,为了进行公平的比较,两个算法的群大小都被设置为400.下列四幅图给出了SDLSO和CSO在四个1000-D CEC 2010函数上的性能比较.横坐标代表适应度评估次数,纵坐标代表最佳适应度.
从这些图中,我们可以得到以下实验结果:(1)从图(a)和图(b),我们发现在单峰函数F1和F9上,SDLSO和CSO两者的全局最佳适应度的变化趋势相同,并且SDLSO可以比CSO更快收斂的更好解决方案.在优化的后期,SDLSO在F1上几乎找到了最优值.在F9上,即使没有找到最优值,SDLSO的性能也优于CSO.因为SDLSO在勘探和开发之间比CSO具有更好的平衡.
(2)从图(c)和(d)可以看出,当遇到多峰问题F11和F15时,因为粒子的开发不那么广泛,这两种算法都不能找到全局最优的区域.在收敛速度和解决质量方面,SDLSO仍比CSO具有更好的性能,并且SDLSO在优化后期比CSO拥有更强的勘探和开发能力.SDLSO的这种表现归结于高度的种群多样性,所以SDLSO比CSO有更广阔的应用前景.
5 结论
为了可以消耗尽可能少的计算时间和空间来定位最优值,本文在SDLSO中提出了两个策略:一是只有当从当前群体中随机选择的两个样本是其支配者时,才更新这个粒子.这样,每个粒子都有一个直接进入下一代的隐含概率,因此可以保持高的种群多样性.每个更新的粒子只能从其支配者那里学习,因此也可以实现良好的收敛性.二是为了减轻该优化器对新引入参数的敏感性,进一步设计了自适应参数调整策略.使用CEC’10测试函数对SDLSO算法和CSO算法进行仿真实验比较,结果验证了算法SDLSO在解决方案质量和计算成本达到了竞争性甚至更好的性能.后续工作是将本文算法应用于解决其他实际优化问题中.
参考文献:
〔1〕S. Mahdavi, et al., "Metaheuristics in large-scale global continues optimization: A survey," Inf. Sci., vol. 295, pp. 407-428, 2015.
〔2〕X. Peng, and Y. Wu, "Large-scale cooperative co-evolution using niching-based multi-modal optimization and adaptive fast clustering," Swarm Evol. Comput., vol. 35, pp. 65-77,2017.
〔3〕R. Cheng, and Y. Jin, "Asocial learning particle swarm optimization algorithm for scalable optimization," Inf. Sci., vol.291, pp.43-60, 2015.
〔4〕R. Cheng, and Y. Jin, "A Competitive Swarm Optimizer for Large Scale Optimization," IEEE Trans. Cybern., vol. 45, no. 2, pp. 19-204, 2015.
〔5〕J. J. Liang, A. K. Qin, P. N. Suganthan, and S. Baskar, "Comprehensive learning particle swarm optimizer for global optimization of multimodal functions," IEEE Trans. Evol. Comput., vol. 10, no. 3, pp. 281-295,2006.
〔6〕Y. Shi, and R. Eberhart, "A modified particle swarm optimizer," in Proc. IEEE Congr. Evol. Comput., pp. 69-73, 1998.
〔7〕J. Kennedy, and R. Eberhart, "Particle swarm optimization," in Proc. IEEE Int. Conf. Neural Netw, pp. 1942-1948 vol. 4,1995.
〔8〕W. Dong, and M. Zhou, "A Supervised Learning and Control Method to Improve Particle Swarm Optimization Algorithms," IEEE Trans. Syst., Man, Cybern., Syst., vol. 47, no. 7, pp. 1135-1148, 2017.
〔9〕R. Storn, and K. Price, "Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces," J. Global Optim., vol. 11. no. 4. pp. 341-359, 1997.
〔10〕S. Das, and P. N. Suganthan, "Differential evolution: A survey of the state-of-the-art," IEEE Trans. Evol. Comput., vol. 15, no. 1, pp. 4-31, 2011.
〔11〕J. Kennedy, Swarm Intelligence. Seacaucus, NJ, U.S.A: Springer, 2006.
〔12〕Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” in Proc. IEEE Int. Conf. Evol. Comput., Anchorage, AK, U.S.A, 1998, pp. 69–73.
〔13〕R. Eberhart and J. Kennedy, “A new optimizer using particle swarm theory,” in Proc. Int. Symp. MHS, Nagoya, Japan, 1995, pp. 39–43.
〔14〕J. Kennedy, “The particle swarm: Social adaptation of knowledge,” in Proc. IEEE Int. Conf. Evol. Comput., Indianapolis, IN, U.S.A, 1997, pp. 303–308.
〔15〕Y. Mei, M. N. Omidvar, X. Li, and X. Yao, “A competitive divide-and-conquer algorithm for unconstrained large-scale black-box optimization,” ACM Trans. Math. Softw., vol. 42, no. 2, p. 13, 2016.
〔16〕M. A. Potter and K. A. De Jong, “A cooperative coevolutionary approach to function optimization,” in Parallel Problem Solving From Nature PPSN III. Heidelberg, Germany: Springer, 1994, pp. 249–257.
〔17〕S. Mahdavi, M. E. Shiri, and S. Rahnamayan, ''Metaheuristics in large-scale global continues optimization: A survey,'' Inf. Sci., vol. 295, pp. 407–428, Feb. 2015.
〔18〕Y. Sun, M. Kirley, and S. K. Halgamuge, “A Recursive Decomposition Method for Large Scale Continuous Optimization,” IEEE Trans. Evol. Comput., vol. 22, no. 5,pp.647-661, 2018.
〔19〕M. Yang et al., ''Efficient resource allocation in cooperative co-evolution for large-scale global optimization,'' IEEE Trans. Evol. Comput., vol. 21, no. 4, pp. 493–505, Aug. 2017.
〔20〕J. Kennedy, "Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance," in Proc. IEEE Congr. Evol. Comput., pp. 1931-1938, 1999.
〔21〕J. Li. J. Zhang, C. Jiang, and M. Zhou, “Composite Particle Swarm Optimizer With Historical Memory for Function Optimization,” IEEE Trans. Cybern., vol. 45, no. 10, pp. 2350-2363, 2015.
〔22〕A. LaTorre, S. Muelas, and J.-M. Pena, "A comprehensive comparison of large scale global optimizers," Inf.Sci., vol. 316, pp. 517-549, 2015.
〔23〕K. Tang, X. Li, P. N. Suganthan, Z. Yang, and T. Weise, "Benchmark functions for the CEC 2010 special session and competition on large-scale global optimization," Technical Report, Nature Inspired Computation and Applicattons Laboratory, U.S.TC, China, 2010.

