“留白”，让思维在等待中发散

马也骋

【摘要】绘画留白，留给欣赏者无限的遐想;音乐留白，留给倾听者绵绵的情意;书法留白，留给知音者空灵的空间。作为独特的艺术活动，课堂教学同样需要空白之美，讲究留白艺术。以“空白”为载体，在新旧知识的衔接处“留白”，在学习时空的分配上“留白”，在提出问题的技巧上“留白”，在实践操作的探索中“留白”，在后续学习的延伸处“留白”，进而达到“方寸之地尽显天地之宽”的教学效果。

【关键词】主动思考 释放思想 驱动思维 展开思辨 开启悬念

笔者在闲暇的时间里拜读了《吴正宪给小学数学教师的建议》一书，并对教育教学有了一些新的认识，在读到“把‘空白’留给学生”时，笔者得到一些新的启发。

我们对未知的事物往往会产生一种神秘感，并且总会想法设法了解并知道它，正因为未知产生的“空白”，才充分地调动了观赏者的鉴赏兴趣，艺术上的“空白”既是“无”，又是一种特殊的“有”，是“无”与“有”的辩证统一。课堂教学中也需要“空白”，不能让教师的思维去代替学生的思维，从而产生一言堂的教学诟病，而需要留给学生一些思考和想象的空间，也就是“留白”，让他们自己发现问题、提出问题、分析问题、解决问题。因此本文就以《平行四边形的面积》一课为例，谈谈如何在课堂教学中适度地“留白”，让学生在“此时无声胜有声”的等待中经历悟的顿生、思的深远，以期发散学生不竭的思维，发掘学生持久的学力。

一、在新旧知识的衔接处“留白”，催生主动思考

吴正宪老师在书中讲到“教学《平行四边形的面积》这一课时，我先出示一个长方形的框架，然后轻轻拉动，变成一个‘平行四边形’，继续拉动，学生齐声说‘变矮了’‘更矮了’。这时，我停止拉动，问道：‘长方形变成了平行四边形，你们猜面积变没变？’”一开始读到这里，笔者将信将疑，想到这个问题是书上的一道练习题，很多学生在做题目时都理解不了，甚至到了期末复习的时候，学生还是不理解，如果现在把这个问题抛给学生，是否有点心急。后来，笔者转念一想，吴老师巧妙地将新旧知识联系在了一起，在学习平行四边形的面积前，学生已经掌握了长方形的面积知识，知道长方形的面积公式是“长×宽”，通过演示将长方形拉成平行四边形这一过程，抛出问题：“平行四边形的面积变了吗？”发人深思，让学生有了很强的探索欲望，自然衍生出这些疑惑：

（1）平行四边形的面积有没有变化？

（2）长方形的面积公式我们知道，那么平行四边形是否也有面积公式呢？

（3）能够通过怎样的方法来得出平行四边形的面积公式呢？

……

在新旧知识的衔接处留给学生一个空白，让学生有思考的時间和空间，强大的认知需求激活着学生的探究意识，这种探究意识犹如课堂上的“催化剂”，促使学生主动思考。

二、在学习时空的分配上“留白”，释放学习思想

在数学教学中，讲台似乎是教师神圣不可侵犯的领地，站在讲台上的教师滔滔不绝地讲着新授的内容，一节课40分钟虽然说很辛苦，但是有时教学效果并不理想。其实教师有时可以留一些“空白”给学生，让学生上台来演示，说说自己是怎么想的。

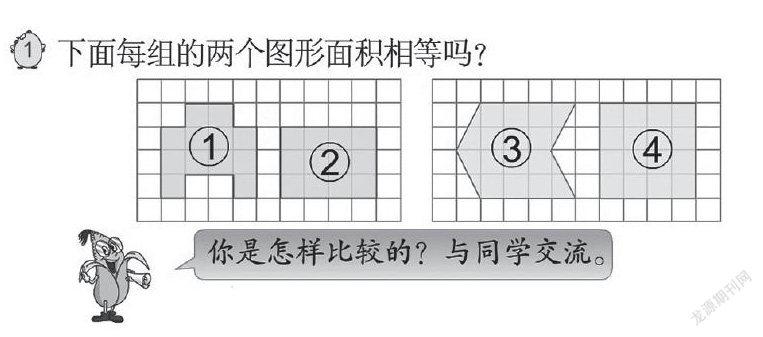
在苏教版五年级上册《平行四边形的面积》中，第一个例题便是比较上面两图的面积是否相等，教师可以将讲台的位置留给学生，让学生用自己的话来解释：每组的两个图形面积是否相等？是怎样比较的？在解决问题的方法上有什么不同？在锻炼学生的语言表达能力的同时，还可以指引学生用“我有不同的想法……”“我对某某同学的发言进行补充”“我认为运用转化的方法更有优势，因为……”进行发言。这样，就有助于学生更加专注地倾听同伴发言，取长补短，这样教师就可以自然而然地将学生引入运用基本数学思想解决问题的轨道上来。

三、在提出问题的技巧上“留白”，驱动多向思维

教师精心设计恰到好处的停顿，给学生造成知识上的“空白”，当学生发现从教师所讲和现成教材上得不到自己所缺失的知识时，那段设置的“空白”便会吸引他们，于是学生会急不可待地调动思维去积极探索这个问题。

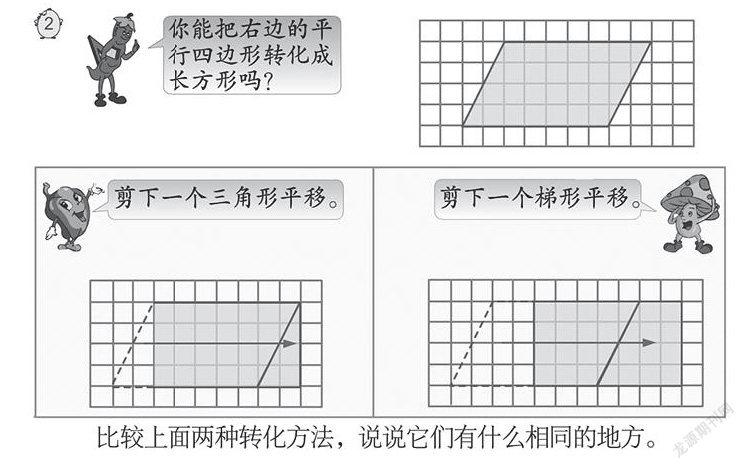
《平行四边形的面积》这节课第二个例题中最后有一个问题：上面两种转化的方法，有什么相同的地方？这个问题可以抛给学生独自思考解决，几次尝试，学生会发现：“只要沿着平行四边形的高剪下一个图形，通过移、拼就可以转化成一个长方形。转化后，图形的周长变了，面积不变。”这时候学生可能隐隐会有一种感觉——平行四边形的面积会不会与其高有关系呢？虽然这只是学生凭着感觉的一种猜想，但笔者想，只要有了这样的猜想，学生就会付诸行动，驱动多向思维来想方设法解决问题。

留一些时间“空白”给学生，学生就会有验证的意识、思索的空间、思维的多向，能够自主地发现和解决问题，这不仅能够使学生牢记知识点，而且还能培养学生的兴趣。

四、在实践操作的探索中“留白”，展开过程思辨

通过实践操作以及小组合作记录、讨论、思辨，学生能够更加清晰地知道长方形的长和宽与平行四边形的底和高之间的对应关系，从而能够比较轻松地从长方形面积的计算公式推导出平行四边形的面积计算公式。

学生自主发现平行四边形的面积公式，不只是能够让他们深深地记住这一公式，更重要的是学会如何将平行四边形转化成长方形从而推导出面积计算公式的方法，渗透了从未知转化到已知的数学思想，为接下去推导出三角形的面积公式、梯形的面积公式作铺垫。

五、在后续学习的延伸处“留白”，开启悬念思索

众所周知，平行四边形的面积公式是通过“剪、移、拼”将平行四边形转化成长方形的面积推导出来的。其实，三角形的面积公式以及梯形的面积公式也是通过转化的方法，那么我们可以在下课前3分钟给学生留一个“空白”——“平行四边形是通过转化的方法将其转化成长方形的面积推导出来的，那么三角形、梯形的面积公式是否也可以通过转化推导出来呢？有兴趣的同学课后可以去试试，再和老师进行交流。”简单的一个“留白”，又激起了学生浓厚学习兴趣。

留白不是俭省，也不是避重就轻，而是引而不发，是一种教学智慧。注重课堂教学的留白之妙，把握课堂教学的留白之时，感受课堂教学的留白之美，课堂的留白就是学生的充实，教师的不讲就是学生的思考，教育的美好就在于此！

【参考文献】

吴正宪，王彦伟，韩玉娟. 吴正宪给小学数学教师的建议[M].上海：华东师范大学出版社，2012.