基于双采样点的双向RRT路径规划算法
闫明亮 侯光华
摘要:传统快速扩展随机树(RRT)算法在生成采样点时采用随机扩展的策略,导致路径的生长无方向性且路径规划速度较慢。针对此问题,在采样点选取策略上采用双采样点的方法,同时随机生成2个采样点,并选取其中距离目标点较近的点作为最终采样点,可使路径的生长在一定程度上具有方向性,提高路径规划的效率。仿真试验中,与传统RRT和双向RRT路径规划算法进行对比分析,验证了算法的有效性。
关键词:快速擴展随机树;双向RRT路径规划;双采样点
中图分类号:TP301.6文献标志码:A文章编号:1008-1739(2019)15-55-4

0引言
路径规划是指在某种环境内,按照一定的评价标准,如路径最短或规划时间最少等,寻找一条从起始点到目标点的无碰撞路径[1]。
目前,一种传统的路径规划算法是基于采样的快速扩展随机树[2]算法。但由于在RRT的扩展过程中,采样点的选取使用全局的均匀随机采样策略[3],导致路径搜索效率低[4]。由此提出了双向RRT(Bi-RRT)算法,从起始点和目标点同时生成2棵RRT并进行相向扩展,加速了算法的收敛速度[5]。但节点的扩展方式仍使用在全局环境中进行均匀随机采样的策略,缺乏目标导向性,降低了路径规划效率[6]。
为解决上述方法出现的问题,提出一种基于双采样点的双向RRT路径规划(DBi-RRT)算法,该算法在随机点采样策略上使用双采样点方法对随机点进行采样,减少过多无用节点扩展的同时使得随机树的生长具有方向性。
1双采样点的双向RRT算法
1.1算法原理
本算法分别以起始点和目标点为根节点,同时生成2棵随机树进行相向生长,通过2次随机采样生成2个随机采样点,比较2个候选采样点与目标点的距离大小,选取距离较小的点作为最终采样点,使得随机树具有一定的方向性。
双采样点示意图如图1所示,同时随机生成2个候选采样点rand1,rand2,比较2个点到目标点goal的距离,可知|rand1, goal|<|rand2,goal|,因此选取rand1作为最终采样点rand,进而对随机树进行扩展得到扩展节点new。若对随机树进行扩展,则将起始点init作为目标点,采用相同的方法进行判断和扩展。本方法可解决传统随机采样随机性太大,不具有方向性,路径规划效率低的问题。

2实验与分析
为验证DBi-RRT算法的性能,选取了2种不同的环境地图进行仿真试验,在每种环境地图中将本文算法分别与传统RRT和DBi-RRT算法进行对比分析。
如图3所示,为充分模拟现实环境中的障碍物,本文设置了2种不同环境的试验地图。试验地图1中为形状不规则的障碍物,且障碍物有大有小;试验地图2中为外形规则的障碍物。2种地图中障碍物分布都不均匀。地图尺寸大小均为 800×800,起始点和目标点坐标均为[20,20],[780,780]。仿真实验均在CPU为Intel Core i5-3210M, 2.5 GHz,内存4 G的计算机上进行,编程环境为Matlab R2013b。

2.1地图1试验
将DBi-RRT算法分别与RRT和Bi-RRT算法在试验地图1中进行路径规划对比分析,在地图1中将3种算法分别运行30次,取其中的一次运行结果如图4所示,记录每次路径规划所用时间、算法迭代次数和所规划路径的长度。

由试验地图1中的运行结果可知,RRT算法由于在采样策略上使用全局范围内的均匀随机采样方法,生成了大量的无用节点;Bi-RRT算法相对RRT算法,大大减少了无用节点的生成;DBi-RRT算法只有少量的无用节点,使得算法的迭代次数显著减少,加速了路径规划的速度。3种参数的对比分别如图5、图6和图7所示,将3个参数的记录值分别求取平均值进行对比分析如表1所示。
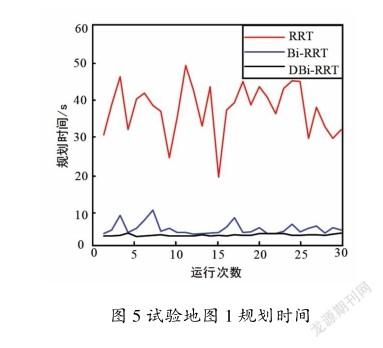
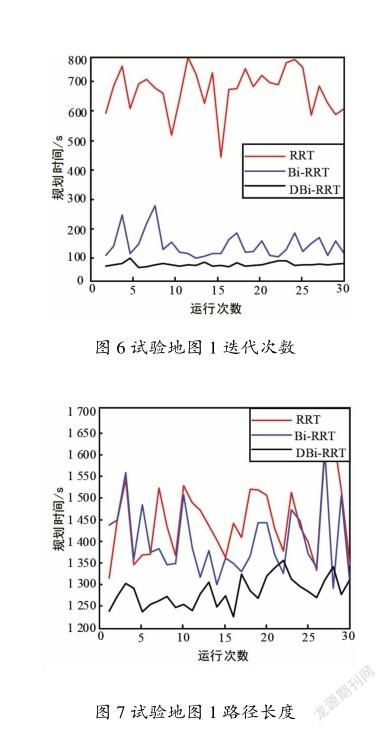
由3幅图可知,DBi-RRT算法在路径规划时间、算法迭代次数和规划路径长度上均优于RRT, Bi-RRT算法。
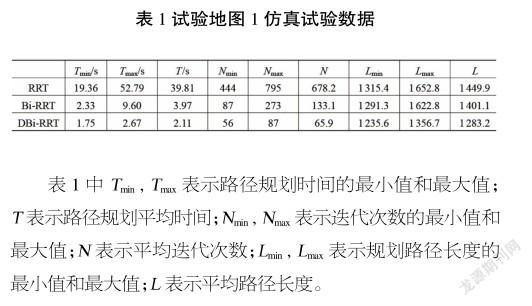
由表中数据可得,在平均规划时间方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别缩短了94.70%, 46.85%;在平均迭代次数方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别减少了90.28%, 50.48%;在平均规划路径长度方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别减少了11.50%, 8.4%。
2.2地图2试验
将DBi-RRT算法分别与RRT和Bi-RRT算法在试验地图2中进行路径规划对比分析,在地图2中将3种算法分别运行30次,取其中的一次运行结果如图8所示,记录每次路径规划所用时间、算法迭代次数和所规划路径的长度。
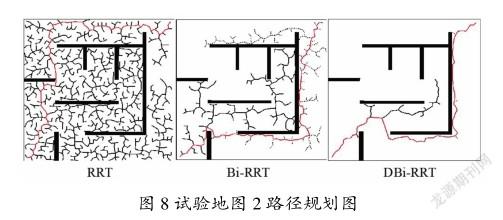
由试验地图2中的运行结果可知,RRT算法生成了大量的无用节点,布满整个地图;Bi-RRT算法相对RRT算法,无用节点数量大大减少;DBi-RRT算法的无用节点数量最少,3种参数的对比如图9、图10和图11所示,将3个参数的记录值分别求取平均值进行对比分析如表2所示。

由图可知,DBi-RRT算法在路径规划时间和算法迭代次数相对于RRT和Bi-RRT算法均有较大优势。
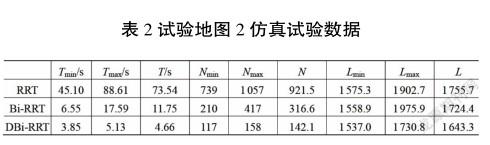
由表中数据可得,在平均规划时间方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别缩短了93.66%, 60.34%;在平均迭代次数方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别减少了84.57%, 55.11%;在规划平均路径长度方面,DBi-RRT算法相对于RRT, Bi-RRT算法分别减少了6.4%, 4.7%。
通过以上仿真试验及数据分析,本文提出的DBi-RRT路径规划算法,由于采用了双采样点方法,使得在路径规划过程中路径的生长具有了方向性,大大减少了无用节点的扩展,减少了算法的迭代次数,显著提高了路径规划的效率。
3结束语
DBi-RRT算法在采样点的选取方式上进行了改进,双采样点方法的使用使得随机树的扩展具有了方向性,大大提高了路径的规划速度。仿真试验结果表明:DBi -RRT算法相对于 RRT, Bi-RRT算法在路径规划时间和算法迭代次数上均有较大提升,极大提升了路径规划的效率。提出的算法可应用于室内服务机器人的路徑规划应用领域,在指定目的地后,服务机器人可根据环境地图快速规划出行走路径,提高服务质量。
参考文献
[1]宋金泽,戴斌,单恩忠.一种改进的RRT路径规划算法[J].电子学报,2010,38(1): 225-228.
[2]莫栋成,刘国栋.改进的RRT-Connect双足机器人路径规划算法[J].计算机应用,2013,33(8):2289-2292.
[3]杜明博,梅涛,陈佳佳,等.复杂环境下基于RRT的智能车辆运动规划算法[J].机器人,2015,37(4): 443-450.
[4]王道威,朱明富,刘慧.动态步长的RRT路径规划算法[J].计算机技术与发展,2016,26(3):105-107.
[5]孙丰财,张亚楠,史旭华.改进的快速扩展随机树路径规划算法[J].传感器与微系统,2017,36(9):129-131.
[6]陈波芝,陆亮,雷新宇.基于改进快速扩展随机树算法的双机械臂协同避障规划方法[J].中国机械工程,2018,29(10): 1220-1226.

