主成分分析和支持向量机在无刷直流电机故障诊断中的应用研究

钟书辉 段丽华 王炜 邓友成

摘要：针对无刷直流电机（BLDCM）故障诊断问题，提出一种基于主成分分析（PCA）和支持向量机（SVM）的故障诊断方法。首先对故障时刻无刷直流电机三相电流进行分析，提取故障特征值;再由PCA从提取的故障特征值中选取敏感特征;最后使用SVM对特征值集合进行训练和测试，实现故障诊断与识别。该方法在6种无刷直流电机典型故障中进行了验证，故障诊断准确率高达92%，证实了该方法的有效性。

关键词：无刷直流电机;故障诊断;特征提取;主成分分析;支持向量机

中图分类号：TM33 文献标识码：A

无刷直流电机（Brushless DC Motor，BLDCM）因其结构简单、寿命长、效率高等特点，已在航空、航天、航海、兵器等诸多领域得到广泛应用。对BLDCM运行状态进行监测，提高BLDCM的可靠性和安全性也成为研究热点M。目前，BLDCM的故障诊断主要分为基于模型和基于信号处理技术两大类。基于模型的BLDCM故障诊断方法多通过构建高精度数学模型来实现对BLDCM甚至整个系统的故障诊断[3～5]。然而由于BLDCM的非线性特性，使得构建精确模型较为困难。

近年来，随着数字信号处理技术的快速发展，采用合适信号作为故障诊断的信号源，研究其特征与故障的对应关系已成为BLDCM故障诊断新的研究趋势。对于大中型BLDCM，多采用加装加速度传感器等方法来获取电机运行时的振动信号，通过对振动信号的分析，提取故障特征值，确定故障类型[6]。但此方法不适用于微型BLDCM。因此，又有学者提出将电机的母线电流作为故障诊断的信号源，可检测电机及电机驱动器、齿轮组、轴承、永磁体等故障[7～13]。该方法不需要增加额外传感器，且随着计算机及其相关技术的迅猛发展，已得到了越来越广泛的应用。

如果以BLDCM发生故障时三相电流作为故障信号源，由于故障发生时信号多为瞬态、冲击、非平稳信号。从BLDCM三相电流中提取故障特征值，获取数值较多，造成故障诊断的计算复杂度較高。为此，需要找到可以减少故障特征值数量，同时又能反映故障特征的方法，以降低故障诊断的复杂性。

主成分分析（Principal Components Analysis，PCA）法是一种多元统计方法，它能够对原始的特征矩阵进行降维处理，降低数据的复杂程度，并且还能够保留原始特征空间中的主要信息。在故障诊断中应用广泛[14，15]。支持向量机（Support Vector Machine，SVM）法因所需样本数量较少，支持非线性系统等优点在故障诊断中应用也较为普遍。

本文提出基于PCA和SVM的BLDCM故障诊断方法。首先对BLDCM三相电流在各种典型故障下的信号进行分析，提取故障特征值。再利用PCA对提取的故障特征值进行分析，找出敏感特征，在保障故障可被识别的前提下减少故障特征值数量。最后利用SVM进行训练和测试，实现故障诊断。通过BLDCM驱动器、霍尔信号等实际故障诊断，证明该方法的有效性。

1 故障特征提取

1.1 BLDCM组成及典型故障

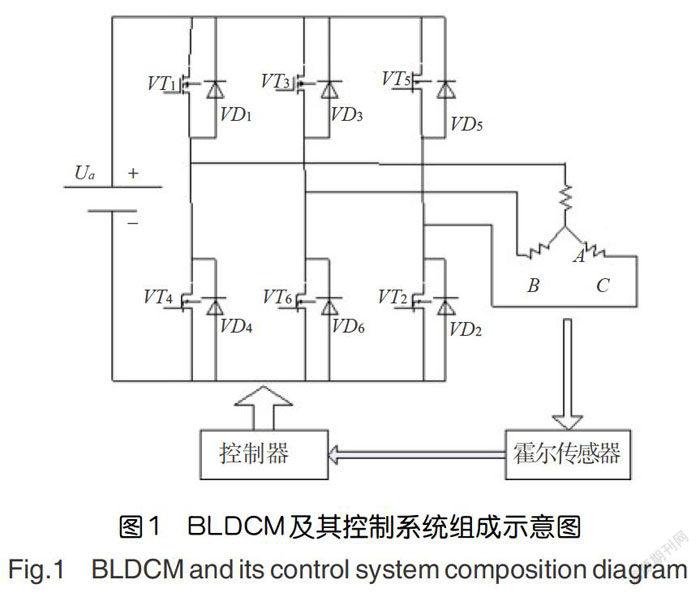
图1为BLDCM组成示意图，可知BLDCM主要由电源、驱动电路、控制器、电机本体和霍尔传感器等5部分组成。其中电源和驱动电路负责根据控制器的指令对驱动电路中的MOSFET开断进行控制，从而达到改变BLDCM工作电压，进而实现BLDCM控制。霍尔传感器对BLDCM的转子位置进行检测，将结果传递给控制器，由其根据相关算法控制驱动电路[16]。

根据BLDCM组成可知，其主要故障发生在各组成部分，其中逆变电路故障和霍尔传感器故障因其具有故障比例高、危害大等原因[17，18]，可作为BLDCM的典型故障。

1.2 故障特征

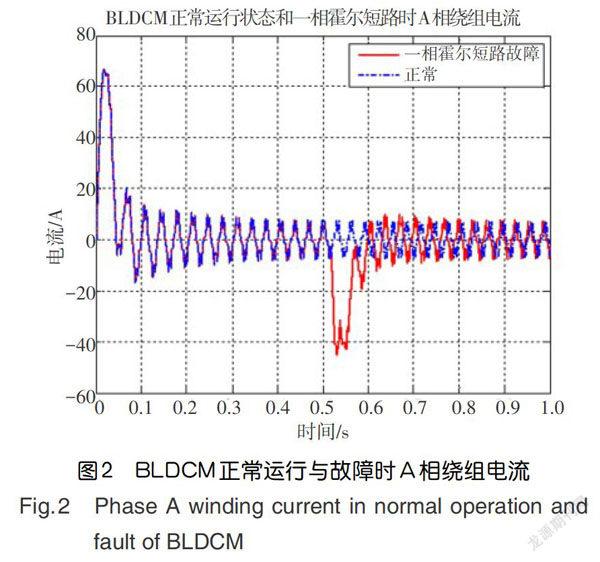
图2为BLDCM正常状态和一相霍尔信号短路故障时A相电流波形。由此可知BLDCM的三相绕组电流信号表现为周期性信号，故障发生时电流信号会产生变化，不同故障类型的电流信号特征也不同。因此可将三相电流故障时电流波形作为故障信号源[19，20]。通过分析故障时三相电流波形的波形指标（如峰值指标、脉冲指标、裕度指标、峭度指标等）和波形的统计量（如极差、电流变化率、均值、均方值、峰值等）作为故障特征值。

2 PCA数据降维

主成分分析法可将多个变量通过降维技术，转化为少数几个主成分即可表示原始变量大部分信息的技术。PCA的运用可使数据维度减少，降低了数据处理复杂程度，避免了维度灾难[21]。

在PCA应用于故障诊断时，一般遵循以下步骤：

（1）确定每个样本包含的故障特征值数量为P，总共包含k个样本，则由全部样本组成原始故障特征矩阵X（k×p），对X进行归一化处理，得到新的故障特征值矩阵X1。

（2）计算X1的协方差矩阵S。

（3）计算S的特征值和特征矢量。

（4）计算主成分得分矩阵Y。实现原始矩阵X在主成分空间的转换。

（5）计算Y中所有主成分的累计贡献率。当Y中前m个主成分的累计贡献率达到人为设定的阀值E时（一般累计贡献率达到90%及以上），则原始矩阵X的主成分个数为m。

由此可知，PCA可使位于高维的故障特征样本通过转换，投影到一个新的低维特征空间中，实现降维的目的。

3 基于SVM的故障诊断

支持向量机具有通用性好、鲁棒性强、计算简单等优点，同时SVM不涉及所需解决问题的内部问题，因此应用广泛[22]。SVM采用核函数将故障特征矢量映射到高维特征空间中，并在该高维空间中构造一个分类超平面作为决策曲面，将样本划分开。在该过程中，SVM中的核函数对于SVM的性能产生很大的影响。常见的SVM核函数P主要有：

（1）线性核函数

P（q，q）=q，q

（2）多项式核函数

P（q，q）=（γqq+u），γ>0

（3）径向基核函数

P（q，q）=exp（-γ‖q·q‖），γ>0

（4）两层感知器核函数

P（q，qj）=tanh（γqq+u）式中：q为输入矢量;q为第i个输入矢量;γ，u为常数。

上述4种基函数中以径向基核函数最为常用。合适的核函数将会使SVM学习速度较快、泛化性较强。

日常故障诊断中，需要对多种故障进行有效识别和分类，为此，SVM需要构造合适的多类分类器。目前，常见的SVM多类分类器可分为直接法和间接法两种。直接法是将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类[23]。但该方法计算复杂度比较高，实现起来比较困难。间接法是通过组合多个二分类器来实现多分类器的构造，又分为一对多法和一对一法两种。

（1）一对多法

训练时依次把某个类别的样本归为一类，其他剩余的样本归为另一类，分类时将未知样本分类为具有最大分类函数值的那类。

（2）一对一法

其做法是在任意两类样本之间设计一个SVM，当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。一对一法因为不会出现不可分的现象，具有较高的分类准确率。因此本文采用一对一法的SVM。

4 实例分析

4.1 故陈特征提取

根据BLDCM工作原理，在Matlab/Simulink中搭建BLDCM仿真模型，如图3所示。

选取单个霍尔信号故障（短路、断路）、单个MOSTET故障（短路、斷路）、两个MOSTET故障（不在同一桥臂上的两个MOSTET），正常工作状态4种故障模式。其中霍尔信号故障共计有3×2=6组故障模式。单个MOSTET则为6×2=12组故障模式，两个MOSTET则有12×4=48组故障模式，总计67种故障模式。每种故障模式样本个数为56个，所以故障模式样本总共67×56=3752组。

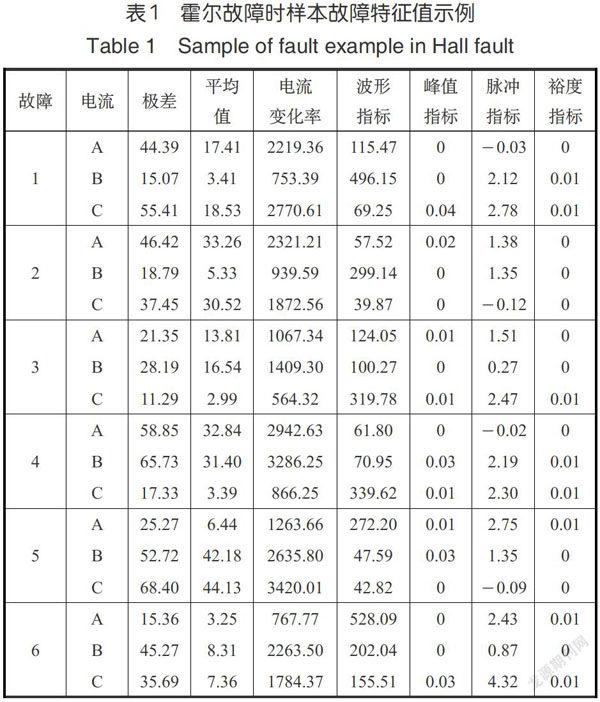
对于每一个故障模式样本中的三相电流，分别提取故障时电流波形的极差、平均值、电流变化率、波形指标、峰值指标、脉冲指标、裕度指标等7个特征值作为故障特征值。由于篇幅限制，仅将霍尔故障时三相电流各一个样本（1，霍尔A短路;2，霍尔A断路;3，霍尔B短路;4，霍尔B断路;5，霍尔C短路;6，霍尔C断路）的故障特征值给出，见表1。其余故障样本由于篇幅所限，不再一一列出。

4.2 PCA分析

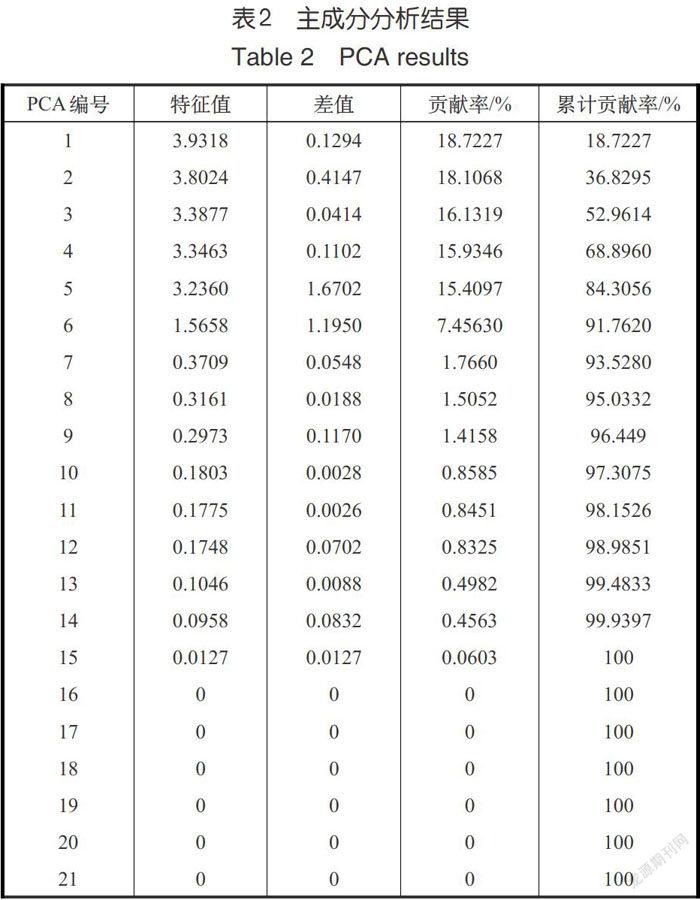
对所有故障样本组成的故障特征组（3752×21）进行PCA主成分分析，依次计算21个主成分的累计贡献率，结果见表2。前7个主成分（每个故障样本中A相电流故障特征值）的累计贡献率已经达到93.528%。因此原来故障特征组（3752×21）经主成分分析后，可转化为新的故障特征组（3752×7）。

4.3 SVM故障识别及结果

将每个故障的56组故障样本分为测试集和验证集，分别包含40组故障样本和16组故障样本。并对每种故障类型设置不同的标签。故SVM的测试集总共有67×40=2680组故障样本，测试集则有1072组故障样本。

为验证PCA分析结果，故障特征值采用了两种方式，分别为A相电流故障特征值和三相电流故障特征值，即每个故障样本包含的故障特征值数量分别为7个和21个。

SVM采用径向基函数作为核函数，分别对PCA降维和原始故障数据分别进行SVM训练和测试，在惩罚参数和核函数参数分别取900和80时，经过PCA降维的故障特征数据识别率为86.47%（927/1072），SVM训练和测试时间为4.359s。在惩罚参数和核函数参数分别取808.6和37.7时，原始故障特征数据识别率为92.26%（989/1072），SVM训练和测试时间为9.137s。可见，经过PCA降维后的故障特征数据集在SVM中的识别率较原始故障特征数据集训练的识别率相差5.79%，但时间上节约一半左右。

利用PCA降维故障数据，分别采用BP神经网络，径向基函数神经网络和自组织特征映射神经网络进行训练和测试，得到的故障识别率分别为63.4%、71.5%和73.6%。较以上由SVM神经网络得到的92%故障识别率有着较大差距，说明选取SVM神经网络的正确性和有效性。

5 结论

利用BLDCM故障发生时三相电流波形，提取故障特征值，通过PCA运算得到降维的故障特征数据集。将降维后的故障特征数据集和原始故障特征数据集分别在SVM中进行训练和测试，结果表明PCA降维可显著减少数据计算复杂程度，同时不会对数据识别率产生较大影响。SVM对多类故障识别具有很好的识别效果。

参考文献

[1]夏长亮.无刷直流电机控制系统[M].北京：科学出版社，2009.Xia Changliang.Brushless DC motor control system[M].Beijing：Science Press，2009.（in Chinese）

[2]张媛，陈宏韬，赵嵩.航天用无刷直流电动机故障模式及危害性分析[J].微特电机，2015，43（2）：27-30.

[3]杨秉岩，程绍成，朱伟，等.基于传递函数识别的导弹电动舵机故障诊断[J].海军航空工程学院学报，2012，27（5）：494-498.

[4]史贤俊，张文广，张艳，等.PSO-RBF神经网络在舵机系统故障诊断中的应用田.海军航空工程学院学报，2011，26（2）：131-135.

[5]廖瑛，吴彬，曹登刚，等.基于自适应观测器的导弹电动舵机故障诊断研究[J].系统仿真学报，2011，23（3）：618-621.

[6]刘冬生，赵辉，王红君，等.基于小波分析和神经网络的电机故障诊断方法研究[J].天津理工大学学报，2009，25（1）：11-14.

[7]肖蕙蕙，熊隽迪，李川，等.基于定子电流检测方法的电机故障诊断[J].电机与控制应用，2008，35（1）：54-57.

[8]杨明，柴娜，李广，等.基于电机驱动系统的齿轮故障诊断方法对比研究[J].电工技术学报，2016，31（19）：132-140.

[9]周杨，马瑞卿，李添幸，等.无刷直流电机逆变器双管开路故障仿真研究[J].微电机，2016，49（12）：70-75.

[10]杨欣荣，蒋林，王婧林，等.基于小波变换的无刷直流电机逆变器故障诊断[J].电测与仪表，2017，54（5）：113-118.

[11]程啟华，盛国良.無刷直流电动机匝间短路故障检测及识别方法[J].微特电机，2014，42（2）：14-17.

[12]刘昕彤，王红艳，张冬梅，等.无刷直流电机在转子偏心故障时的容错控制研究[J].电机与控制应用，2017，44（5）：121-127.

[13]潘汉明，雷良育，王子辉.基于小波分析的电动汽车轮毂电机永磁体故障诊断[J].中国机械工程2016，27（11）：1488-1492.

[14]张宇飞，么子云，唐孙林，等.一种基于主成分分析和支持向量机的发动机故障诊断方法阴.中国机械工程，2016，27（24）：3307-3311.

[15]夏梦莹浏啸奔，陈严飞，等.基于主成分分析和自组织神经网络的柴油机故障诊断方法[J].计算机应用，2014，34（z2）：184-185.

[16]柴永利，王炜，何卫国.一种无刷直流电动机故障诊断方法研究[J].微特电机，2018，46（6）：49-52.

[17]杨忠林.基于小波包分解的逆变器一相开路故障诊断[J].电机与控制应用，2011，38（7）：34-37.

[18]刘锴，王宜怀，徐达.无刷直流电机霍尔位置传感器故障处理研究[J].电力电子技术，2017，51（7）：93-96.

[19]黄佳平.基于BP神经网络的直流电弧故障检测技术研究[D].杭州：杭州电子科技大学，2017.

[20]岳巧珍.基于峭度：小波分析的齿轮典型故障诊断方法研究[D].哈尔滨：哈尔滨理工大学，2016.

[21]谢中华.MATLAB统计分析与应用：40个案例分析[M].2版.北京：北京航空航天大学出版社，2016.

[22]王小川，史峰，郁磊，等.MATLAB神经网络43个案例分析IM].北京：北京航空航天大学出版社，2016.

[23]陈维，刘军尧，齐东科，等.基于二叉树支持向量机的某型装备故障诊断研究[J].航空兵器，2010（2）：58-61.