智能旋翼基于陷波器的振动载荷抑制算法

周云 胡和平 张仕明

摘要：智能旋翼为直升机减振降噪提供了一条极具发展前途的技术途径。本文研究了一种用于智能旋翼减振的连续时域控制算法，该控制算法主要由陷波器和通道增益两部分组成，对每一个控制反馈通道，将产生两路状态信号，系统减振效果取决于两个状态通道增益的比值。控制仿真结果显示，该控制算法具有出色的减振效果，并对随机噪声和谐波千扰信号都具有较强的抑制作用，为了抑制4Ω旋翼桨毂振动载荷，所需的后缘襟翼控制量是3Ω/4Ω/5Ω多谐波组合输入。相较于经典的离散频域高阶谐波控制算法，该算法是一种连续時域控制算法，可大幅加快控制系统的收敛速度，与此同时，在非平稳的直升机飞行状态下，也具有更佳的减振效果。

关健词：智能旋翼;后缘襟翼;减振;陷波器;时域控制

中图分类号：V219 文献标识码：A

振动是目前直升机面临最棘手的问题之一，现役直升机普遍存在振动水平偏高的问题，而用户对新研直升机的振动水平技术指标又提出了越来越高的要求，对于下一代先进直升机，要求振动水平控制在0.05g以内[1]，现代直升机研制对减振技术需求极其迫切。近年来，随着智能材料与结构、主动控制等基础技术的发展，智能旋翼为直升机减振提供了一条极具发展前途的技术途径[1～3]，并成为当前直升机行业研究的一个热点。

智能旋翼根据驱动方式的不同有多种形式，包括单片桨叶控制（Individual Blade Control，IBC）、主动后缘襟翼（Active Controlled Flap，ACF）、主动扭转旋翼（Active TwistRotor，ATR）等构型，其中，基于压电陶瓷叠堆驱动的主动后缘襟翼智能旋翼最具工程应用前景[4～6]。2009年，由美国波音公司、美国国防预先研究计划局（DARPA）、美国国家航空航天局（NASA）、美国陆军联合研制的Smart Rotor，已完成全尺寸风洞试验验证，结果显示旋翼振动载荷降低了88.4%，桨涡干扰（Blade-Vortex Interaction，BVI）噪声降低了7dB[7，8]，2014年，德国航空航天研究院（DLR）研制的BluePulse智能旋翼在EC145平台上完成了飞行验证[9]，验证结果非常令人鼓舞。在国内，南京航空航天大学和中国直升机设计研究所等单位也在开展基于智能旋翼的减振降噪技术研究，但在减振的闭环控制算法方面大多采用了高阶谐波算法[10～12]，高阶谐波算法本质上是一种离散频域控制算法，它是基于旋翼转速周期来进行控制的，控制更新的速率较慢，导致控制系统收敛时间较长，同时也限制了它只适用于较平稳的飞行状态，且在控制更新时刻可能会出现控制信号的阶跃变化，容易对驱动器造成冲击损伤[13，14]。

根据直升机减振主要针对nQ谐波频率成分的特点，本文基于陷波器基本原理，研究了一种智能旋翼减振控制算法，它是一种连续时域控制算法，可大幅加快控制系统的收敛速度，与此同时，在非平稳的直升机飞行状态下，也具有更佳的控制效果。

1 控制算法

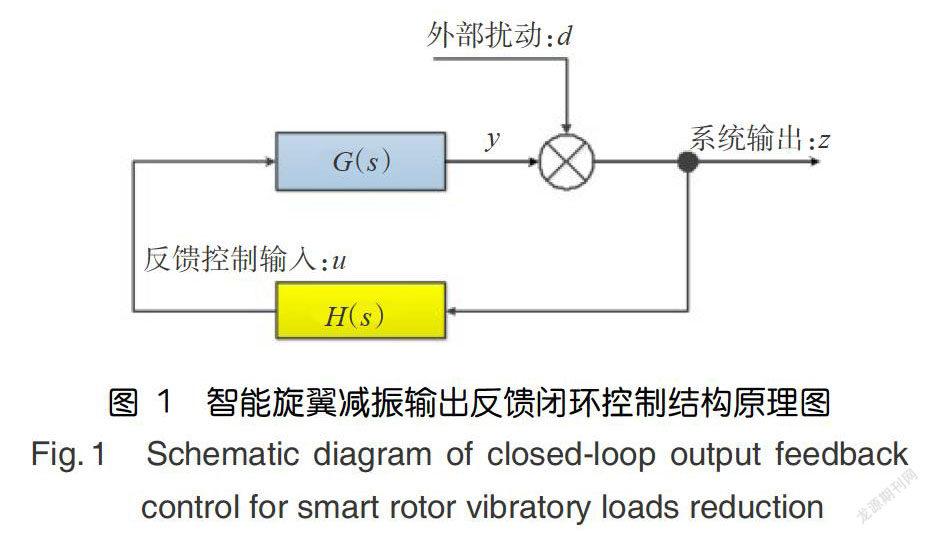
直升机振动响应具有显著的谐波特性，以旋翼通过频率nΩ谐波成分为主，因此智能旋翼减振目标就主要抑制nQ频率的旋翼振动载荷，图1是采用输出反馈闭环控制的智能旋翼振动载荷抑制系统原理图，其中，d（t）是由非定常气动力外载引起的基础旋翼振动载荷，G（s）是控制通道传递函数，z（t）是系统的输出响应H（s）就是反馈控制器，通过反馈控制信号u（t）驱动智能旋翼后缘襟翼动态偏转，进而产生一个附加的旋翼振动载荷增量y（t），进而实现对基础旋翼振动载荷的抵消或抑制。

1.1 控制通道频响矩阵

首先建立旋翼控制数学模型，得到控制通道的频响矩阵，旋翼减振的目标通常是不旋转坐标系的旋翼桨毂振动载荷或机身振动响应，因此采用不旋转系多桨叶坐标来描述旋翼控制模型具有更好的精度[6]，基于准定常假设，可以得到拉普拉斯域表达的旋翼控制模型：

z（s）=G（s）·u（s）+d（s）…（s=j·nΩ）（1）式中：z（s）为旋翼桨毂振动载荷输出;u（s）为控制输入d（s）为待抑制的基准桨毂振动载荷;G（s）为表征后缘襟翼控制输入到桨毂振动载荷输出关系的传递函数。

1.2 基于陷波器的旋翼振动载荷抑制算法

对于如图1所示的智能旋翼减振闭环控制系统，定义系统输出z相对于外部扰动d的灵敏度传递函数：

那么智能旋翼的减振效果就可以用函数S（s）来描述，为了使灵敏度函数S（s）在控制频带范围内幅值足够小，也就期望控制系统开环传递函数H（s）G（s）要尽量大，那么可以基于调谐陷波滤波器来设计反馈控制器H（s），陷波器传递函数形式如下：

它本质上是一个无阻尼的二阶共振系统，nΩ是系统共振频率，可以看出，当s=j·nΩ时，控制器处于共振状态，H（s）趋于无穷大，那么此时S（j·nΩ）=0，即共振频率点的谐波信号将被完全抑制。

下面根据陷波器原理来设计智能旋翼减振时域控制器，图2是控制算法核心部分原理图，主要由陷波器（NotchFilter）和静态增益（Static Gain）两部分组成。

首先，根据陷波器的传递函数形式，写出对应的时域状态空间方程表达式：

x=Ax+Bz

u=Cx+Dz（4）

其中状态矩阵表达式如下：

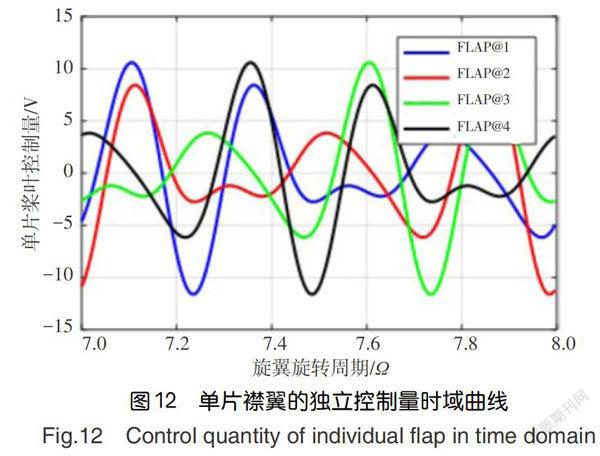
控制反馈信号z（t）进人控制器后，通过陷波器的作用，将得到两路状态变量，记为x=[x₁x₂]^T，其中x₂=x₁，因此，x₁为控制器状态变量，x₂为控制器状态微分变量，两路状态信号再分别通过静态增益c₁和c₂作用后，两部分线性组合形成控制信号u（t）。当反馈信号是频率为nΩ的谐波信号时，陷波器的两路状态变量信号x₁（t）和x₂（t）的幅值正好相差nΩ倍，且方向相互垂直，即X₂=x₁·（j·nΩ），且在共振频率nΩ处，状态变量x₁（t）相对于z（t）相角变化-90°，状态微分变量x₂（t）相对于z（t）相角变化0°，那么控制信号可以表示为：