基于动态网格的多体分离计算技术研究

徐琳 宋万强

摘要：多体分离问题是航空航天等工业设计部门非常关心的问题之一。目前，多体分离轨迹问题主要依托风洞试验和数值模拟两类。本文基于网格变形与局部重构相结合的动态网格方法，在单步小位移的情况下用Laplace算法进行网格变形.当总的位移量逐渐增大至网格质量低于设定标准时，进行局部网格重新生成，采用非结构网格、Euler方程、准定常的方法开展外挂投放数值求解，模拟了典型的多体分离标模（机翼/外挂物分离），并与AEDC风洞试验结果进行了对比，验证了本文多体分离计算技术的准确性。

关健词：动态网格;多体分离;数值模拟;网格变形;Laplace

中图分类号：V224.5 文献标识码：A

多体分离过程相当复杂，不同物体之间存在相互干扰，为确保飞行器的飞行安全，必须研究他们之间的干扰与分离，因此，多体分离问题是航空航天等工业设计部门非常关心的力学问题之一[1]。目前，多体分离轨迹问题主要依托风洞试验和数值模拟两类。风洞试验采用的技术方法主要有捕获轨迹系统（CTS）、自由投放试验、网格扫描方法和流向角方法等。总体来说，地面设备不足使得采用风洞试验手段研究多体分离问题相对比较困难，尤其是在高速机动飞行等非常规情况下，试验研究的局限性越发明显[2，3]。近年来，数值方法的进步使得仿真计算越来越能逼近现实状况，采用数值方法模拟多体分离轨迹也逐渐成为一种常用的技术手段[4]。

多个物体分离时各模型边界之间的相对运动幅度较大，这对于采用数值模拟方法进行分离轨迹求解的计算网格提出了更高的要求，也是其所需解决的关键问题。目前国内外比较成熟的动态网格求解技术大致可以分为三种。

（1）嵌套网格技术

嵌套网格技术由运动物体网格和背景网格组成，通过对重叠区插值运算完成网格间的数据传递计算。此类方法为国外常用的运动问题求解算法，相对成熟。其缺点是频繁的插值运算会带来解的精度损失。

（2）网格变形技术

随着模型相对位置的变化，计算网格会按照设定的变形算法进行压缩或拉伸变形，以保证网格与模型边界的贴合。常用算法有弹簧法、弹性体方法Delaunay图法和RBF网格变形方法等。此类方法多用于非结构网格，其缺点是当相对运动较大时，网格质量无法保证。

（3）网格重生技术

当模型相对位置发生变化时，网格依据新的模型重新生成，并通过插值将原网格的物理量传递给新的网格。此方法能保证求解过程中的网格质量，其缺点是频繁的插值运算会带来解的精度损失，且网格重生会耗时较长，影响效率[5]。

本文采用网格变形与局部重构相结合的动态网格方法：在单步小位移的情况下用Laplace[6，7]算法进行网格变形，当总的位移量逐渐增大至网格质量低于设定标准时，进行局部网格重新生成。采用这种动态网格方法可以计算一个或多个运动物体的轨迹。本文采用非结构网格、Euler方程、准定常的方法开展外挂投放数值求解，模拟了典型的多体分离标模（机翼/外挂物分离），并与阿诺德工程发展复杂综合体（AFDC）风洞试验结果183进行了对比。

1 轨迹计算方法

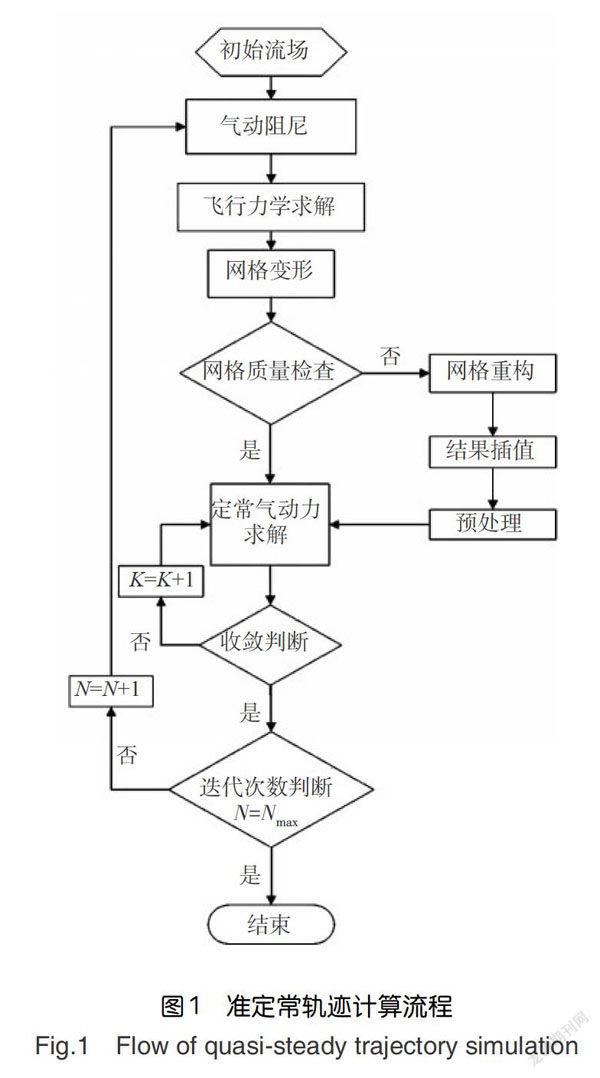
本文运用运动网格变形/局部重构计算的动态网格求解方法，对机翼外挂物分离轨迹进行数值模拟。具体的计算过程如图1所示。

具体为：（1）首先利用非结构网格生成技术生成背景网格和分离部件子网格，并设置网格变形及轨迹计算相关参数;（2）然后利用“挖洞”技术进行局部网格重构，生成背景网格与分离部件一体的初始计算网格，并计算定常流场作为初始流场;（3）由于计算的流场力为定常气动力，需增加气动阻尼进行运动物体受力修正;（4）求解六自由度方程，计算分离物体的下一位置和姿态;（5）移动分离物体，进行网格变形，进行网格质量检查，若网格质量不能满足计算要求，则利用“挖洞”技术进行局部网格重构，生成新的网格;（6）采用欧拉方程进行数值模拟，求取分离物体的受力分布;（7）判断气动力是否收敛，如果未收敛则继续进行内迭代，如果收敛则进行下一步;（8）重复（3）～（7）步，直至轨迹模拟求解结束。

2飞行力学模型

本文中使用到的飞行力学模型是建立在刚体六自由度运动基础上[9，10]，涉及到的运动方程如下所示：

L'_C=ω'I'_C+ω'×（ω'I'_C）

Ω'=ω'（4）式中：F为运动物体上的合力;m为指运动物体的质量;r_C（t）和r_C（t）为指速度及质心的位置;L_C为运动物体上相对于物体质心的合力矩;ω为角速度;I_C相对于运动物体质心的惯性张量;t为当前时间步;t⁰为上一个时间步;Ω为旋转角速度。上面的公式可以写为：

q=f（q）（6）式中：f是相对于右手坐标系。

A（5）、A（6）是运用五阶Runge-Kutta方法进行求解，这种方法在多体分离的求解中可以提供一个较高精度的解。在准定常求解中，每一个时刻的流场求解运动物体的运动都是定常的。为了把运动物体的运动影响加入计算结果中，本文在计算运动物体受力中增加气动阻尼：式中：C_lp，C_mq和C_nr为气动阻尼系数;P，Q和R为运动参考面内的滚转、俯仰和偏航速度;q_dynr为运动物体上的气动压力;S_r，c_r和b_r分别为运动物体的参考面积、参考弦长和参考展长。

3 网格变形/局部，构技术基本原理

本文采用网格变形与局部重构相结合的方法：在单步小位移的情况下用Laplace算法进行网格变形，当总的位移量逐渐增大至网格质量低于设定标准时，进行局部网格重新生成。在小位移的情況下，网格变形就是通过移动网格点的位置来贴合运动物体的边界。最常见的方法就是拉普拉斯光顺，使如式（8）所示的二次方程最小化：式中：δ为某一坐标方向的位移;n_i，j^ref为边矢量;I_i，j^ref为与该边矢量相关的对偶网格曲面矢量。这个二次方程最小化的求解是对位移场的每一项单独求解，也就是说忽略了不同坐标矢量之间的耦合。

式（9）为网格拉伸率P的定义。当网格没有负体积，且网格拉伸率ρ满足：ρ_min<ρ<ρ_max。其中，最小网格拉伸率ρ_max与最大网格拉伸率ρ_max为用户设定。当总的位移量逐渐增大至使网格质量低于设定标准时，进行局部网格重新生成。网格拉伸率P的定义如图2所示。

当通过网格变形得到新的网格质量无法满足要求时，则会进行局部网格重构，生成新的网格，再进行气动计算。局部网格重构是指根据用户定义的具体范围，对运动背景网格（多指机体网格）进行挖洞，将运动物体及其周围网格（多指弹体网格）根据运动物体运动位置填入机体网格，并将机体网格与弹体网格之间局部重构新的网格。具体流程为：（1）首先根据用户自定义的一个或者多个outer box对背景网格进行挖洞（outer box可以穿越壁面），保留用户定义的box外的网格;（2）根据用户定义的一个或多个innerbox，保留box内运动物体周围的网格，让其随运动物体一起运动（inner box不可以穿越壁面，需将运动物体全部包含在内，如果运动物体周围有加密网格，需将运动物体周围的加密网格包含在内）;（3）outer box之内inner box之外的部分生成新的网格;（4）最后将三部分网格合成新的网格，完成局部网格重构。如图3所示。

4 算例验证

4.1 二维双翼型算例

为了高效地验证本文轨迹计算的能力，方便直观地展示计算过程中的网格变形情况，本文首先采用二维双翼型算例。本次计算的二维双翼型算例是由两个NACA0012翼型构成，初始位置如图4（a）所示，上边的翼型充当飞机，下面的翼型充当导弹。本次计算来流马赫数为0.8，雷诺数为1.8×10⁷，下翼型重量（质量）5000kg，当地重力加速度为9.8m/s²，横摇阻尼系数取-4.0/rad，纵摇阻尼系数取-40.0/rad，偏航阻尼系数取-40.0/rad。流场求解采用欧拉方程准定常计算。

图4为双翼型轨迹模拟过程网格变形/重构图。图4（a）为采用非结构网格生成技术生成的背景网格以及运动物体子网格;图4（b）为初始位置网格，它是由背景网格和运动物体子网格通过上文所讲的局部网格重构技术生成的;图4（c）为小位移情况下，通过拉普拉斯光顺的方法进行网格变形，从图4（c）可以清楚地看出，下面的翼型上翼面网格被拉伸，下翼面网格被压缩;图4（d）为大变形情况下，网格变形已经不能满足计算对网格质量的要求，通过局部网格重构生成的该位置新的网格。图5为双翼型轨迹模拟过程压力分布云图。

4.2 AEDC算例计算

4.2.1 模型几何参数

AEDC外挂物标模算例的捕获轨迹系统（CTS）试验是由AEDC于1990年完成的。其模型，即机翼/挂架/带舵外挂物模型（Wing/Pylon/Finned-Store，WPSF）是美国发起第一次分离投放计算流体力学（CFD）验证时使用的一个机翼和导弹的简化模型[6]。如图6所示。很多研究都选用AEDC模型做为运动轨迹数值模拟的算例，是因为这个模型的几何数据和试验数据都比较详细。

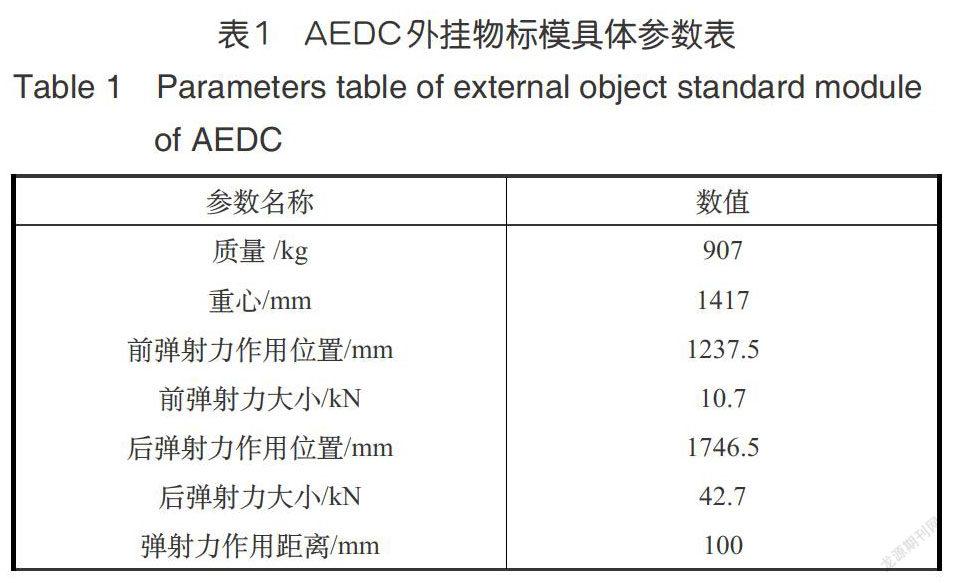
AEDC模型由一个带有双挂架的三角翼和一个简易导弹组成。其中，三角翼的展向截面为NACA-64A010翼型，机翼倾斜角为45°;机翼的挂架由一个对称的弧面一平面一弧面组合而成，挂架的顶端与三角翼前缘的距离为0.61m，其对称线与三角翼对称线的展向距离为3.3m;导弹由一个旋转体与4个对称尾翼组合而成，其旋转体的半径为0.25m，总长度为3.017m。导弹和挂架之间的初始距离为3.66cm。在导弹分离的前0.054s内，导弹质心前后分别受到两个大小为10.7kN和42.7kN的弹射力作用，直至0.054s后导弹离开挂架，作用力消失。表1为AEDC外挂物标模的其他具体参数。AEDC外挂物标模受力示意图如图7所示。

4.2.2 初始网格和流场参数

本次计算共准备两套网格：背景网格wing.grid和运动物体网格store.grid。这两套网格采用Pointwise绘制，其中wing.grid共包含131487个节点和787942个单元，store.grid共包含27891个节点和143945个单元，由于本次轨迹计算采用欧拉方程求解，故并没有绘制棱柱层进行加密，仅对导弹轨迹区域附近进行了网格局部加密。具体网格示意图如图8所示。

本次计算来流马赫数为0.95，单位雷诺数为7.874×10⁶，迎角为0°，飞行高度是8000m。流场求解采用欧拉方程准定常计算，时间步长△t为0.002s，求解总时长1s。

4.2.3 模拟结果

通过网格局部重构的方法生成的网格如图9所示，为了保证导弹分离过程中对导弹流体计算的准确性，需保证计算过程中导弹周围网格的疏密度，因此，在设置时，将导弹周围加密网格区域在inner box的范围内，如图9所示导弹周围的网格为导弹初始网格的保留。

初始时刻定常流场计算的压力（压强）分布如图10所示，由于流动是跨声速的，因此，在外挂物中部和尾部区域出现激波。由于吊舱和挂架很近，二者之间有较强的气动干扰，使这一区域的流动比较复杂。图11为质心位移与试验值的对比图。从图11可以看出，采用准定常流动计算方法，实现了AEDC机翼/导弹分离标准模型轨迹模拟，Is时间内导弹投放軌迹计算结果与风洞试验数据基本吻合。

5 结论

本文通过采用网格变形与局部重构相结合的网格变形技术，以NACA0012和AFDC为例，耦合求解Euler方程与六自由度方程，采用准定常的方法实现了机翼外挂物分离轨迹数值模拟，证明本文网格变形/局部网格重构方法有很好的实用性。AEDC仿真结果与试验值吻合较好，验证了本文多体分离计算方法的准确性。

参考文献

[1]唐志共，李彬，郑鸣，等.飞行器外挂投放数值模拟[J].空气动力学学报，2009，27（5）：592-596.

[2]曾铮，王剛，叶正寅.RBF整体网格变形技术与多体轨迹仿真[J]，空气动力学学报，2015，33（2）：170-177.

[3]Torsten B，Lars T.Time-accurate CFD approach to numericalsimulation of store separation trajectory prediction[R].AIAA2011-3958，2011.

[4]Mahmood T，Aizud M N，Zahir S.Aerodynamic effects of thestore release onthe roll attitude of a wing configuration[C]//Transonic Flight Proceedings of International BhurbanConference on Applied Sciences&Technology，Islamabad，Pakistan，2011.

[5]聂璐，向锦武，飞机外挂物投放安全性的参数影响分析阴.飞行力学，2011，29（2）：25-28.

[6]黄鹏飞.拉普拉斯加权聚类算法的研究[D].南京：南京航空航天大学，2009.

[7]胡勇全.基于自动生成控制点的拉普拉斯变形[D].大连：大连理工大学，2012.

[8]Elias E P，Spyridon D K.CID transonic store separationtrajectory predictions with comparison to wind tunnelinvestigations[J].International Journal of Engineering（UE），2010，3（6）：538-553.

[9]范立钦.飞机飞行力学研究工作的回顾与展望[J].飞行力学，1987（01）：18-25.

[10]方振平，陈万春，张曙光，等.航空飞行器飞行动力学[M].1版.北京：北京航空航天大学出版社，2005.