小学数学几何知识中的迁移与简单应用

易路

关键词：小学数学;几何学习;迁移

【中图分类号】G623.5    【文献标识码】A       【文章编号】1005-8877（2019）22-0113-01

数学学习中，迁移是一种重要的学习方式。即把需要学习的知识系统与已有的知识系统建立起联系，也就是学习新知识链接到旧知识。在小学数学教学中，几何知识是非常重要的学习板块，如何在几何学习中渗透迁移思想呢？本文将从两个方面进行探讨。

1.小学几何知识中迁移

（1）面积公式之间的迁移

第一，长方形面积公式迁移推导至平行四边形面积公式。

教学平行四边形的面积时，先让学生独立思考，计算出老师准备的平行四边形的面积。这时提醒可以用格子图。学生分享时，一般会呈现以下几种观点：

①数格子：学生通过数格子（不满一格算半格），直接得到面积大小;

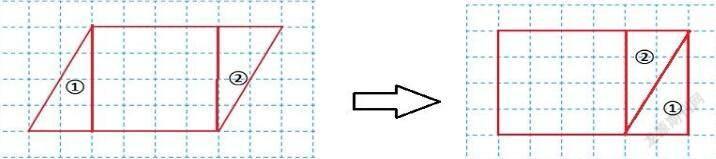
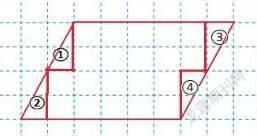
②拼凑组成长方形：如图所示，通过将①与②、③与④分别合成为完整的长方形，再计算出平行四边形的面积;

③平移：如图所示，通过平移①至图示位置，拼成了长方形。

此时利用长方形的面积公式推可导出平行四边形的面积公式：

长方形面积=长×宽  →   平行四边形面积=底×高

第二，平行四边形面积公式迁移至三角形、梯形面积公式。

①平行四边形面积公式迁移至三角形面积公式

教学三角形面积公式前，先引导学生复习平行四边形与三角形的关系（四年级下册有习题探讨了平行四边形与三角形的关系：两个完全一样的三角形可以拼成一个平行四边形）。让学生在拼一拼、剪一剪的活动中体会：平行四边形可以沿着对角线剪成两个完全一样的三角形。所以可以推导出：

平行四边形面积 =底×高  →  三角形面积=底×高÷2，实现了平行四边面积向三角形面积的迁移。

②平行四边形面积公式迁移至梯形面积公式

课堂上，引导学生仿照三角形与平行四边形的关系，是不是梯形与平行四边形也有类似的关系。学生通过自己动手操作可以得到，平行四边形也可以分成两个同样的梯形。但不同于三角形，平行四边形的底等于梯形的上底与下底的和（如图示）也就是：平行四边形面积= 底×高 → 梯形面积 =（上底+下底）×高÷2

（2）面积单位的构建迁移至体积单位构建

教学中，学习完“体积”的概念之后，立刻比较体积大小不连续的物体，如，冰箱与手机、大人与小孩的体积。然后抛出问题：怎样比较大小差不多的正方体和长方体的体积大小：

让学生回忆有遇到过类似的测量活动吗？引导学生回忆测量面积时，我们选用边长为一个长度单位（1cm、1dm、1m）的正方形做测量标准，让学生尝试类比遷移，测量体积我们该用什么做测量标准。在尝试中，学生可能会出现两种情况：沿用面积的测量标准，但测量的仍为面积（表面积）;或者用棱长为1个长度单位的正方体做测量标准。通过对比得到，应该采用棱长为1个长度单位（1cm、1dm、1m）的正方体做测量标准，实现了从面积单位向体积单位的知识迁移。

2.几何知识迁移的简单应用

（1）题型：在长方形中剪一个最大的正方形。

一个长方形长10厘米，宽4厘米，从这个长方形中剪下一个最大的正方形，这个正方形的边长是（  ），周长是（  ）。

（2）变式一：在梯形中剪一个最大的平行四边形。

在梯形中，剪去一个最大的平行四边形，求这个平行四边形的面积。

（3）变式二：在长方体中截取一个最大的正方体。

一个长方体长宽高为21、15、12，剪下一个最大的正方体，然后再切一次，求剩下的体积。

（4）思路：最大的正方形的边长为长方形的宽

迁移 → 最大的平行四边形的底为梯形的上底

迁移 → 最大的正方体的棱长为长方体中最短的棱长（宽或者高）

参考文献

[1]王丽燕.数学深度学习如何真实发生[J].湖南教育，2019（03）