五点二重有理逼近细分算法
朱 洪,王 娟,李宝萍
(安徽三联学院基础部,安徽合肥230601)
近年来,在计算机辅助几何设计或工业造型等领域,细分算法因具有处理简单、易于实现等优点而得到了广泛的应用,也基于此越来越多的专家和学者对其开展了广泛的研究,如Hassan等给出了C2连续的四点细分插值算法[1],Siddiqi等提出了一种具有C2连续的五点逼近细分算法[2],Tan等提出动态的三点二重逼近细分法[3]。根据不同的初始控制参数运用细分算法,可产生很多灵活的C3连续曲线。Akram等讨论了动态的插值四点细分法的保形性[4];Siddiqi等分析了C2连续的六点三重插值算法,并对其保凸性进行了具体的研究[5];Luo等基于逼近细分法去构造插值细分法[6];而檀结庆等则是从插值细分中给出逼近细分算法,并生成C2连续的极限曲线[7];Pan等把逼近插值两种细分算法相互结合,从而产生C2连续的细分曲线[8];王燕等分别给出了一类保凸的细分法以及含有两个形状控制参数的五点逼近细分算法[9-10];刘秀平等通过建立细分算法有关的矩阵,给出了插值细分曲线中有理参数点的求值[11]。将细分和样条这两种理论相融合也是曲线曲面造型中研究的重要工作,骆岩林等讨论了有理稳定细分方法,产生的曲线包括经常用的有理B-样条曲线[12];庄兴龙给出含有一个参数的五点二重逼近细分算法,并对该算法的连续性进行了分析[13]。基于以上研究,将有理B-样条曲线与逼近细分算法相结合,提出一种新的五点二重有理逼近细分算法,并在理论上证明该算法的一致收敛性和连续性,最后通过具体算例验证该细分算法的可行性及灵活性。
1 预备知识
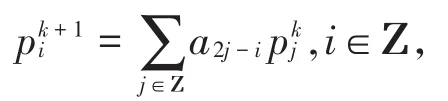

定理1[1]若二重细分法S一致收敛,则其掩模满足定理2[1]设二重细分法S的掩模满足定理1,则存在一个二重细分法S1,满足其中。同理,记Sn(n阶差分算法)的掩模为相应的生成多项式是
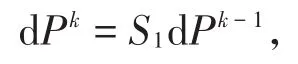
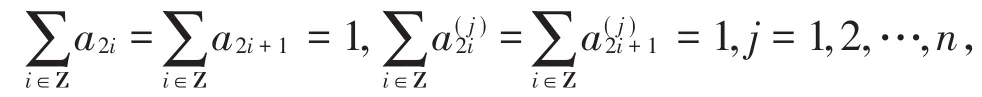
定理3[14]若二重细分法S的掩模和的掩模满足而且存在正整数L有成立,则由二重细分法S生成的曲线是Cn连续的。特别是取时
2 五点二重有理逼近细分算法和连续性分析
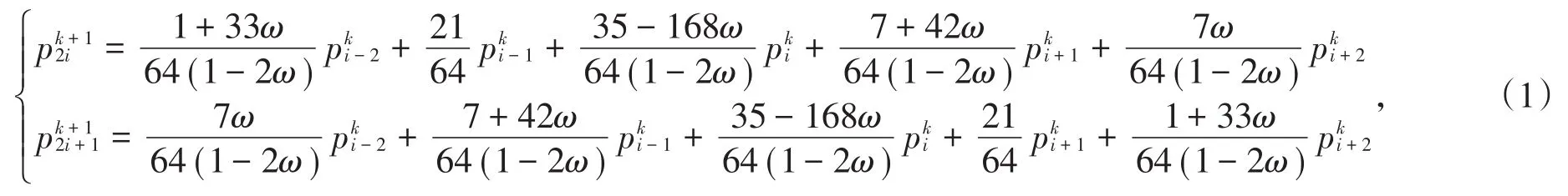

根据定理2,S1的生成多项式为
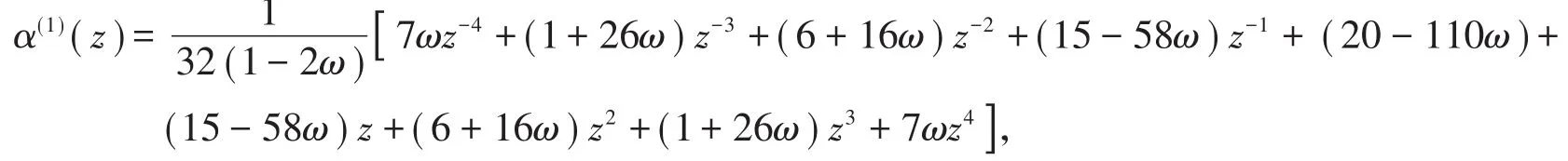
则有
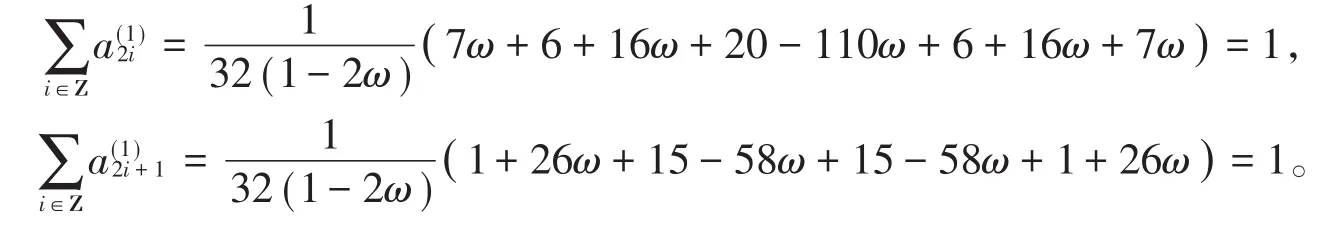

由定理3可知,五点二重有理逼近细分法一致收敛。
根据定理2,S2的生成多项式为
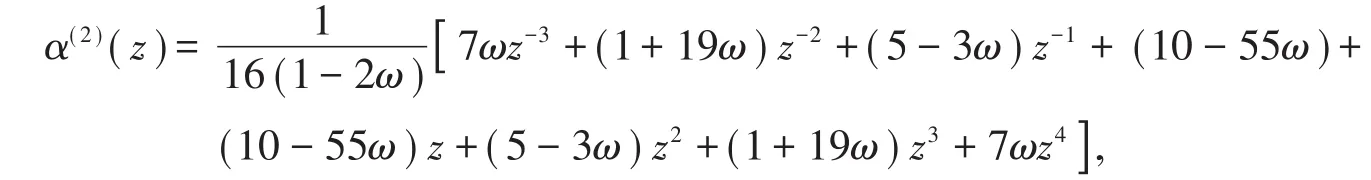
则有


由定理3知,五点二重有理逼近细分法C1连续。
证明 根据定理2,S3的生成多项式为
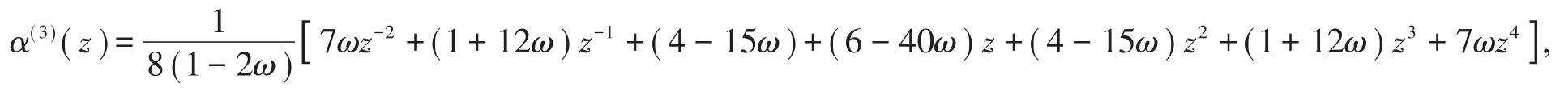
则有
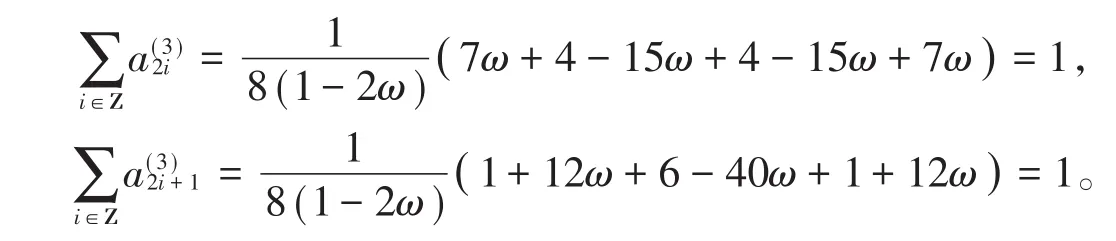

根据定理3知,五点二重有理逼近细分法C2连续。又根据定理2,S4的生成多项式为
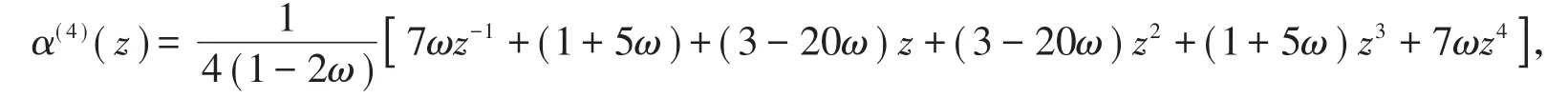
则有


根据定理3知,五点二重有理逼近细分法C3连续。
证明 根据定理2,S5和S6的生成多项式分别为
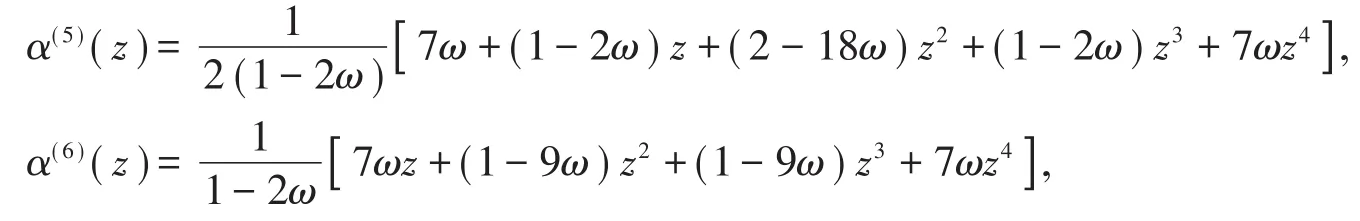
则有

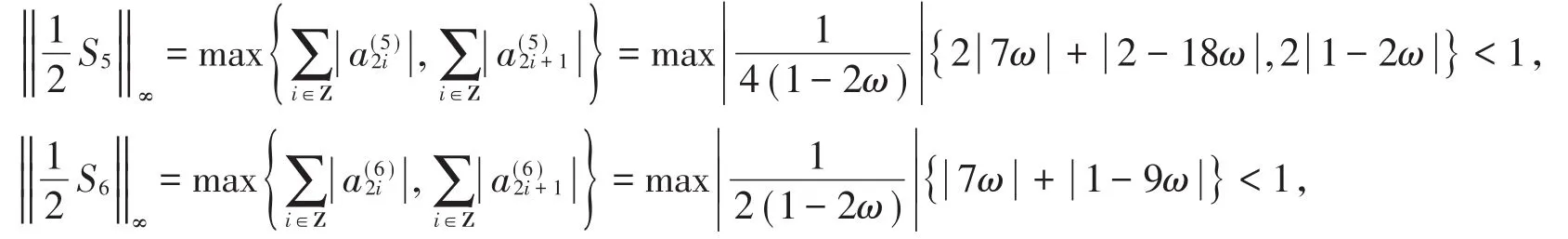
根据定理3知,五点二重有理逼近细分法C5连续。
根据定理3知,五点二重有理逼近细分法C7连续。
3 数值算例
根据连续性分析知,对于同一初始控制多边形,图1所示是参数ω=[-3/5,-7/20,0,1/30]的极限曲线变化动态图,它们分别为C1、C3、C5、C7连续。从图中可以看出,当参数从小到大变化时,极限曲线体现出越来越高的光滑度,而且比较贴近初始控制多边形,因此,这种有理逼近细分算法克服了传统逼近细分本身对初始控制多边形保持较弱的缺点。
当参数ω=-1/10时,对于同一控制多边形,细分算法(1)不同细分次数所生成的极限曲线如图2所示。在相同初始控制多边形下,当参数分别取时,极限曲线都保持着C3连续,但是随着参数取值的增大,极限曲线越来越靠拢初始控制多边形,如图3所示。比较细分算法(1)与文献[9]、[13]的算法,发现与文献[9]相比,在相同的连续性下,细分算法(1)的极限曲线更加接近控制多边形;与文献[13]相比,在相同的连续性下,细分算法(1)的参数取值范围较大,因此,对极限曲线的调控更加灵活,如图4所示。
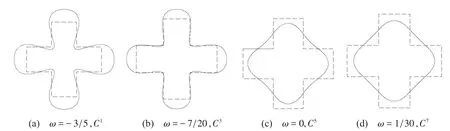
图1 极限曲线(虚线,初始控制多边形;实线,极限曲线)

图2 同一控制多边形的细分动态图
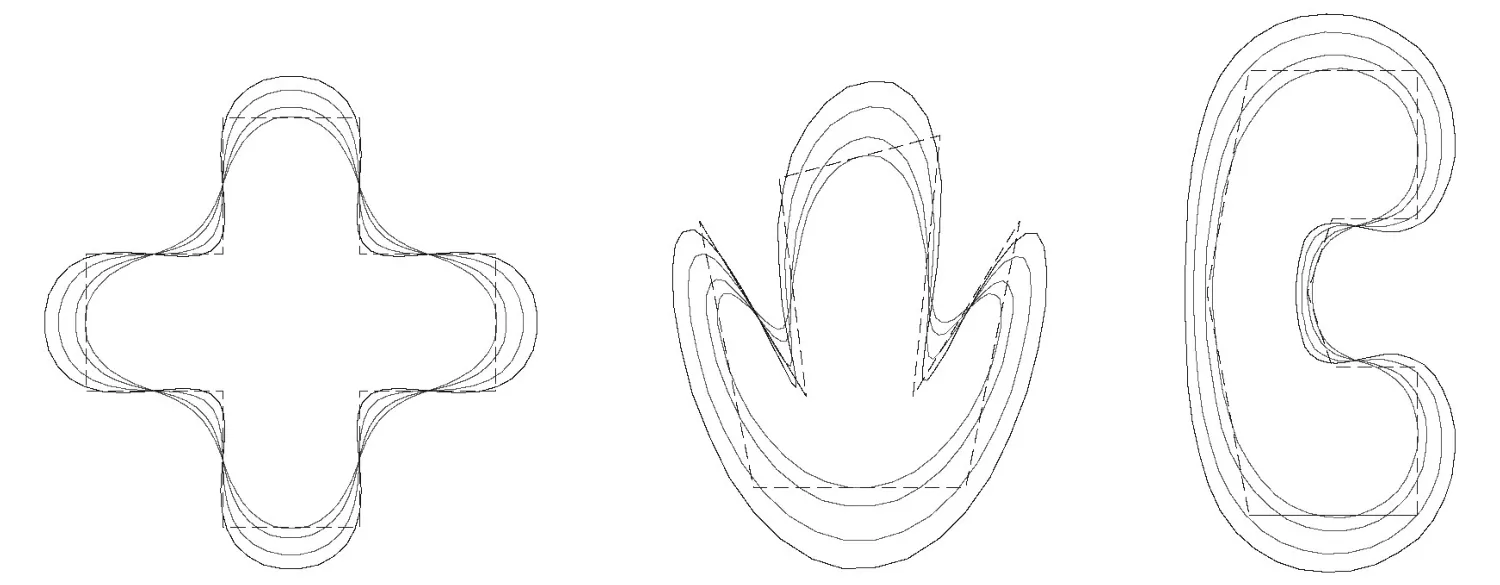
图3 极限曲线动态图ω=[-7/20,-1/4,-3/20,-1/10]
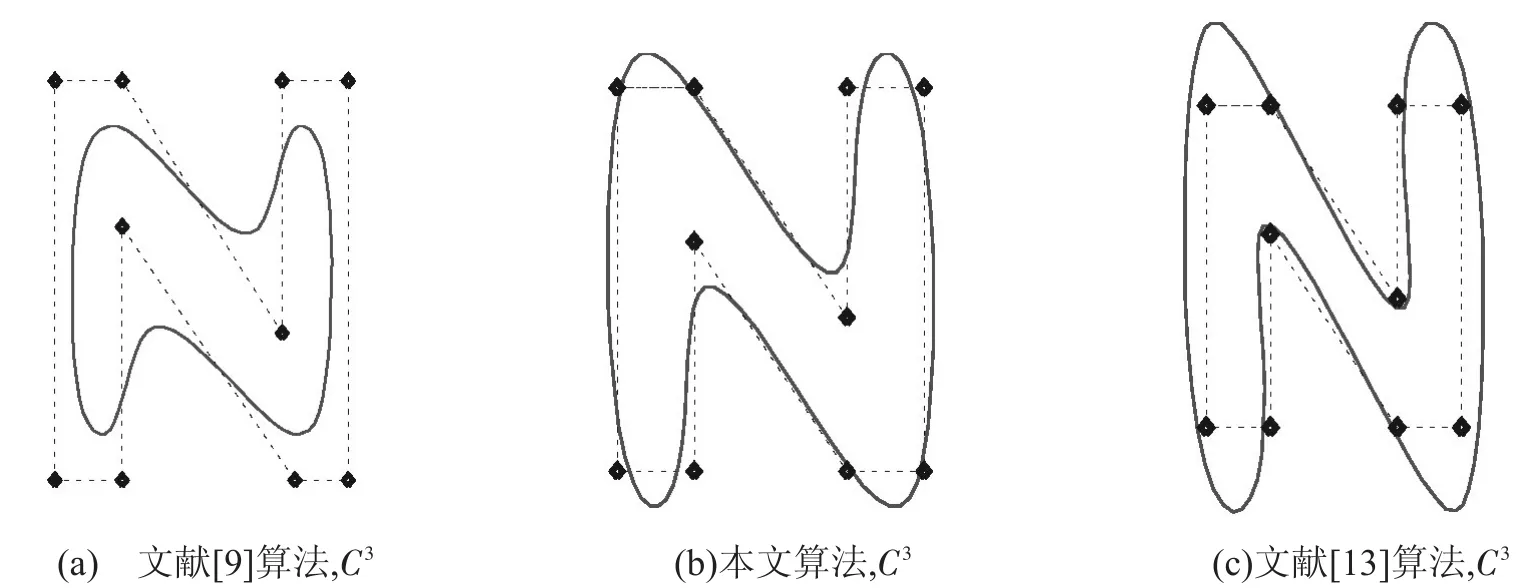
图4 算法对比(虚线:初始控制多边形;实线:极限曲线)
4 结束语
结合有理B样条曲线在工业造型设计中的应用,本文提出了五点二重有理逼近细分算法,使得生成的极限曲线除了保持较高的连续性以外,还能非常地接近初始控制多边形。未来工作将对该算法的保形性和多项式再生以及逼近阶等性质进行研究,从而更好地用于工业造型设计。

