迭代法在斜拉桥二次调索计算中的应用分析

李冠军

（广东省建筑科学研究院集团股份有限公司，广东 广州 510500）

斜拉桥是高次超静定结构，它对成桥线形有较严格的要求，每个节点坐标的变化都会影响结构内力的分配。桥梁线形一旦偏离设计值，势必导致主梁内力及索力偏离设计值。而主梁、桥塔和拉索之间刚度相差十分悬殊，受拉索垂度、温度变化、风力和日照温差、施工临时荷载、混凝土收缩徐变等复杂因素干扰，使力与变形的关系十分复杂。在施工计算中虽然可以采用多种方法，算出各施工阶段的索力和相应的梁体变形，但按理论计算所给出的索力、线形进行施工时，结构的实际变形却未必能达到预期的效果。这主要是由于设计时所采用的计算参数、施工临时荷载条件等与实际工程中所表现出来的不完全一致所引起的。斜拉桥在施工中所表现出来的这种理论与实际的偏差具有累积性，最终将会导致成桥后的索力、主梁内力和线形偏离设计目标。因此，除了在施工过程中严格控制各施工步骤、及时调整偏差以外，成桥后对达不到设计理想状态的索力进行二次调索，显得格外重要。

1 迭代法概述

二次调索的方法目前主要有迭代法和影响矩阵法[1]。影响矩阵法是将索力变量和其广义影响矩阵为目标函数，利用方程组得出各个索力的张拉值[2，3]。此方法较为快捷，但是无法考虑结构的非线性作用[4]。迭代法是通过迭代计算使误差的平方和最小，该方法可以考虑结构的非线性作用，对于大多数斜拉桥，一般迭代15次以内可以得到较合理的各索力张拉值[5]。

由于离塔端较远的索对塔和梁的变形影响较大，因此先调整靠近塔顶端附近的索就，即先调整长索能够减少总的调索量，从而可减少因二次调索引起的应力变化量。设第1次调整前，第i根拉索索力Ti0与目标索力Tim的差值为ΔTi0，第一次迭代，第i根拉索索力设置为Ti1=Ti0+ΔTi0，按照施工顺序进 行迭代计算，得出第一次第i根拉索的索力Tis1，其与目标索力差值为ΔTis1=Tig-Ti1，此时赋予第二次调整第i根拉索索力值为Ti2=Ti1+ΔTis1，再进行迭代，以此类推可知，第j次迭代值为Tij=Ti（j-1）+ΔTis（j-1），直至所有ΔTisj≈0，即可以得到最终各拉索的调整值[5]。

2 工程实例

2.1 工程概况

某斜拉桥为单塔单索面混凝土斜拉桥，采用塔、梁、墩固结体系。跨径组合为139 m+106 m。主梁高3.6 m，桥面以上塔高66.7 m，主桥宽33.5 m，为双向六车道，桥梁共设42对斜拉索。主桥下部主墩采用双肢薄壁墩配群桩基础，过渡墩采用柱墩配群桩基础。设计荷载为公路I级。桥梁立面图如图1所示。

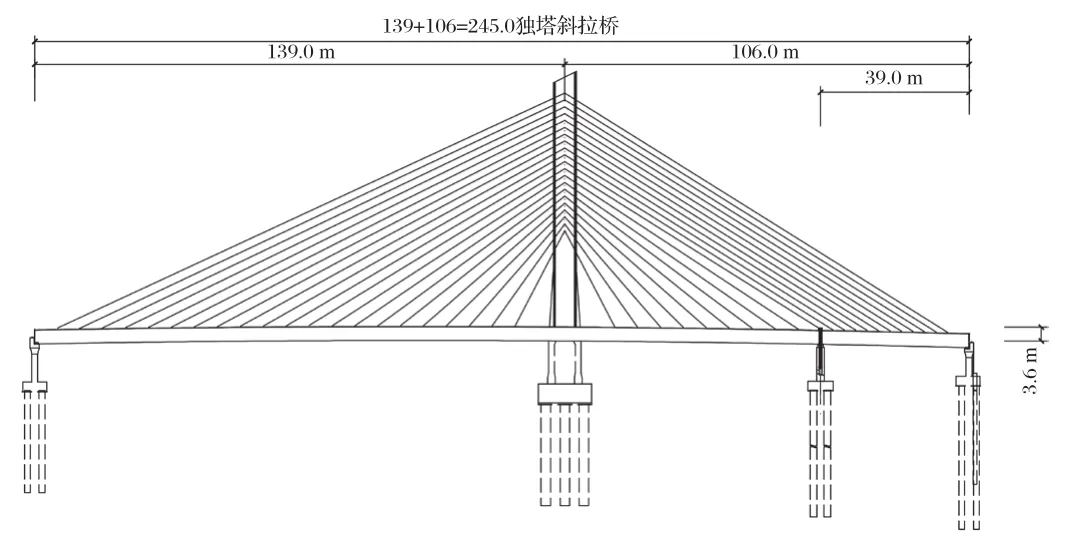
图1 桥梁立面图

2.2 建立有限元模型

利用有限元软件 MIDAS CIVIL建立全桥模型，梁、墩、塔用梁单元模拟，斜拉索用只受拉桁架单元模拟，并在施工过程中及时调整各悬臂施工阶段的参数，使有限元模型更加接近实际情况。全桥有限元模型图如图2所示。

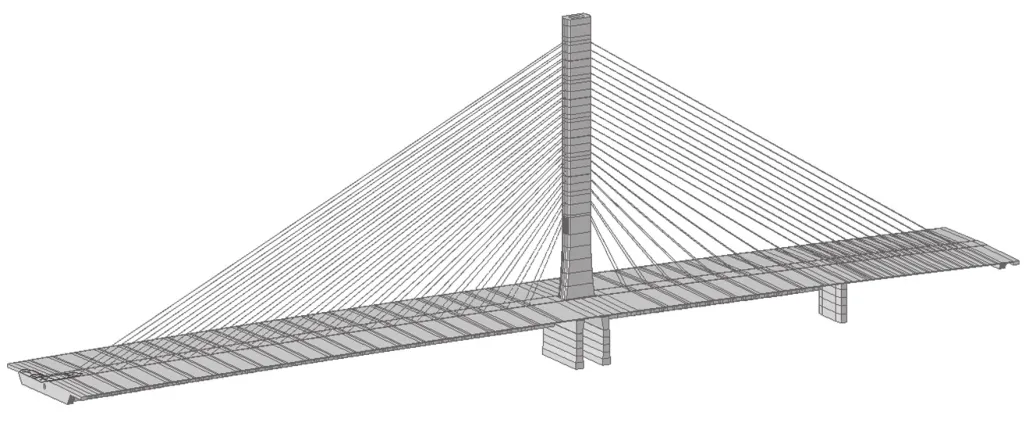
图2 有限元模型图

2.3 二次调索确定

本次二次调索是在桥梁合拢后，施工完桥面铺装后进行的调索。在该阶段，应以索力控制为主。根据调索前的索力实测值与目标索力，通过迭代法计算出各根斜拉索的索力张拉直，从长索向短索方向进行调整。具体各工况索力值如表1所示。由表1可见，调整后索力与目标索力偏差最大为3.2%，满足要求。

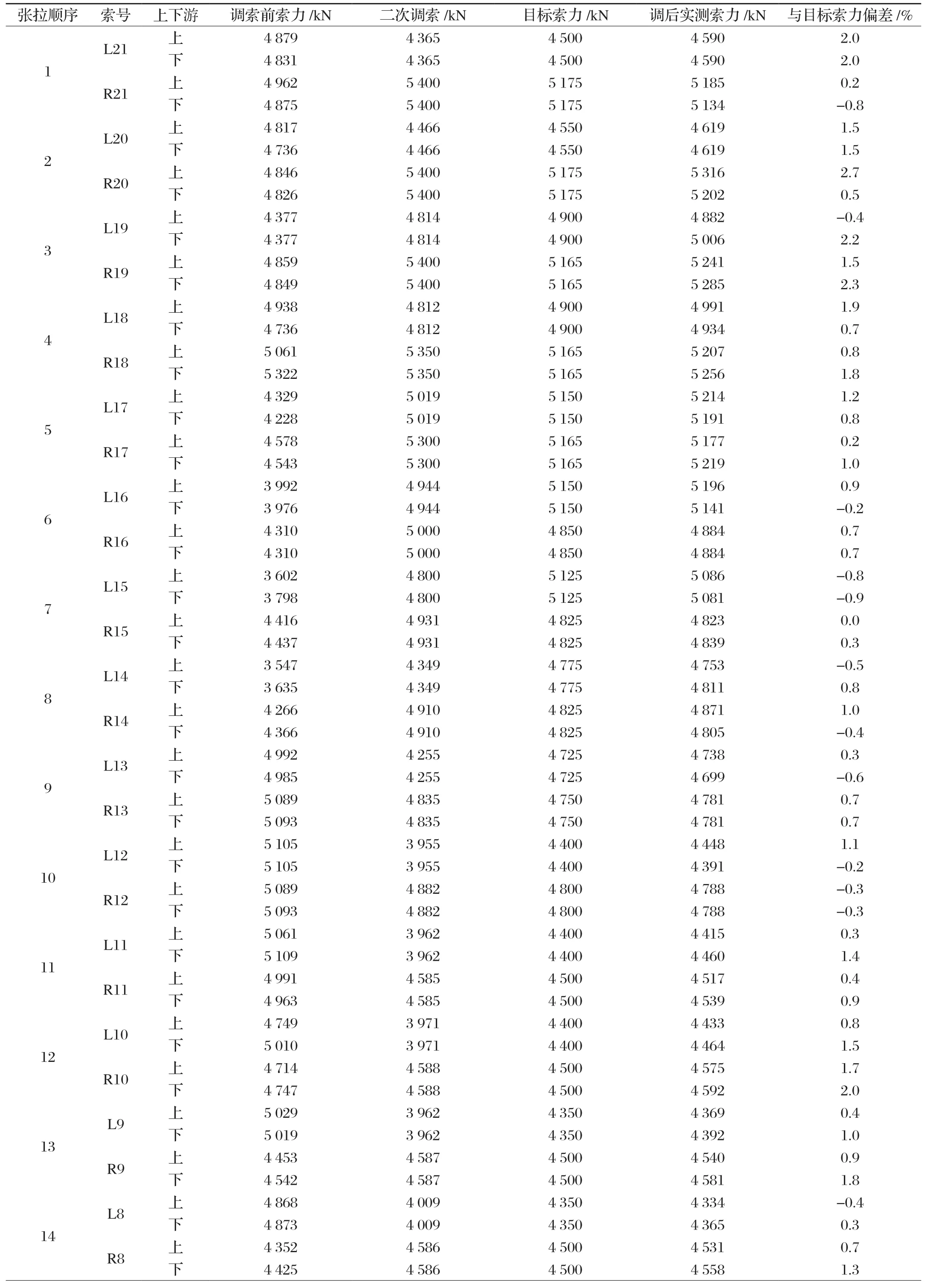
表1 二次调索索力值

续表1 二次调索索力值

2.4 二次调索后主梁应力

二次调索后，使得主梁上缘与下缘应力更趋合理，保证结构受力安全，如表2所示。

表2 主梁应力变化表 /MPa

3 结论

用迭代法计算斜拉桥二次调索索力值，计算简单快捷，控制目标明确，可较理想地达到设计成桥状态。结合某斜拉桥二次调索工程实例进行验证，通过迭代法计算二次调索可使斜拉桥达到较好的成桥索力状态，且可调节主梁应力局部过大的情况，使主梁受力更加合理，保证结构受力安全，同时也为桥梁后期运营和养护提供数据支撑。