从想象形状到精确度量，促进空间想象力深入发展——“运动的圆”之后的再思考和再实践

◇刘克臣

空间想象能力是指人们对客观事物的空间形式进行观察、分析和抽象的能力,是逻辑思维与几何知识及相关技能、经验的融合。培养学生的空间想象能力不仅是小学数学教学的重要内容,更是智力开发的一个重要方面。

2016年 11月，我在《小学教学（数学版）》发表了《站在运动的视角看图形,感受数学的神奇与美丽——以“运动的圆”为例》一文。在那次实践中，我将培养学生的空间想象力设为核心目标，主要让学生想象圆围绕正方形和正三角形滚动时圆心轨迹的样子，在此过程中突出了想象方法的指导。包括想象要真想，不能走形式和凭感觉，如果遇到困难，可以借助实践帮助想象。同时，突出了想象应该以知识为基础，凸显想象的准确与深刻。

这样的尝试有幸得到了东北师范大学史宁中教授的指导。史教授在充分肯定的同时，也提出了进一步思考的问题：想象出形状是培养学生空间想象力的重要内容，但是还不够深刻，如何再进一步？史教授的问题促使我深思：再向前，往哪儿走？

一 带着问题退回原点再思考

退回原点，需要思考的第一个问题是：什么是想象？

心理学中的想象是指人脑对已有表象进行加工改造、重新组合,产生新的综合性形象的心理过程。从心理学的解释看，想象是一种特殊的思维活动。它具有生动形象性和间接概括性的特点,强调在空间想象任务中的心理操作是其最重要的方面。解决空间任务时,将问题所描述的空间形象输入大脑暂时储存,而后大脑将进行一系列复杂的心理操作,使问题得以解决。

有学者认为，数学中的空间想象能力指的是人们对客观事物的空间形式进行观察、分析、抽象思考和构造创新的能力，即指对物体的形状、结构、大小、位置关系的想象能力。还有学者指出，空间想象力包括解释图形信息的能力和视觉加工能力。其中视觉加工能力,包括对视觉表征及视觉表象的操作和转换, 它是一种过程能力。其中，对视觉表象的操作和转换是建立在表象基础上的。

综合以上观点，用这样的视角回看“运动的圆”一课的实施过程，发现设计的学习活动主要聚焦于“想象出形状”，即强调学生在头脑中想象出物体运动轨迹的形状，没有进一步对想象出的形状继续加工。

第二个问题：想象力是否有水平和层次划分？

对于学生几何水平划分比较权威的是范希尔夫妇的划分方法。他们起初将学生的几何水平划分为视觉、分析、非形式化的演绎、形式化演绎和严密性五种水平，后来合并为直观水平、描述水平和理论水平。这样的划分虽然没有直接指向空间想象力，但是由于空间想象力是几何水平重要的组成部分，因此对空间想象力的培养具有重要指导意义。

国内有学者对空间想象力进行了水平划分。如任子朝等人提出：第一层次，空间观念的建立，包括实物的几何化，对空间基本图形的识记、再现和思考等；第二层次，建构几何表象的能力，即能在文字语言或直观支撑的刺激下,在大脑中想象出符合要求的图形的能力； 第三层次，几何表象的操作能力，这是指对头脑中建立的表象进行加工或操作以便建立新表象的能力,这里的表象可以是语言文字指导下的内部表象,也可以是直观图形刺激下的表象, 或者是二者的有机结合体。

基于国内外学者的研究，可以发现对想象出的形状进一步加工是培养空间想象能力的新的阶段。这一阶段将引领学生的想象不断深入，凸显数学的严密性和逻辑性。

二 “想象出形状”后继续研究什么

有了进一步研究的基础，接下来就是设计具体的教学活动。学生通过想象、实践与分析，已经知道了圆围绕正方形和正三角形以及任意正多边形滚动时圆心轨迹的形状（如图1）。

图1

还能继续研究什么呢？最好的办法就是进行学生调研。通过学生访谈，发现有学生基于思维习惯提出研究面积，但大部分学生第一反应都是想知道轨迹的长度到底是多少，看来这是顺应学生学习需求的一个自然问题。

学生能研究这个问题吗？首先，学生已经建立周长的概念，并且掌握了长方形、正方形以及圆的周长的计算方法。虽然图1中的这些图形没有直接计算的方法，但是借助学生原有的经验应该可以解决。

其次，解决这个问题和培养学生的空间想象力有什么关系呢？进一步思考后发现，要想优化解决这个问题，最好的方法是将图形“打乱”后重组，将现有图形进行加工产生一个新图形，这正是培养学生空间想象能力的新目标。解决这个问题既满足了学生的需求，又顺应了教学目标的发展需求。

三 在度量中促进空间想象力的深入发展

（一）铺垫蕴伏——看似平淡，另有玄机。

上课伊始，老师首先抛出下面的问题：下图中圆的周长各是多少（如图2）？

图2

这是一个常规问题，非常容易解决。紧接着，两个圆位置移动后紧贴在一起（如图3），提出新问题：如果小圆围绕大圆滚动一周，圆心轨迹的周长是多少？这样就和上节课的内容进行了对接。

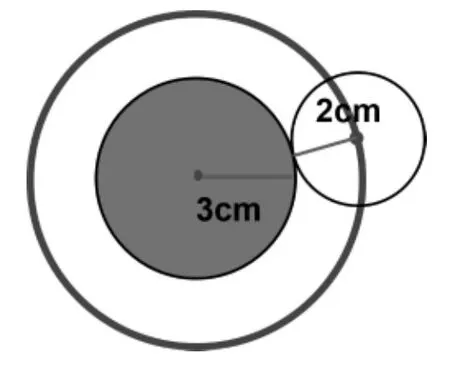
图3

学生解决这个问题主要有下面两种方法：

方法1：轨迹是个圆。

3+2=5(cm)

2×5×3.14=31.4（cm）

方法2：利用半径和周长之间的倍数关系。

是否还有别的方法呢？课堂上教师没有追问，希望学生在自然中发展。

（二）问题重现——二次想象，图形重构。

课堂教学的第二个环节，教师继续呈现学生上节课已经解决的问题，同时给出数据：圆的半径是2 厘米，正方形边长是4 厘米。圆心轨迹有多长（如图4）？

图4

学生主要的做法是把各部分累加，先求出一个小扇形弧的长度然后乘4，再加上4 条直边的长度。有的学生是用圆的周长加上正方形周长：4×4+2×2×3.14=16+12.56=28.56（cm）。他们的想法如图5所示：

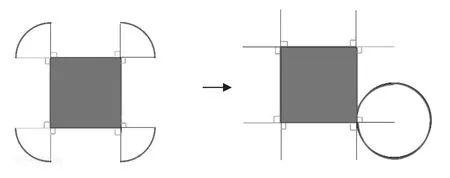
图5

有了度量周长的需求，促使学生不仅仅是将想象停留在想出形状上，而是将这个图形进行加工，把圆角矩形（如图4）转化为一个圆和一个正方形。这个过程不仅解决了周长的计算问题，更重要的是借助二次想象加深了对图形结构的认识。

圆围绕正方形滚动时圆心轨迹周长的问题对于学生仅仅是个热身，真正的挑战是圆围绕等边三角形滚动时圆心轨迹的计算问题（如图6）。

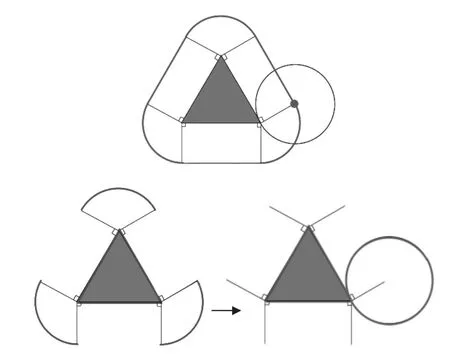
图6

学生能够借助前面的经验，想象出三条直的边可以组成三角形，但是对于三个扇形能否拼成一个圆产生了争议。经过讨论，学生发现每个扇形的圆心角都是120 度，这样是可以拼成一个圆的。因此，这个圆心轨迹也可以用三角形的周长加上圆的周长。

（三）经验推广——主动想象，形成体系。

课堂教学到这个环节时，每次都会有学生激动地提出：“是不是围绕什么图形滚动，轨迹都是这个多边形的周长加上圆的周长？” 受知识的影响，学生继续研究下去是有困难的，但问题研究到这儿教学目标已经达成。在学生火热的思考中，教师顺势再现课始的问题（如图3）：如果小圆围绕大圆滚动一周，圆心轨迹的周长是多少？

“哦！ 知道了！” 教室里立刻发出恍然大悟之声！学生发现，小圆运动一周后圆心轨迹的周长还可以是两个圆的周长相加。此时，这个圆形轨迹在学生眼中已经由一个大圆变形成了两个小圆。

通过这个环节的学习，学生将原本孤立的知识串联到一起，形成了一个完整的知识系统（如图7）。虽然还会有学生对圆围绕多边形滚动的问题有疑问，但相信这一连串的问题定会深深地印在学生头脑中，今后一旦有机会遇到，此时的经验会发挥积极的促进作用。

图7

（四）拓展空间——近在眼前，远在天涯。

借助具体形象的支撑，学生对想象出的图形进一步加工，对更大空间的想象是培养学生空间想象力的目标。教学最后环节，老师将空间进一步放大，呈现了下面这个经典问题：

假设在地球表面沿赤道贴着一条收紧的绳子。如果你把这根绳子放松2 米，并使之脱离地球表面，它将离地球表面大约多高呢？

依据经验和想象，学生会认为地球一周那么长，松开2 米后距离地球表面的具体变化会微乎其微。这样的想象对于任何人来讲都是十分困难的。教师引导：能否把这个问题转化为今天的学习内容？（图略）

学生发现，小圆的半径就是与地面的距离，原来地球表面（看成圆）的周长加小圆的周长就是轨迹的长度。小圆的周长是2 米，计算出半径大约是0.3 米，也就是与地面的距离，这个高度可以钻过一个人。这样的结果和学生的经验相距甚远，让学生体会到利用数学的精确计算可以使想象更加深刻，这就是数学的魅力。

面对史教授的追问，不知这样做是否就是最理想的过程。但起码在原有的基础上，将空间想象力的培养向前推进了一步。当然，空间想象力的培养是一个漫长的过程，绝不是借助几个活动就能完成的。小学阶段以培养学生空间观念为主，利用度量促进学生深入的想象，使学生的想象从直觉进入理性，是培养学生空间想象力的一个重要的阶段。我们期待在学生感受图形运动带来神奇与美丽的同时，使他们真正感受到数学的理性之美！