点云密度对水下抛石效果评价的不确定性研究

高 云 云1,，鲁 程 鹏1，王 茂 枚，姜 果，赵 钢

(1.河海大学 水文水资源学院，江苏 南京 210098； 2.江苏省水利科学研究院，江苏 南京 210017)

水下抛石效果评价是抛石护岸工程验收工作的重要部分，对水下抛石工程质量评价有重要意义。此外，水下抛石属于隐蔽工程，护岸段及其岸坡主要为第四系松散堆积物，极易冲刷流失[1-2]，应更重视水下抛石的施工质量检验。目前评价的重要指标是测点增厚值合格率和断面增厚值合格率，按照顺水流方向20～50 m一个断面，每个断面5～10 m测一个点进行合格率计算[3-4]。对具有隐蔽特性的水下抛石工程而言，第三方的监理评价决定着工程是否能够被验收。在实际工作中，为减轻工作量，常采用40 m一个断面进行评价，断面的选取对最终评价结果有着显著的影响，从而导致工程的监理作用大打折扣，不利于发挥工程的实际效益[5]。随着现代电子、计算机、信号处理技术的发展，多波束测深技术发生了质的飞跃，具有高精度、高密度、高效率和全覆盖的特点，逐渐被用于河道水下地形测量，精度可达0.1 m[6-7]。此时如仍沿用以往的验收标准，既不能对实际抛投状况进行客观全面的评价，还浪费了检验工作所耗费的物力和财力。但多波束测探技术所获得的数据点云密度一般过小[8]，实际工作中对精度的要求不高，因此有必要探讨一种适合抛石效果评价的点云密度，为工程质量检验评价提供依据。

本文以张家港市老海坝河段整治工程中的抛石护岸工程区为研究区，首先，在CARIS软件上根据施工期间获得的多波束水深点云数据分别导出不同密度的点云数据；然后，对不同施工区域前后两期数据进行叠加处理获取抛石增厚值，并分析不同点云密度对抛石效果评价的影响；最后，引入测量不确定度的概念对抛石效果评价指标进行不确定性分析。

1 资料与方法

1.1 研究区概况

研究区位于张家港市老海坝河段，是长江下游澄通河段重要的河势控制节点，也是重要的深水航道码头集中区。近几十年来，受如皋中汊和浏海沙水道汇流顶冲影响，河势变化剧烈，坍岸严重，经抛石治理，现河势已基本稳定。但近岸处深槽不断冲刷，出现多个水深50～70 m的冲刷坑，离岸距离仅150 m，严重威胁河势的稳定和近岸工矿企业的防洪安全。为维护老海坝河段河势和航道稳定，保障沿线码头运行安全，自2014年开始进行节点整治工程，于2016年完工并验收。验收评价时关于抛石增厚值的重要指标是固定断面增厚率，由于该指标是每隔20～40 m选择一个断面进行采样，故断面的选取情况对评价结果的影响较大[5]。

1.2 数据来源

数据来源于节点整治工程二期3个标段在施工期间(非汛期)的多波束水深数据，在施工期间共进行7次测量，从相邻测次间施工区域中分散性地选取12块50 m×100 m的区域，然后分别按0.5，1，2，3，4，5，6，7，8，9 m和10 m的密度输出施工前和施工后对应日期测次的多波束点云数据，并对每块区域施工前后的两期数据进行叠加分析(利用ArcGIS平台)，得到每个区域在施工前后不同点云密度下的水深变化值，即测点增厚值。

1.3 分析方法

1.3.1增厚值的统计分析

根据DB32/T2334.2-2013《水利工程施工质量检验与评定标准》[4]，测点增厚值大于设计值75%的点为合格点，水深流急区可放宽至大于70%。为提高工作效率，避免选取固定断面使高密度点云数据在不同软件中切换，根据相关文献[9]，将合格点个数占总个数的百分比定义为测点合格率，所有测点增厚值的平均值定义为平均增厚值，所有测点增厚值的分布形态采用偏度和峰度来体现。利用统计分析软件(SPSS)计算所有区域不同点云密度下增厚值的统计特征值和评价结果，如偏度、峰度、测点合格率、平均增厚值等。

1.3.2误差分析

根据施工设计，研究区内抛石石块的粒径范围在0.16～0.65 m之间，认为0.5 m的点云密度下评价结果接近或等于真实值，这也是多波束测量系统可获取的点云密度。故将该点云密度下的测点合格率和平均增厚值作为参考值，用于分析其他点云密度评价结果的优劣程度。为统一分析所有区域不同点云密度下评价结果的优劣，取测量学中相对误差的概念[10-11],计算公式如下：

(1)

式中，δi定义为不同点云密度下的测点合格率相对误差(为了得出误差正负，不取绝对值)；b为0.5 m的点云密度下测点合格率；bi为其他点云密度下测点合格率；i取1，2，3，4，5，6，7，8，9，10(平均增厚值相对误差的计算同理)。

1.3.3不确定性分析

测量不确定度在1993年发布的《测量不确定度表示指南》中被首次提出[12]，它是一个与测量结果相关联的参数，表征合理赋予的被测量值的分散性，并反映了不同概率水平下可能的误差分布范围。测量不确定度分为2类：标准不确定度和扩展不确定度[13-14]。当误差分布为正态分布时，对于某一次测量i的标准不确定度为uc(即标准偏差)，则其真值Zi落在(Zi-uc,Zi+uc)的可能性为68.26%，即置信概率为68.26%时测量结果的置信范围为(Zi-uc，Zi+uc)。同理，其扩展不确定度为2uc或3uc时，置信概率则分别为95.40%和99.73%。

据此，对相对误差引入测量不确定度的概念，并利用SPSS软件进行检验，若通过正态分布假设，则可计算其在不同概率水平下相对误差可能的误差分布范围[15]。最后利用公式(1)反推不同概率水平下评价结果的置信范围，具体见公式(2)。

(2)

式中，δmax，δmin分别为相对误差的最大值、最小值；bmax，bmin分别为测量结果的可能最大值和最小值；bi为评价采用点云密度下的评价结果。

2 结果与分析

2.1 点云密度对增厚值空间分布的影响

为分析不同点云密度对增厚值空间分布的影响，选取增厚值分布不均匀的区域并分别对0.5，1，5 m和10 m的点云密度下的增厚值进行分析。由于不同点云密度下点的密度不一，不能直观观察到空间分布的区别，故对数据点云进行克里克金插值处理[16-17]，对比分析不同点云密度下的增厚值分布情况，结果见图1，对所有区域不同点云密度下增厚值的偏度和峰度作箱式图，见图2～3。在箱图中，最上方、最下方的粗线分别代表最大值、最小值，箱子的上边缘、下边缘和中间线分别代表上四分位数、下四分位数和中位数，最上方和最下方的星号表示样本数据中的极端值[18]。

结果初步表明：① 当点云密度为1 m时，抛石增厚值的分布和0.5 m点云密度下的分布并无明显差异，细节部分也能精确展现；当点云密度为5 m时，增厚值的分布趋势和0.5 m点云密度下相同，但局部地方的分布形态发生变化；当点云密度达到10 m时，增厚值的分布已基本不能体现，大部分区域的增厚值发生变化，说明此时增厚值的分布形态已发生明显变化，已不能作为最终评价的基础数据。② 点云密度的变化对反映增厚值分布形态系数(偏度和峰度)的影响并不显著，符合工作实际情况和概率论相关理论。

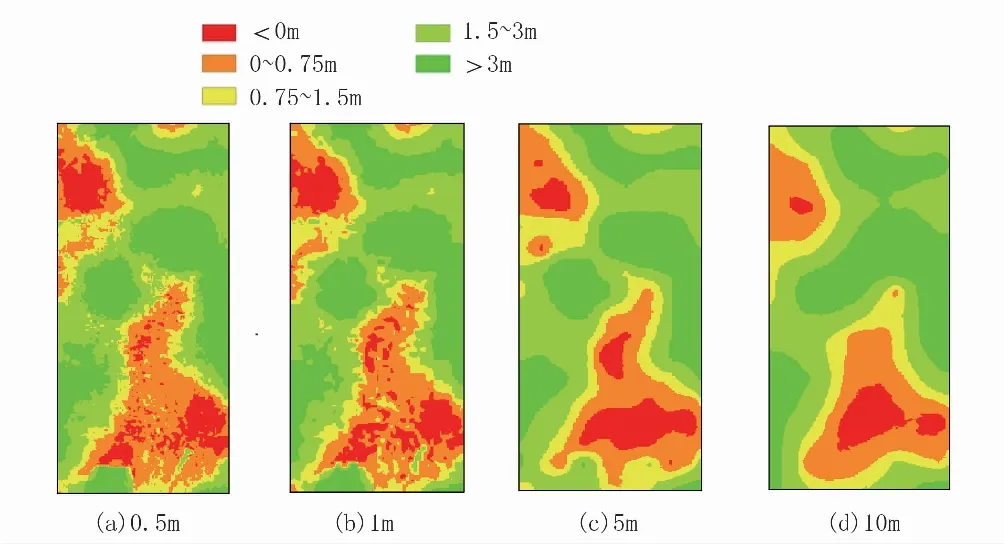
图1 不同点云密度下增厚值空间分布Fig.1 Spatial distribution of thickening values at different point cloud densities

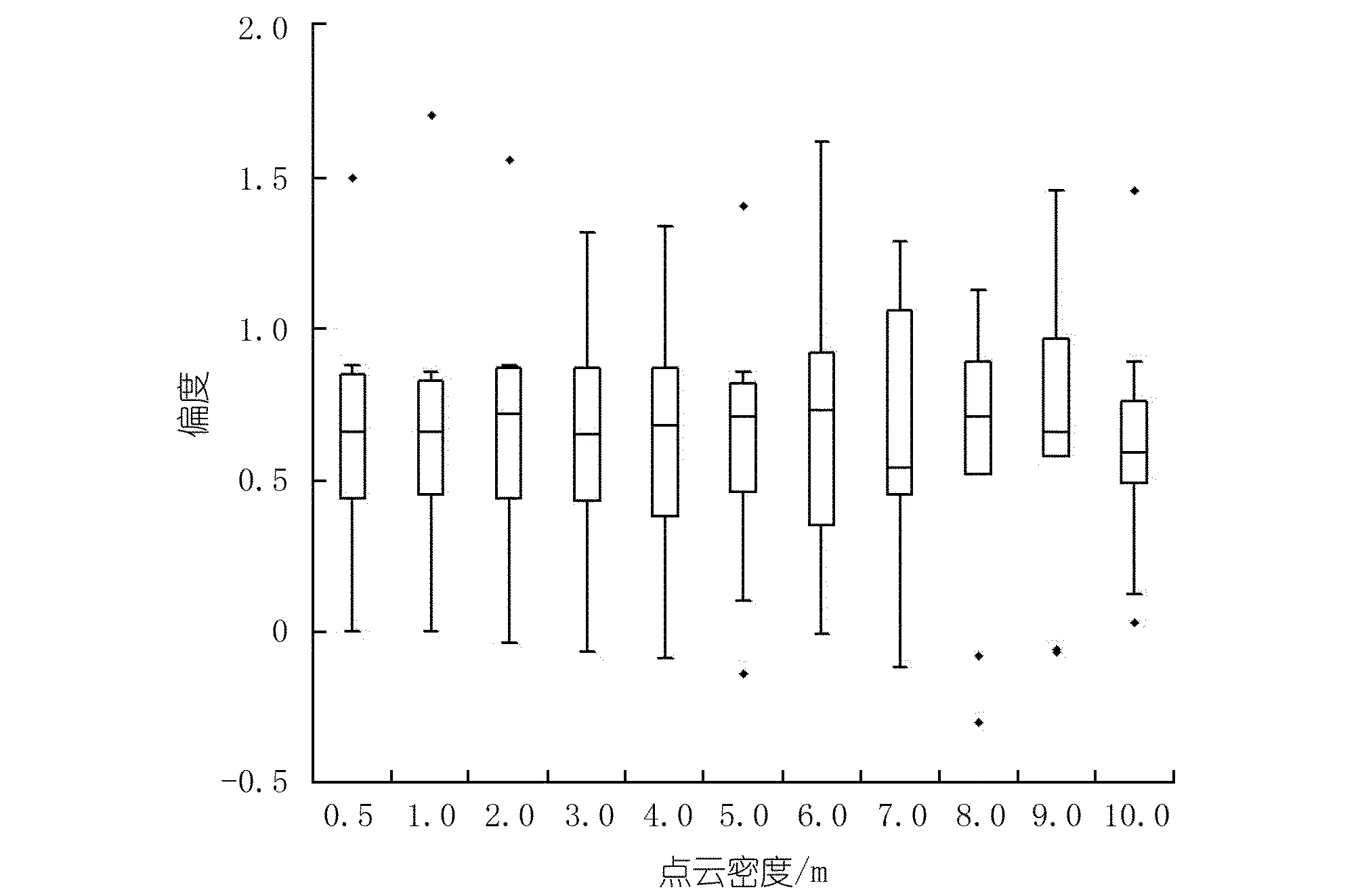
图2 不同点云密度下偏度分布箱式图Fig.2 Box diagram of deviation distribution under different cloud densities

图3 不同点云密度下峰度分布箱式图Fig.3 Box diagram of kurtosis distribution under different cloud densities

2.2 点云密度对评价结果的影响

根据公式(1)，计算不同点云密度下测点合格率和平均增厚值的相对误差，并对相对误差作箱式图，得出不同点云密度下相对误差的分布情况，见图4～5。结果表明：① 当点云密度为1 m时，两者的相对误差均分布在±2%之间，可作为精确评价分析时的点云密度；② 当点云密度小于5 m时，测点合格率和平均增厚值均逐渐增加；③ 点云密度大于5 m时，测点合格率和平均增厚值的相对误差分布范围逐渐稳定，大部分数据均分布在±8%之间，但其离散趋势有所增加；④ 该图证实了点云密度越小结果越精确的普遍规律，结果具备普适性。

图4 不同点云密度下测点合格率的相对误差分布箱式图Fig.4 Relative error distribution box plot of qualified points under different point cloud densities

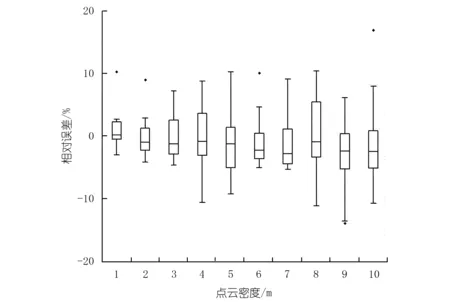
图5 不同点云密度下平均增厚值的相对误差分布箱式图Fig.5 Relative error distribution box plot of average thickening values under different point cloud densities

2.3 点云密度对评价结果的不确定性影响

2.3.1假设检验

由于实际工作以合格率作为验收标准，现对不同点云密度下的测点合格率的相对误差引入测量不确定度的概念，利用统计分析软件(SPSS)对其进行正态分布检验，结果见表1。由表1可知：除个别情况外，在显著性水平为0.05时，不同点云密度下测点合格率的相对误差均呈正态分布，符合自然界误差呈正态分布的规律；随着点云密度的增加，标准偏差呈现明显的增加趋势，平均值则先减小后增大。

2.3.2不确定性分析

由上节可知，增厚值合格率的相对误差呈正态分布，引入测量不确定度的概念，依据1.3.3节的方法计算不同概率水平下合格率的可能范围，结果见图6。

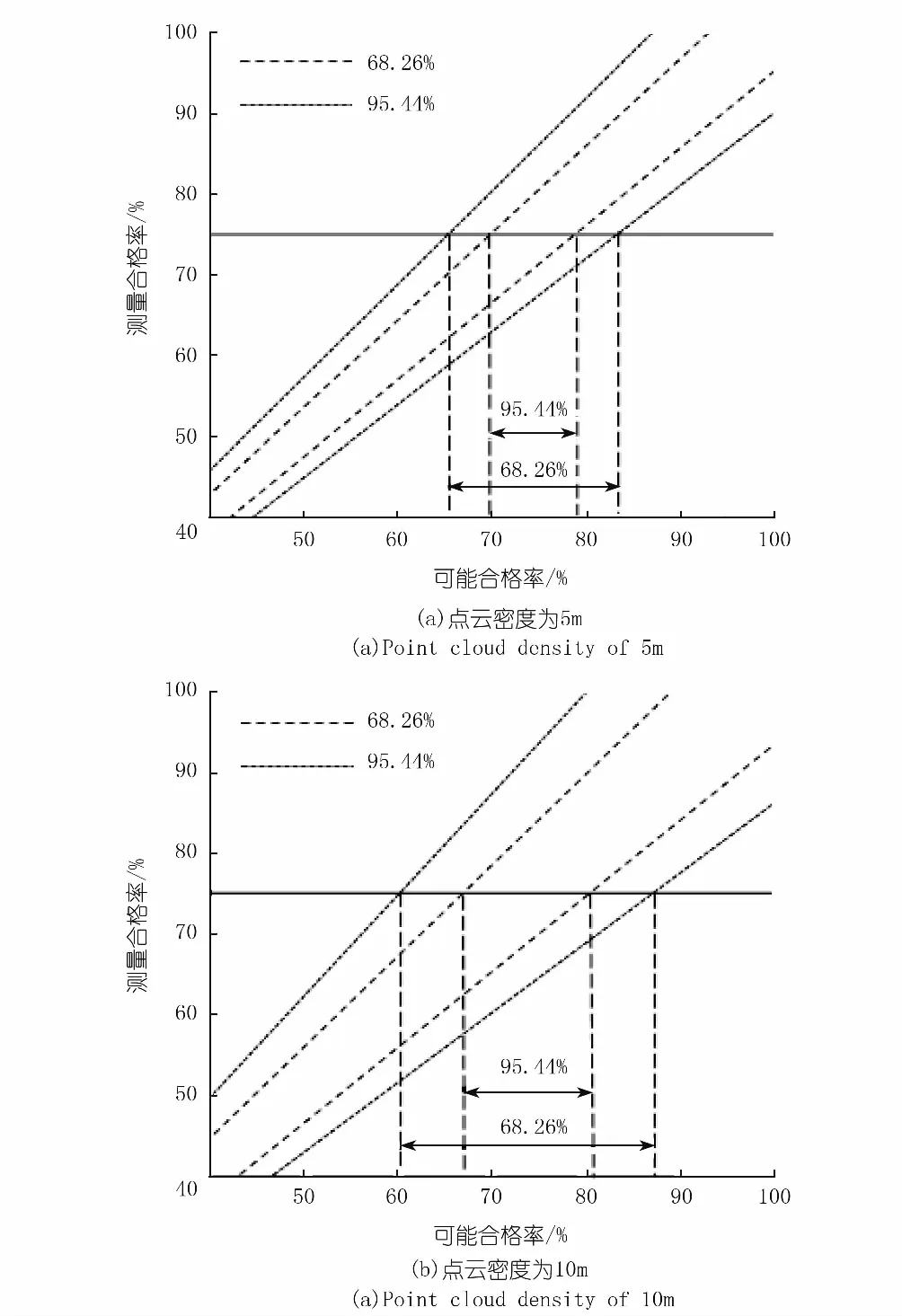
图6 不同置信概率下测点合格率可能分布范围Fig.6 The possible distribution range of qualified rate under different confidence probabilities

由图6可知：① 当置信概率相同时，点云密度为5 m时的相对误差范围始终小于点云密度为10 m时的相对误差范围；② 在相同置信概率下，随着测量合格率的增加，合格率可能分布的范围也逐渐增加；③ 点云密度为5 m时，当测量得到的合格率为75%时，在置信概率分别为95.44%和68.26%条件下，合格率真值的可能分布范围分别为65%～83%和70%～78%；点云密度为10m时，当测量得到的合格率为75%时，在置信概率分别为95.44%和68.26%条件下，合格率真值的可能分布范围分别为60%～87%和67%～80%，显然点云密度为5m时区间较窄，评价结果精度更高，结果的可靠性也较高；④ 在进行抛石效果分析时，如遇重要施工区，如河流水势急剧变化区域，应选择精度较高的点云数据(如5 m)，在河势较平稳区域及水下地形冲淤变化不明显的区域，可选择点云密度为10 m的数据进行抛石效果评价。

3 结 论

本文通过对选取区域的抛石增厚值作误差分析并引入测量不确定度理论进行研究，可得到如下结论。

(1) 点云密度对河势急剧变化区的抛石效果评价结果的影响较为显著，评价结果的误差随点云密度的增加呈先增加后逐渐稳定的变化趋势。

(2) 在置信概率相同的条件下，点云密度越低，其抛石效果评价结果的不确定性越小，相应的可靠程度越大。

研究不仅证明了评价结果的误差呈正态分布的普遍规律，还给出了不同点云密度下评价结果的不确定性，为河势急剧变化区水下抛石评价选取合适的点云密度提供了借鉴。