基于Matlab GUI的X型圈选配仿真平台开发*

魏 望,刘洪宇,余三成,欧阳小平,江文达

(1.浙江大学 机械工程学院·杭州·310027； 2.上海航天控制技术研究所·上海·201109)

0 引 言

伺服机构与火箭发动机构成了推力矢量控制系统,跟随箭载计算机的控制指令进行运动,对火箭的姿态进行控制。油箱蓄压器组件属于伺服机构主要的油源部件,负责为伺服机构提供增压油和瞬时峰值流量。目前,油箱、蓄压器所使用的X型密封圈是一种由4个O型截面组成的类似于字母“X”的密封圈。其在O型圈的基础上演变而来,具有良好的自润滑性、防扭转性能,且摩擦系数较低,可被广泛应用于往复密封的液压领域[1-4]。密封件在配对时,依赖技术人员的经验选择,耗费时间长,且无法使所有工件实现最优选配方案；在装配过程中,由于零件精度高,需要对装配轴向力进行严格控制,而轴向力的变化情况在装配前未知,这不利于对装配过程进行监控,以及对装配结果进行预测。

Matlab语言在复杂的数值分析、矩阵运算等方面具有显著的优势[5],可用来编写选配程序,提高计算速度,但Matlab程序无法脱离软件环境运行,使用不便且不易推广。黄乐等通过ANSYS软件对橡塑密封件进行了固体力学分析,获得了静态接触压力和接触区的影响系数矩阵[6]；Sussman等借助计算机仿真软件,获得了橡塑密封件在受压变形时的接触压力、形变等信息[7]；薛志全对O形密封、VL形密封的结构进行了有限元分析,获得了多工况下接触压力的分布[8]。但是,仿真软件的分析流程复杂,结果提取不便。Matlab GUI(图形用户界面)可整合两者的优点,充分利用Matlab的计算能力,并可调用有限元分析软件进行计算仿真,且开发的界面操作简单,结果显示直观。

本文通过Matlab GUI开发仿真平台,将选配仿真过程分为X型圈选配模块与装配模块两部分:选配模块根据输入的零件尺寸信息及预定策略进行综合配对,输出选配结果；装配模块得到选配模块提供的配对信息,并调用商业软件ANSYS实现密封件的应力应变分析。仿真平台在读取结果后,在程序界面内直观显示工件在装配过程中的轴向力变化曲线。

1 选配模块开发

选配对象为两型号的油箱蓄压器组件,包括油箱壳体、油箱活塞及与之相配合的X型密封圈,蓄压器壳体、蓄压器活塞及与之相配合的X型密封圈,其典型结构如图1所示。

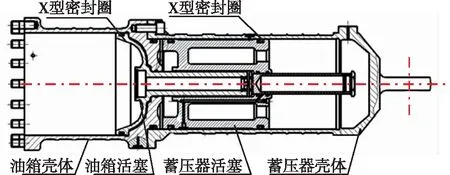
图1 油箱蓄压器组件Fig.1 Fuel tank accumulator assembly

选配模块整体流程:①尺寸输入界面读入零件尺寸信息；②将零件尺寸输入选配界面后,根据预定评分区间及间隙、压缩率、拉伸率权重参数进行密封副评分；③将密封副评分与密封副权重相乘后求和,得到综合评分；④以最优原则为选配原则,循环输出最大值组合。整体流程如图2所示。

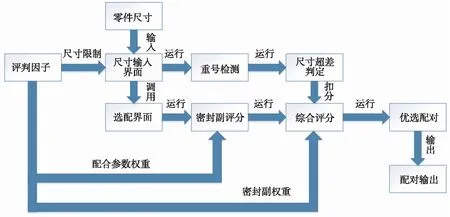
图2 选配模块流程图Fig.2 Flow chart of the matching module

为实现最优选配原则,设立了考虑3个匹配参数(间隙、压缩率、拉伸率)、同时考虑密封副重要性分配的综合量化评分体系。

其中,压缩率Y为

(1)

式(1)中,h为密封圈槽底至密封面的距离,b为密封圈的截面直径。

轴沟槽密封的拉伸率τ为

(2)

孔沟槽密封的拉伸率τ为

(3)

式(3)中,D1为槽的公称直径,Dd为轴的公称直径,D为密封圈的公称直径,d为密封圈的截面直径。

以某密封副压缩率评分为例,其具体算法如下

(4)

(5)

其中,ys为压缩率；m为压缩率区间；pmax、pmin为压缩率在区间m内的最大、最小评分值；pb为压缩率评分。当ys位于压缩率中值左侧时,适用公式(4)；当ys位于压缩率中值右侧时,适用公式(5)。压缩率取值范围为8%～16%。具体评分规则为,将该范围划分为4个评分区间,按照中值评分最高,左右区间依次递减顺序评分。其中,以12%(中值)为最高评分10分；10%～12%为中值左侧第一个区间,评分递减至9～10分取值,按照距离中值的距离线性降分；12%～14%为中值右侧第一个区间,评分递减至8～9分取值,按照距离中值的距离线性降分；8%～10%与14%～16%区间按照以上规则依次减分。

一组配对零件含有2个密封副(P1,P2),根据2个密封副的重要性赋予其权重值φ,故每组零件的总分为

P0=P1φ1+P2φ2

(6)

对每个密封副评分:将间隙(Pj)、压缩率(Py)与拉伸评价参数(Pl)的取值范围分为若干个等级并赋予其评分,并根据3个评价因子的重要性赋予其权重值φ,故每个密封副的得分为

P1=Pjφj+Pyφy+Plφl

(7)

以某油箱组合评分为例,具体算法如下

pj=(pa·a1+paa·a2+paaa·a3)·c1+

(pb·b1+pbb·b2+pbbb·b3)·c2

(8)

式(8)中,pj为一组配对零件的总分,pa、paa、paaa依次为密封副1中3个配合参数(压缩率、间隙、拉伸率)的评分；pb、pbb、pbbb依次为密封副2中3个配合参数(压缩率、间隙、拉伸率)的评分；a1、a2、a3依次为密封副1的压缩率、间隙、拉伸率的权重值；b1、b2、b3依次为密封副2的压缩率、间隙、拉伸率的权重值；c1、c2分别为密封副1与密封副2的权重值。具体评分规则为,先根据3个参数的得分与权重计算每个密封副的得分,每个密封副再与自身权重值相乘后求和,得到一组配对零件最终的评分。

此外,当遇到超差零件时,为了最大限度地利用零件及为了区分于公差内零件,需将超差零件的评分适当降低。基于以上考虑,将所有可能组合依次评分后,按分数高低优选出最佳组合。

基于Matlab强大的运算能力,所有零件任意配对的评分均可以立刻得到,但将庞大数据通过排序法取最大值的过程则耗时较长,故需要优化算法:从数据矩阵中找出最大评分,输出该组合数据,并得到组合内所有出现的零件、密封件编号；将数据矩阵内含有重复编号的组合评分归零,继续寻找最大评分组合,直至循环输出所有结果。经算法优化后,计算速度明显提升,可在数秒内获得结果。程序的流程图如图3所示。

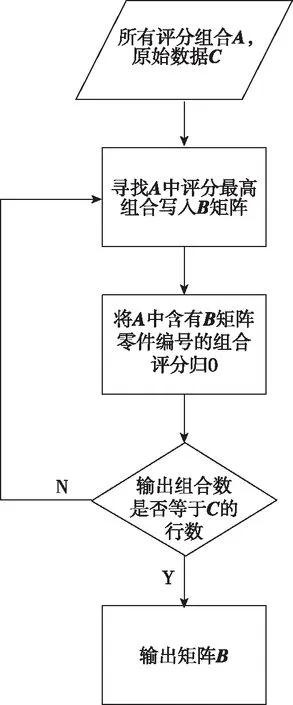
图3 输出最优选配结果的流程图Fig.3 Framework of the most preferred result output

其中,A、B、C变量分别存储所有评分组和、最优选配结果、原始数据。规定循环次数为原始数据C中的行数。此处,行数代表所有零件配对的最大可能组数；随后,使用Matlab矩阵运算max函数,并找出所有评分组合A中的最大组合。如果该组合评分大于0,则将其写入最优选配结果B矩阵。第二个for循环语句将最优选配结果B矩阵中已经选用的零件在A矩阵内对应的组合评分归0。在下一循环取最大值的过程中,这些组合将不会再被选中。最后,循环输出所有结果,并将结果保存在最优选配结果B中。

2 装配模块开发

模块功能:将零件尺寸信息、橡胶模型参数、摩擦系数导入仿真软件中进行运算。在仿真软件中建模求解油箱、蓄压器装配过程中的接触压力变化,提取数据并转化为轴向力的变化曲线。

装配模块流程为:①装配模块读取选配模块配对结果,将零件尺寸信息、仿真材料参数、摩擦系数通过Matlab写入程序输入文件,以备ANSYS调用；②装配模块通过Matlab函数调用ANSYS程序,并读取指定ANSYS仿真命令流文件；③ANSYS程序根据程序输入文件,建立密封件模型并求解密封件的接触压力,输出接触压力数值与图像；④装配模块将调用的接触压力数值经过计算转换为轴向力数据并进行显示,调用接触压力图像并进行显示。选配模块的流程图如图4所示。

图4 装配模块的流程图Fig.4 Flow chart of the assembly module

2.1 有限元分析计算

(1)几何模型

油箱组件典型密封副的结构示意图如图5所示。由于密封圈是轴对称的,且其安装在油箱壳体和油箱活塞的往复运动密封副处的边界受力条件也具有轴对称性。因此,其可被简化为平面轴对称模型并进行有限元分析。

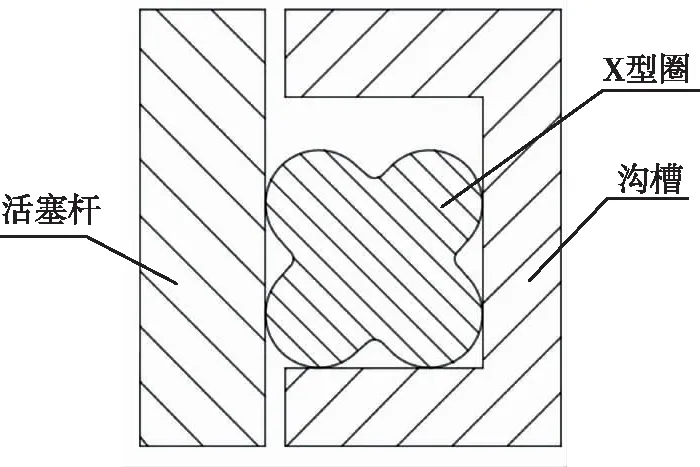
图5 油箱组件典型密封副Fig.5 Typical seal pair of the fuel tank assembly

(2)材料模型

密封圈材料为橡胶材料,橡胶材料属于超弹性材料,具有材料非线性特性。针对橡胶的非线性特征描述,现在比较常用的是唯象法,即根据其可观的表象物理性质去推断其模型。在多数情况下,将橡胶的不可压缩性作为研究载体,以不能对其做功为基础,推导其能量关系。很多学者给出了自己的方法,其中有3种描述方法的应用最为广泛,即Mooney-Rivlin[9-10]、Ogden[11-12]和Neo-Hookean[13]3人提出的数学物理模型。

ANSYS、NASTRAN、ADINA、MARC等大型通用非线性有限元程序一般采用Mooney-Rivlin模型进行分析和计算橡胶材料的力学性能[14]。本文选择Mooney-Rivlin模型来定义橡胶的材料特性。橡胶材料的单元公式需考虑不可压缩条件,所以分析单元类型可考虑选择PLANE183[15]。该单元具有二次位移函数,能够很好地适应不规则模型的分网,可用作平面单元或轴对称单元。

(3)载荷步设置

X型圈的初始位置为其自然伸长状态,定义第1个载荷步使套筒移动到标准沟槽位置,使X型圈处于安装压缩状态；定义第2个载荷步使活塞杆从密封区域外逐渐向X型圈水平移动,使之与X型圈接触,并逐渐将X型圈压紧在密封槽内。

(4)驱动元件的引入与轴向力的获取

为了仿真实际装配过程中活塞杆所受的轴向力,可计算密封圈与活塞杆的水平作用力与摩擦力之和,但计算流程较为繁琐。本文采取的方式为在活塞杆后侧加入一个驱动元件(方形结构),推动活塞杆运动,得到驱动元件与活塞杆的接触压力,进而计算其与活塞杆之间的相互作用力,等效得到轴向力。

利用时域后处理,将驱动元件接触压力与对应时间写入预先定义数组内,并通过ANSYS输出。装配模块读取文件后,将时间转化为位移量,将接触压力与接触面积相乘并转换为轴向力(其中,零件尺寸信息已内置于程序),并在装配界面内作出轴向力随活塞杆位移变化的图像。

2.2 结果分析

(1)以油箱组件某密封副为例分析装配过程中轴向力的变化趋势。模型尺寸如图6所示。在装配过程仿真中,套筒固定,活塞杆向X圈移动,摩擦系数为0.01。

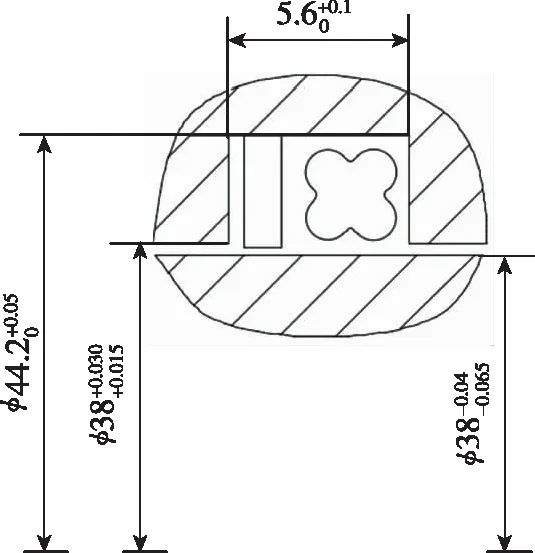
图6 油箱组件某密封副尺寸Fig.6 The seal pair parameters of the fuel tank assembly

图7展示了活塞杆在运动过程中,轴向力随位移变化的仿真结果。轴向力的图像为双峰曲线,峰值发生在挤压X型圈的两个末端并产生较大变形的位置。在第一波峰(图8a),轴向力主要由接触压力Y向分量组成；在第二波峰(图8b),轴向力主要由接触压力Y向分量与摩擦力共同组成。在最后的稳定状态下,轴向力较小。

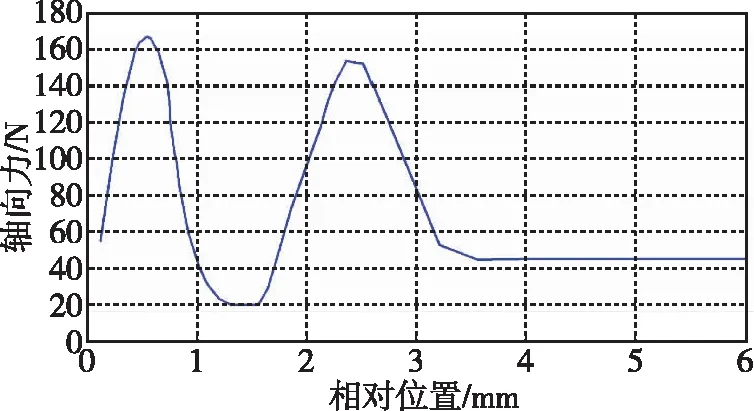
图7 装配过程中的轴向力曲线Fig.7 Axial force during assembling

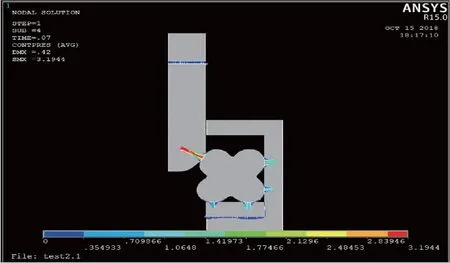
(a)轴向力第一波峰时的接触压力图像

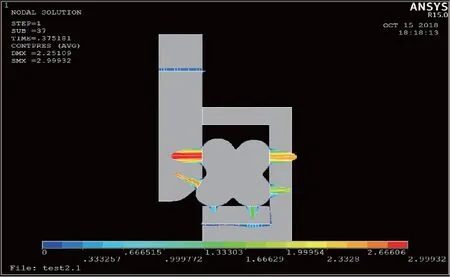
(b)轴向力第二波峰时的接触压力图像图8 轴向力波峰时的接触压力图像Fig.8 Contact pressure when axial force peak

(2)以蓄压器组件某密封副为例,仿真分析摩擦系数、压缩率与轴向力的关系。模型尺寸如图9所示。在装配仿真过程中,套筒固定,活塞杆向X圈移动。

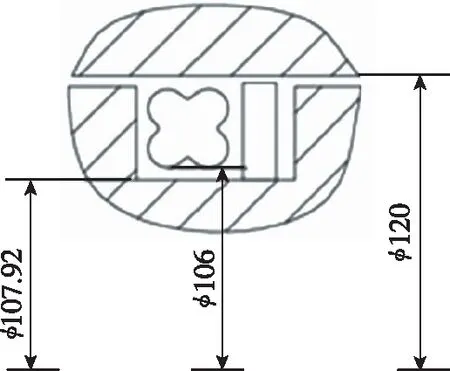
图9 蓄压器组件某密封副的尺寸Fig.9 The seal pair parameters of the accumulator assembly

图10展示了在不同摩擦系数下轴向力的仿真结果。随着摩擦系数的增加,轴向力峰值增加,分别为420N(摩擦系数为0.05)、569N(摩擦系数为0.1)、624N(摩擦系数为0.15)。趋势为逐渐增大,而最大轴向力出现的位置几乎不变。最终,稳定轴向力逐步增大,分别为72N(摩擦系数为0.05)、177N(摩擦系数为0.1)、244N(摩擦系数为0.15)。

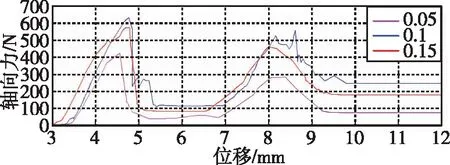
图10 不同摩擦系数下的轴向力曲线Fig.10 Axial force under different friction coefficients

图11展示了不同压缩率下轴向力的仿真结果。随着压缩率的增加,轴向力峰值增加,分别为289N(压缩率为9.17%)、569N(压缩率为11.18%)、627N(压缩率为13.09%)。趋势为逐渐增大,但增幅变小,最大轴向力出现的位置发生了变化。最终,稳定轴向力逐步增加,但增幅变小,分别为113N(压缩率为9.17%)、177N(压缩率为11.18%)、190N(压缩率为13.09%)。

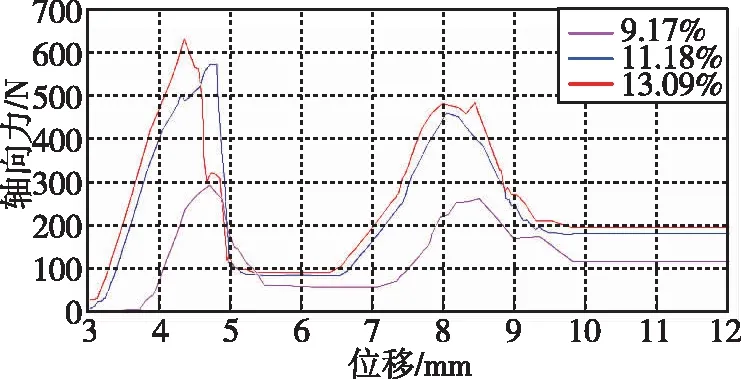
图11 不同压缩率下的轴向力曲线Fig.11 Axial force at different compression ratios

3 软件界面

3.1 选配模块

尺寸输入界面主要完成信息读入与显示:在操作时,只需点击读取文件按钮,选取文件位置,程序将自动读入信息并将信息显示在表格内。尺寸输入界面如图12所示。

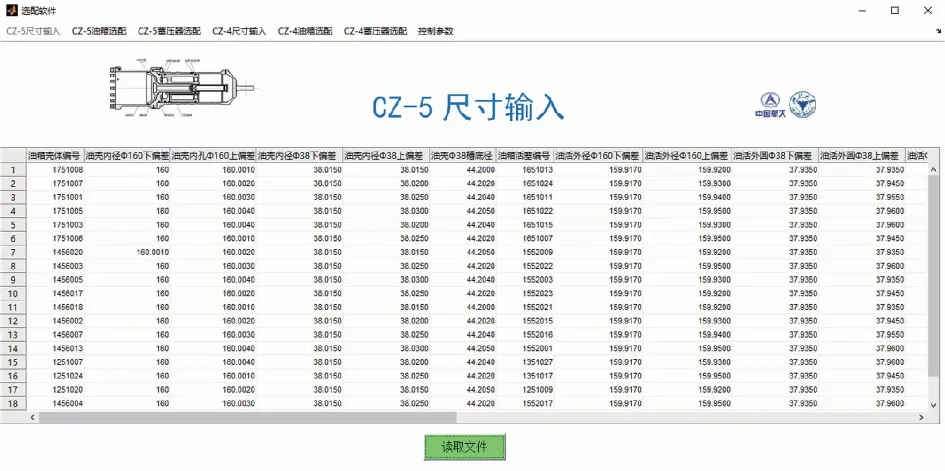
图12 零件尺寸输入界面Fig.12 The input interface of component size

选配界面将零件的尺寸信息与控制参数相结合,进行零件的密封副评分、综合评分、优选配对,并输出格式为“.xls”的结果文件。在尺寸信息读取完成后即可点击配对按钮,程序将自动计算最优选配结果,并将结果显示在界面表格内。结果信息包含零件编号、尺寸信息、评估参数、综合评分。单击结果输出,选择保存文件位置,即可输出文件。选配界面如图13所示。

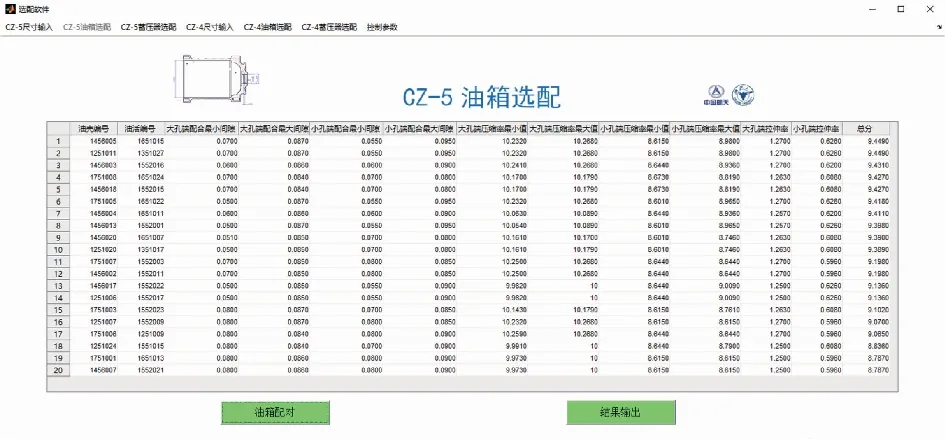
图13 油箱组件的选配界面Fig.13 The matching interface of the fuel tank component

3.2 装配模块

装配模块界面如图14所示。界面左侧分为基础信息与参数输入两部分。零件配对信息可通过数据导入按钮显示在基础信息栏内,信息包含零件编号、间隙尺寸、压缩率等；参数输入包含橡胶材料Mooney-Rivlin模型的参数和摩擦系数。

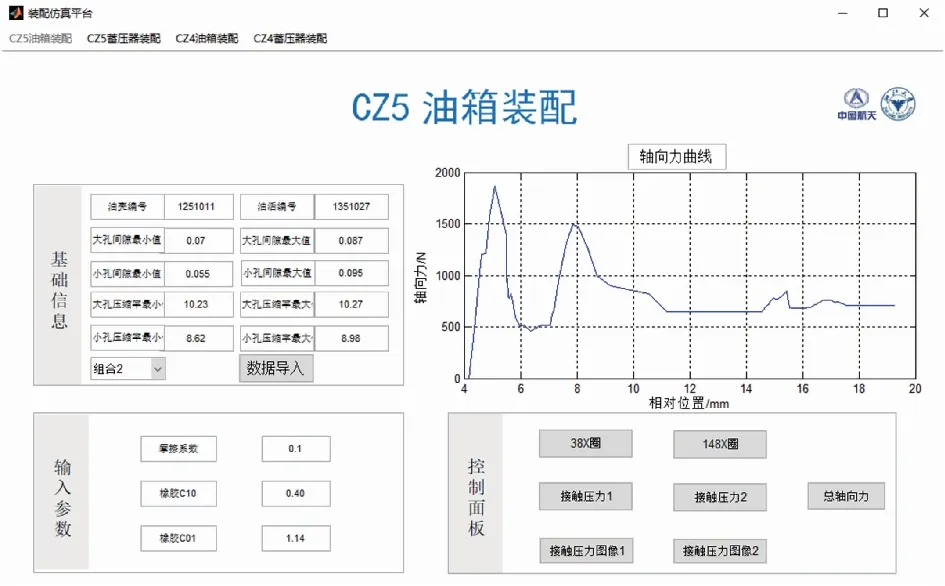
图14 油箱组件的装配界面Fig.14 The assembly interface of the fuel tank component

右侧分为轴向力曲线与控制面板两部分。控制面板的第一行按钮用来调用仿真,其回调函数可通过system函数调用ANSYS软件进行仿真。第二行按钮用来在仿真结束后导入结果,并将结果自动换算为轴向力显示在坐标轴中。第三行按钮用来在仿真结束后显示图像结果,该图像结果为仿真终止位置时的接触压力图像。该图像可用来判断仿真是否计算正确,并取得了完整结果。

4 结 论

(1)本文提出了一种考虑3个匹配参数(间隙、压缩率、拉伸率)、同时考虑密封副重要性分配的综合量化评分体系,实现了对配对零件密封性能的综合评分。

(2)通过引入驱动元件,直接获得了轴向力变化曲线。在装配过程中,轴向力主要受摩擦力与轴向接触压力的影响,其变化趋势为双峰曲线；当摩擦系数增加时,轴向力峰值、最终稳定轴向力将增加；当压缩率增加时,接触压力相应增加,轴向力峰值、最终稳定轴向力将增加,但增幅变小。