针对不平衡数据的PSO-DEC-IFSVM分类算法

魏建安 黄海松 康佩栋

（贵州大学现代制造技术教育部重点实验室，贵阳，550025）

引 言

随着大数据时代的到来，信息量激增，由此产生大量的不平衡数据集，即数据集中某类样本数远小于其他类的样本数，其中样本数较少的类叫做正类，样本数较多的类称为负类。不平衡数据的分类作为数据挖掘与机器学习的重要研究内容，近年来越来越多的国内外学者对其进行了大量的研究[1-3],并将其广泛应用于故障诊断、医疗诊断及信用卡欺诈[4-8]等领域。

在众多机器学习算法中，支持向量机（Support vector machine,SVM）算法是依据统计学习中VC维理论以及结构风险最小化等原则而提出的一种学习方法，能够有效地处理小样本、非线性与高维度等问题，且作为一种有效的分类算法，已经获得广泛的应用。但传统SVM对原始数据的处理是基于样本集是平衡的，即正负类样本的数目相同。显然，对于不平衡数据传统SVM算法的分类效果并不理想，这是因为当数据集不平衡时实际分类超平面会向少数类方向偏移，从而导致少数类样本的识别率变低。目前，对于传统SVM算法可以从以下两个方面进行改进以获得更加理想的分类效果：（1）重构原始数据集，即通过过（欠）采样方式分别对正负类样本集进行重构，常见的方式有：对于过采样有基于SMOTE（Synthetic minority oversampling technique）的过采样方式及其改进算法等[9-10],对于欠采样方式有随机欠采样以及基于样本特性的欠采样等[11-12]。但是实际上以上方法是通过一定的准则通过增加或者减少原始数据集的样本数来调节数据集本身的不平衡性，具有随机性较大、盲目性较高、稳定性较差等缺点，且当数据集严重失衡时，所利用的采样方法可能效果不佳。（2)改进的SVM算法，即针对正负类样本数目上的差异，通对算法本身的改进，以增强算法本身对不平衡数据的适应性。常见的改进算法有：不同惩罚因子(Different error costs,DEC)算法及其改进算法通过正负类样本赋予不同的惩罚因子以提高分类的准确性[13-14]；模糊支持向量机（Fuzzy support vector machine,FSVM)及其改进算法通过将模糊数学和支持向量机相结合以克服噪声或野点对支持向量的影响来提高分类的准确性[15-17]；此外，还有在赋予不同的惩罚因子的同时，增加新的约束条件的近支持向量机法等[18]。

因模糊支持向量机在处理不平衡数据时有较好的表现，故本文选取FSVM进行不平衡数据的分类。现阶段比较典型的模糊支持向量机的改进方式有：李苗苗等[19]在设计模糊隶属度函数时考虑了每个样本点到类型中心距离的同时还考虑到了该样本点最邻近的K个其他样本点的距离。Batuwita等[20]将模糊支持向量机与DEC算法进行结合提出一种FSVM-CIL算法，用于处理不平衡数据以及噪声样本，该算法在设计模糊隶属函数时与传统FSVM类似，仅考虑样本到类中心的距离；鞠哲等[21]在设计FSVM的模糊隶属度函数时考虑样本到类中心距离的同时还考虑到了样本周围的紧密度，并将FSVM与DEC有机地结合，即DEC-FSVM-Ju算法。但是鞠哲等的算法存在以下缺点：（1）算法复杂程度增加，同时未对增加的参数合理优化；（2）没有考虑到样本特性的影响；（3）优化效果不明显。针对上述算法的缺点，本文在设计模糊隶属度函数时考虑样本到类中心距离以及样本周围紧密度的同时，还考虑到了样本信息量特性的影响并赋予不同样本不同的权值，此外将改进的FSVM算法（Improved fuzzy support vector machine,IFSVM）与DEC算法进行结合，并应用粒子群算法（Particle swarm optimization,PSO）对该改进算法引入的参数进行寻优，得到PSO-DEC-IFSVM算法。最后将PSO-DEC-IFSVM算法应用于UCI机器学习数据库中的6类不同的不平衡数据集中。实验证明：本文所提算法相对于已有算法在处理含有噪声的不平衡数据集分类时具有更好的分类效果。本文结果为不平衡数据的分类提供了一个有效的理论模型。

1 算法简介

1.1 传统SVM算法

以传统二分类为例，SVM的基本原理为：从样本（或者核）空间内寻求一个最优分类超平面，使得正负类样本分隔间距达到最大化。假定给定训练集为(X,Y)={(xi,yi)},yi∈{-1,1},i∈1,2,3,…,n，其中：xi,yi分别为训练集的第i个样本以及样本的标签。在SVM算法中引入核函数（K）将训练集引入高维空间，即K(x,y)=φ(x)Tφ(y)，其中φ(x)为非线性映射；同时引入松弛变量ξi≥0,i=1,2,3,…,n与惩罚因子C，综上,给出标准的支持向机一般形式为

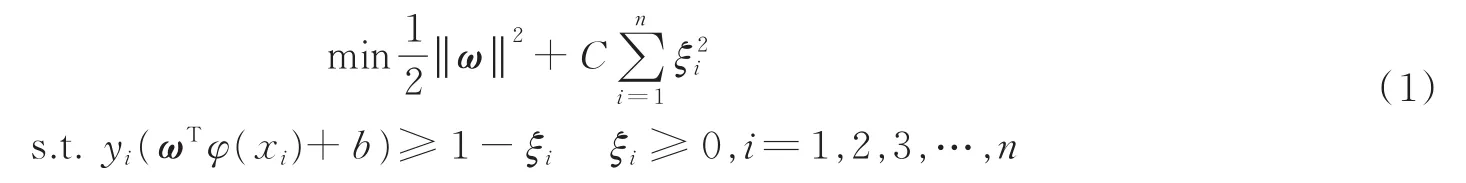
对于式（1）的优化求解，可引入Largrandge乘子法转化为对偶形式，即

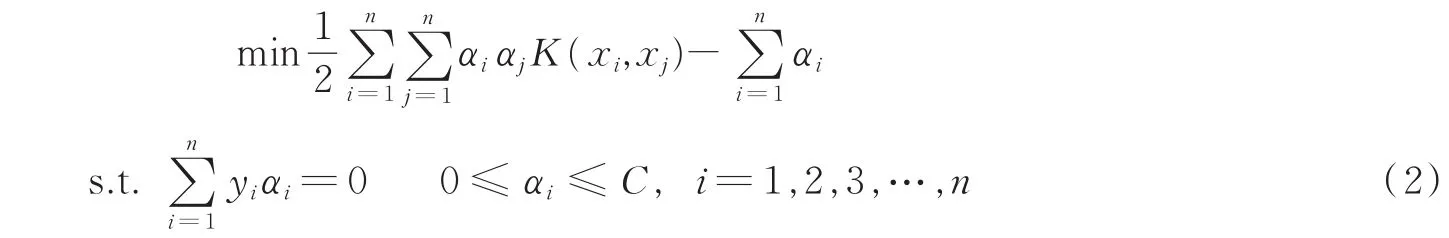
假定对偶问题的最优解为α*，则可反求出数据集最优分类超平面的法向量ω*与截距b*，其解法如式（3，4）所示，最终利用传统SVM方法构造出如式（5）所示的决策函数。

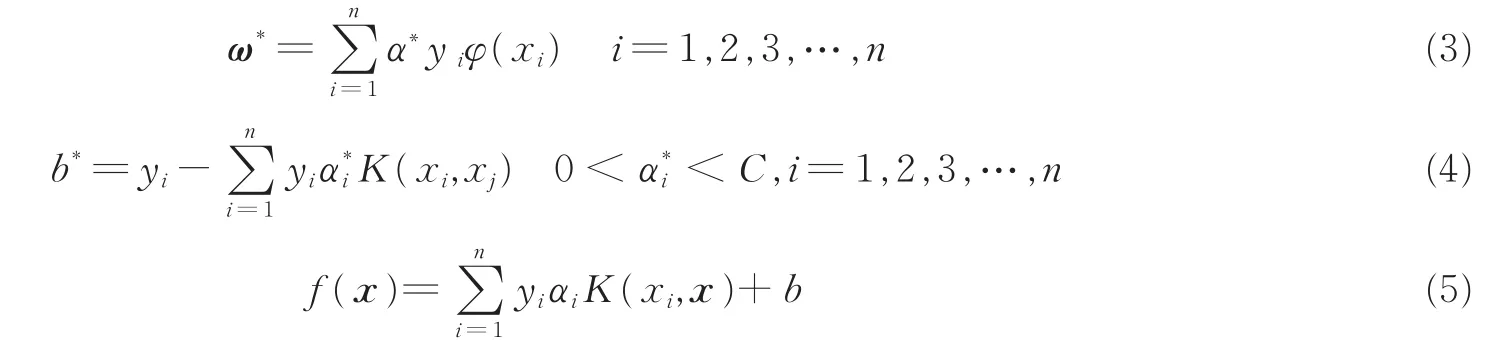
1.2 FSVM算法与DEC算法的结合算法

事实上，实际生产生活中的数据集往往是不平衡的，相比传统SVM算法分配给每一个样本相同的权值，FSVM算法和DEC算法相结合的DEC-FSVM算法根据样本的不平衡性以及重要性分配不同的权值，以提高分类的准确率。同上，对于二分类而言，假定给定训练集为(X,Y)={(xi,yi)},yi∈{-1,1},i∈1,2,3,…,n，另假定原始数据集中有m个样本为正类样本(即yi=1,i=1,2,3,…,m)，则剩余的n-m个样本为负类样本(即yi=-1,i=m+1,m+2,m+3,…,n)，则用于不平衡数据分类的模糊支持向量机的一般形式如式（6）所示。

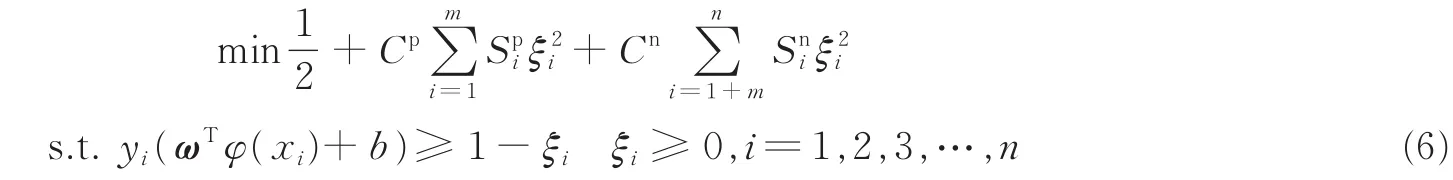
式中：Cp，Cn分别代表正负类样本的惩罚因子，以表示两类间的不平衡性；，分别代表正负类样本的隶属度函数，以反映该样本在其所属类别中的重要性。从式（6）可以看出相对于传统SVM算法，DEC-FSVM从惩罚因子与隶属度函数的引入方向作了改进，这将更有利于不平衡数据的分类。

2 改进的模糊支持向量机（IFSVM）工作机理

2.1 模糊隶属度函数的设计

Lin等[15]提出将样本到其类中心的距离作为衡量样本重要性的指标。即将模糊隶属度函数定义为

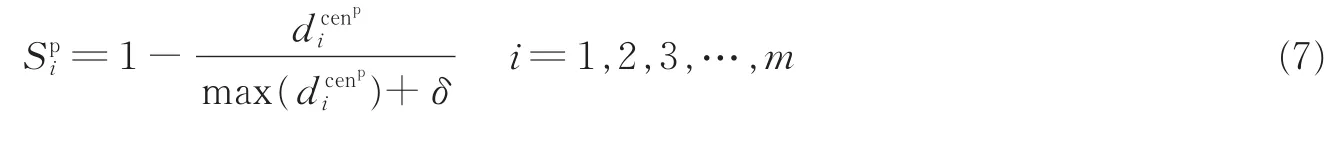
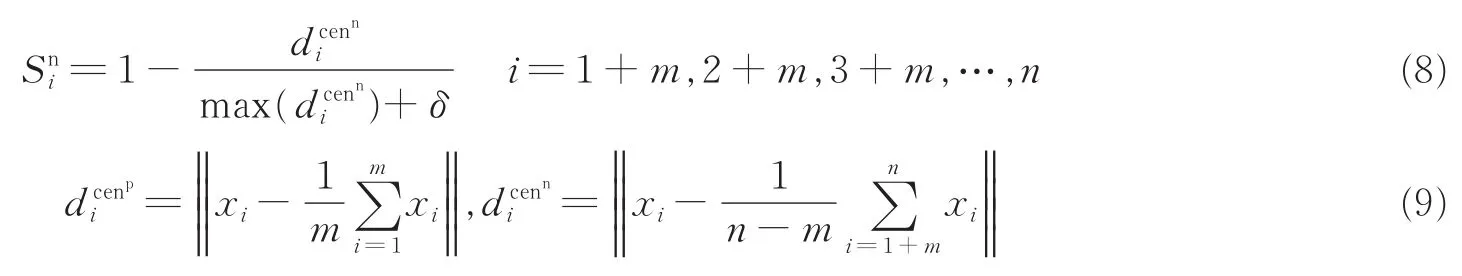
式中：,分别代表正负类的第i个样本到其类中心的距离；δ为引入的一个非常小的正数，用来保证隶属度为正。但是当数据集分布不规则时，运用该方式很可能将噪声或野点作为正常的正负类样本进行训练，最终导致算法的整体分类精度降低。如图1（a）数据集1所示，假设P1为一噪声点，对于正常样本集（以负类为例）来说仅考虑样本到类中心的距离时P1将被当做正常点进行训练赋予正常隶属度函数值，显然是不合理的。

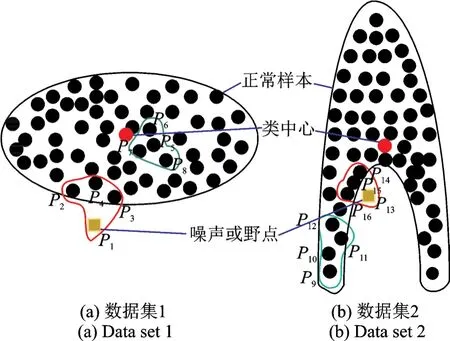
图1 不同数据集下噪声点与正常样本的位置关系Fig.1 Relationship between the noise points and the normal samples under different data sets

针对上述问题，文献[21]中提出在设计模糊隶属度函数时需综合考虑样本到类中心的间距及其周围的紧密度，且其紧密度的衡量方式应用K-近邻域准则，即如图1（a）所示：在图中拟取K=3，对于负类样本来说对于噪声点P1的距离最近的3-近邻域点集为{P2，P3，P4}，负类样本的任一正常样本P5的距离最近的 3-近邻域点集为{P6，P7，P8}。显然，负类的正常样本点P5的3-近邻域点集的距离均值大于噪声点P1的3-近邻域点集的距离均值，故文献[21]引入式（10，11）定义样本周围的紧密度为

式中：(xi)为正（负）类的第i个样本的K-近邻域的集合，显然如果某样本的值越小则该样本属于该正（负）类可能性越大。反之如果该样本为噪声或者野点的值将会较大，故将模糊隶属度函数定义如下

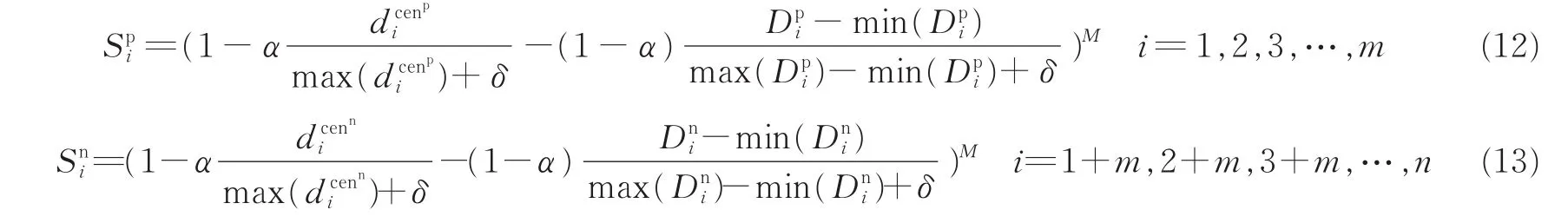
式中：α为一个权值，用于均衡样本到类中心与样本的近邻域密度重要性，故对于不同数据集，α（α∈{0,0.1,0.2,…,1}）值合理的选取极为重要；δ的意义同上；M（M∈{0.1,0.2,0.3,…,1}）用于调整所有样本模糊隶属度函数的范围，故值的选取亦较为重要；此外，对于样本K-近邻域中的K值，为了简单起见，文献[21]在隶属度函数设计时将所有样本取为同一值，但是由图1（a,b）可以看出，对于1，2两种不同的数据集，如果K值同时取为一定值是不合理的，对于数据集1来说K取为3是合理的，但对于数据集2，假设P13为一噪声点，对于负类样本来说距离噪声点P13最近的3-近邻域点集为{P14，P15，P16}，距离负类样本的一正常样本P9最近的3-近邻域点集为{P10，P11，P12}。显然，负类的正常样本点P5的3-近邻域点集的距离均值小于噪声点P13的3-近邻域点集的距离均值，在这种情况下，噪声样本P13会被当作正常的负类样本进行处理，这将会在较大程度上影响分类精度。

综上，对于以上所提的α，M，K等参数在利用DEC-IFSVM进行分类时均要进行优化，参数优化将于2.4节进行介绍。

2.2 FSVM算法的改进

当样本分布不规则时，前文提到文献[21]对FSVM算法改进时仅考虑到引入样本的紧密度来设计模糊隶属度函数，而没有考到样本本身的特性。众所周知：在运用传统SVM分类器进行分类时，分类超平面的确定只与支持向量有关，且SVM算法是通过分类间隙的最大化来设计分类超平面，以期获取较好的推广能力。同时文献[12]中提到：样本的信息量，即样本点到决策面的距离是判断该点性质的主要因素，且距离越近对分类超平面的影响越大。故本文在设计模糊隶属度函数时需要对信息量大的样本点赋予较大的隶属度函数值。据此，本文引入如式（14）所示的样本信息量的评价方式。

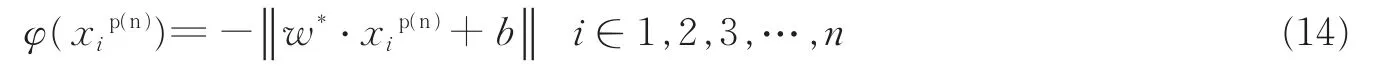
式中φ(xi

p(n))为第i个正（负）类样本信息量。图2为某数据不平衡下的理想超平面与实际超平面的位置示意图。从图2可以看出：对于理想分类超平面，正负类样本中的支持向量都是距离超平面很近的的点，故拥有最大的信息量；而对于偏移过后的分类超平面，正类样本的支持向量为距离分类超平面较远的样本点，负类的支持向量不变仍然为距离超平面较近的点。故运用传统支持向量机进行分类时，由于分类超平面发生严重偏移，正类样本φ(xip)信息量越小，相应的样本信息量越大；反之负类样本φ(xin)信息量越大时相应的样本信息量越大。另ω*与b分别代表传统SVM的分类平类超平面的法向量与阈值，故改进后的FSVM的隶属度函数如式（15，16）所示。

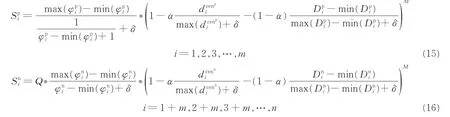
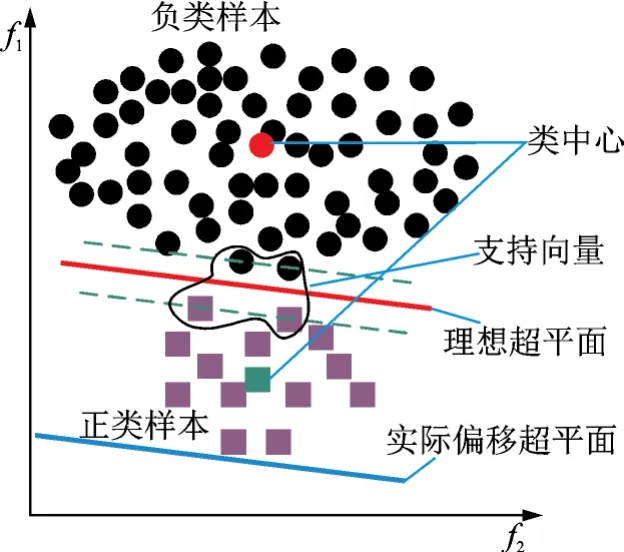
图2 数据不平衡下的理想超平面与实际超平面的位置Fig.2 Ideal hyperplane and the position of actual hyperplane under data imbanlance

式（15）中：φip为第i个正类样本的信息量，乘号（*）右边部分考虑了样本到类中心的距离及样本紧密度两个因素，而乘号（*）左边为正类样本信息量影响的表达式。上文提到运用传统支持向量机进行不平衡数据分类时，由于分类超平面发生严重偏移，正类样本φ(xip)信息量的值越小相应的样本信息量越大，故引入式（15）用于满足此规律，最终Sip即为正类样本基于改进的模糊支持向量机的隶属度。同样地，在式（16）中：φin为第i个负类样本的信息量，乘号（*）右边部分亦考虑了样本到类中心的距离及样本紧密度两个因素，乘号（*）左边为负类样本信息量影响的表达式。同样上文提到运用传统支持向量机进行不平衡数据分类时，由于分类超平面发生严重偏移，负类样本φ(xip)信息量的值越大时相应的样本信息量越大，故引入式（16）用于满足此规律，最终Sin即为负类样本基于改进的模糊支持向量机的隶属度。

另外，由于利用式（15，16）求正负类样本隶属度时，两式信息量影响的表达式不同，所以需引入平衡因子Q来保证正负类隶属度值范围一致。其算法为：正类所有训练样本的信息量影响值的均值除以负类所有训练样本的信息量影响值的均值所得到，表达式为

2.3 DEC-IFSVM惩罚因子的设置

众所周知，DEC算法通过赋予正负类样本不同的惩罚因子来提高SVM算法对不平衡数据适应性，对于正类样本赋予较大的惩罚因子，而负类样本赋予较小的惩罚因子。故本文提出DEC协同IFSVM优化算法，既有模糊支持向量机处理噪声（野点）的优势，又可以容易应对不平衡数据。基于样本特性的IFSVM的基本原理与算法上文已作阐述，对于惩罚因子的确定，文献[21-22]采取正负类样本比值的设定方式，且有较好分类效果，故本文亦采取此方式，即正负类的惩罚因子的算法为：Cp=C(nm)/m，Cn=C,其中：Cp为正类的惩罚因子；Cn为负类的惩罚因子；n为训练样本总数；m为训练样本中正类样本的个数；C为惩罚因子的初始参数且C＞0。

综上，改进的DEC-IFSVM算法的对偶形式为

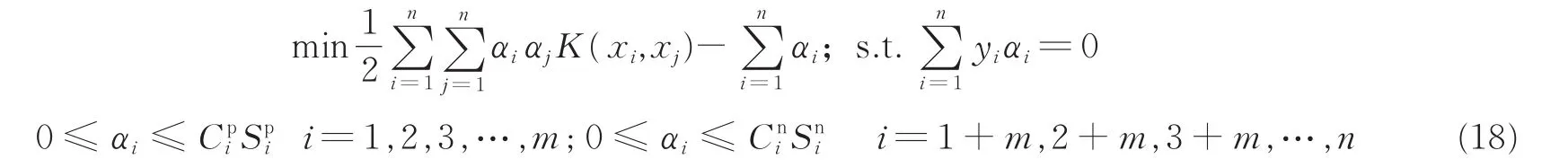
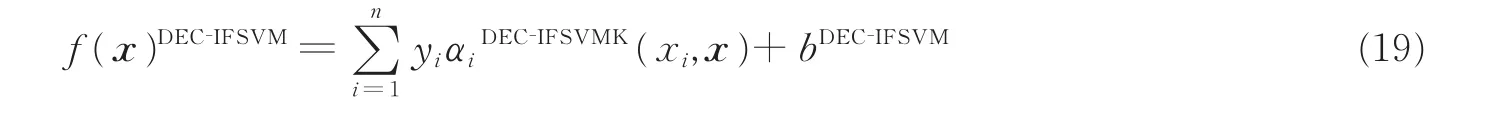
2.4 基于PSO算法的DEC-IFSVM参数优化

综合分析上文可知，运用DEC-IFSVM算法进行不平衡数据分类时，在算法复杂度增加的同时，为了得到更加良好的分类效果，需要对引入的α，δ，M，C，K等参数进行优化以及初值赋予。此外本文采用径向基（Radial basis function，RBF）核函数，故核函数中的参数g亦需要进行优化。

在上述需要进行优化的参数中：δ的初值赋予需要多次实验进行择优选取，而K，α，M，C，g五个参数拟利用PSO算法进行优化。

2.4.1 PSO算法简介

PSO算法是受鸟类捕食时搜索附近食物区域行为的启发,将问题的潜在解用不同的粒子来表示，寻找合适的适应度函数来确定各粒子的适应度。另外，PSO算法是一种并行的随机搜索算法，可以实现对解空间的搜索，同时，PSO算法具有控制参数最少、算法简单等优点，一经提出便得到广泛应用[7]。

2.4.2 参数优化

本文以不平衡数据分类效果的评价机制作为目标函数，K，α，M，C，g作为待求粒子，本文实验中采取十折交叉验证，对每一折的参数均进行优化。假定待求解的种群大小为N，迭代代数为G，Pi(i∈ 1,2,3,…,N)表示种群中i个体的位置，Vi(i∈ 1,2,3,…,N)与 fitnessi(i∈ 1,2,3,…,N)分别最终的则决策函数为代表i个体的速度与适应度值，故本文所采用的粒子群算法的求解步骤如下：(1)算法开始；(2)种群的初始化：包括粒子的位置Pi与速度Vi的随机初始化；(3)个体适应度值：根据目标函数来计算粒子的适应度值fitnessi；(4)循环迭代：在循环迭代过程中，寻找个体的极值Pbest以及整个群的极值Gbest；(5)算法终止：在满足最优解的条件下，终止循环。

2.4.3 优化结果

由上文可知，DEC-IFSVM引入的参数值需要进行优化，本文选取UCI数据集中的Pima等6种数据集，每个数据集进行十折交叉验证，由于每一折正负类样本数目不同，故需要对每一折的参数进行优化。最终，经粒子群算法优化后的K，α，M，C，g五个参数在不同数据集的最优参数如表1所示。

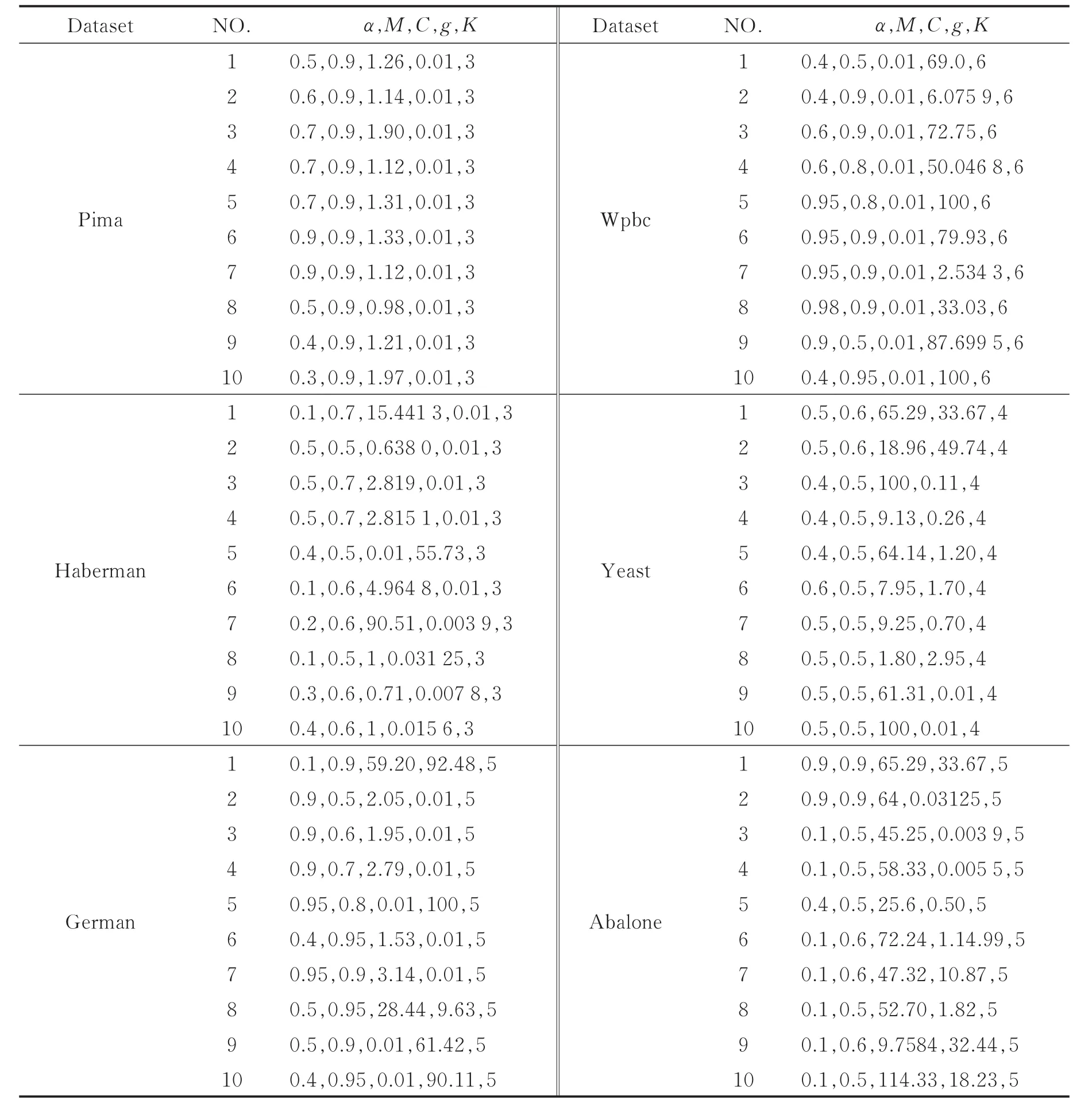
表1 PSO优化后DEC-IFSVM的最优参数Tab.1 Optimized parameters of DEC-IFSVM after PSO optimization

3 实验与结果分析

3.1 不平衡数据分类评价机制的引入

在数据集平衡的条件下，一般用数据集分类的总准确率对其分类效果进行评判，即：分类的总准确率越高，则分类器的分类效果越好；但是当数据集不平衡时，特别是不平衡比较大时，存在即使正类样本具有很低的辨识率的情况下，整体的分类准确率很高的情况，故该方式对于不平衡数据的分类准确率的评判是不准确的。为了克服单一分类准确率评价方式不令人信服的弊端，一些学者又提出了一些更加合理的评价机制：灵敏度（Sensitivity,SEN），即正类样本的分类准确率的评价机制；特异性（Specificity,SPE），即负类样本的分类准确率的评价机制；几何平均值（G-mean）,即分类器的综合评价机制。各评价机制的算法表达式为

式中：TP(++)为分类正确的正类样本的数目；FN(+-)为分类错误的正类样本的数目；FP(-+)为分类错误的负类样本的数目，TN(--)为分类正确的负类样本的数目，构成的混淆矩阵如表2所示。

分析上述3种评价机制可知：SEN的值越大正类样本的辨识率就越高；同样SPE的值越大负类样本的辨识率就越高；当SEN与SPE都较大时G-mean值就越大，反之G-mean值就越小。故对于不平衡数据选取G-mean值进行分类器的评价更加合理。

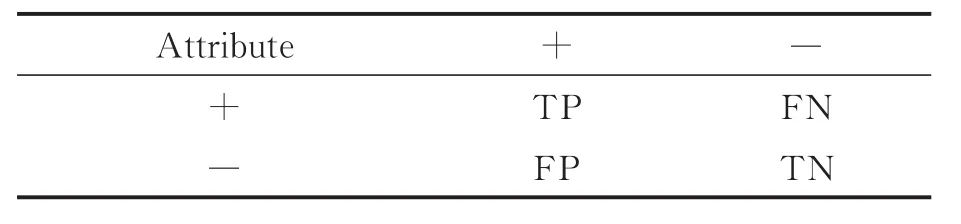
表2 混淆矩阵Tab.2 Confusion matrix

3.2 实验数据以及实验环境

为了突出本文所提算法在不平衡数据下分类的优越性，将所提算法（PSO-DEC-IFSVM）与现有算法进行对比，即：支持向量机（SVM）算法、模糊支持向量机（FSVM）算法、DEC算法、DEC结合FSVM的算法（DEC-FSVM）、DEC-FSVM-Ju算法以及利用PSO算法参数寻优前的DEC-IFSVM算法。同时，为了使实验结果更加具有说服力，本文在UCI机器学习数据中选取6种不同空间结构以及不同维度的不平衡数据进行实验验证，且这些不平衡数据必定会含一些噪声或野点个体。此外，为了减少训练的时间，每种不平衡数据集均随机选择部分作为实验，选取的6种不平衡数据集的基本特征如表3所示。

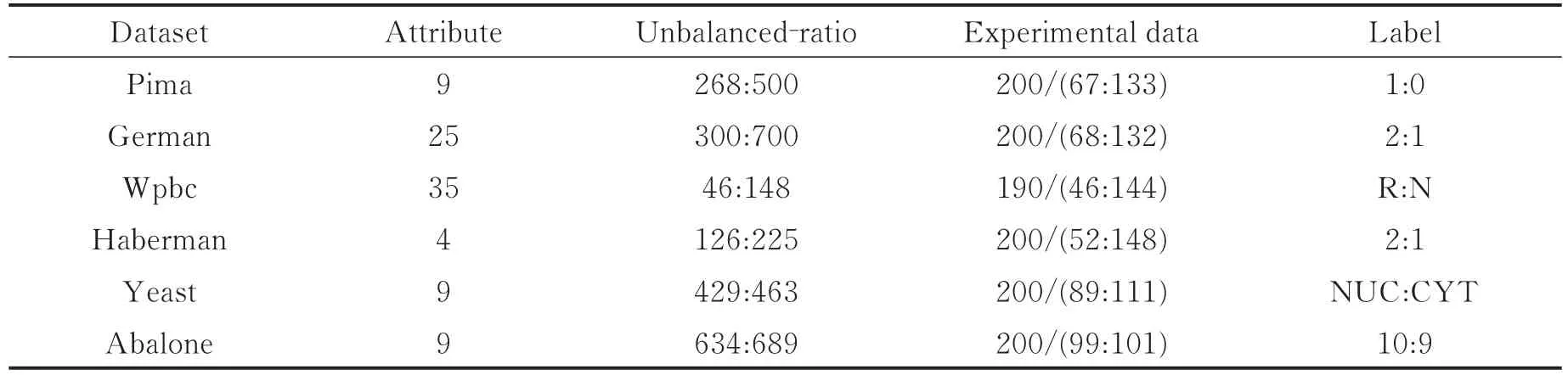
表3 实验中的6种不平衡数据集的特征Tab.3 Characteristics of the six unbalanced data sets in the experiment

本文所涉及的所有算法均采取十折交叉验证，且为了减少随机影响，每折运行十次，即对于一个不平衡数据将产生100组数据，最终将所得的100组数据的均值作为每种评价机制的最终值。本文所有算法的初始参数均为：δ=10-13，α=0.5，m=0.5，C=2，g=0.01以及K=3。此外，本文所有结果均是在3.20 GHz/4.0 GB的PC机上利用MATLAB2012a软件编程实现。

3.3 结果与分析

对于6种不同不平衡数据集的3种评价机制的实验对比效果如表4所示。分析表4可知：（1）在不平衡数据集下，传统的SVM算法效果最差，甚至有的数据集中G-mean的值为0，特别是样本集严重失衡时，这是因为分类超平面向正类样本方向发生了严重的偏移，其他算法作为SVM算法的改进形式，使分类超平面偏回负类样本方向，使得分类效果获得提升。（2）传统的DEC算法仅考虑到了样本平衡性的影响，没有考虑样本中噪声或野点影响；相反传统的FSVM算法仅考虑到了样本噪声或野点影响，而忽略了样本平衡性的影响。故在不平衡数据集中传统的DEC与FSVM算法的分类效果提升不是很明显，特别是SEN与G-mean两个评价机制较低，即这两种算法对于分类超平面的向负类偏移影响较小。（3）DEC-FSVM算法将传统的DEC与FSVM方式相结合，融合了两种算法的优点，分类效果得到进一步提升，尤其是SEN或G-mean。（4）DEC-FSVM-Ju算法是在DEC-FSVM算法基础上进行改进，相比DEC-FSVM算法，其分类效果亦有提升，这是因为在设置模糊隶属度函数时DEC-FSVM算法仅考虑了样本到达类中心的距离，而DEC-FSVM-Ju算法考虑样本到类中心距离的同时还考虑了样本的K-近邻域的密度。（5）同样地，DEC-IFSVM作为DEC-FSVM-Ju的改进算法，分类效果亦有提升，这是因为DEC-IFSVM算法除了考虑样本到类中心的距离以及样本的K-近邻域密度外，还考虑到了样本的信息量，在设计模糊隶属度函数时给予样本不同的权值，这样可以赋予支持向量较大的权值，故分类效果进一步提升。（6）对比PSO优化前后的DEC-IFSVM算法可知，经过PSO参数优化后的DEC-IFSVM算法，相比优化前的算法对6种不平衡数据集在分类器的分类效果均有较大提升。

综上，本文所提的算法在综合考虑样本到类中心距离、K-近邻域密度以及样本的信息量设计模糊隶属度函数，并将其与DEC算法相结合，最终引入的参数经过PSO算法优化，与现有的算法相比在不同空间结构以及不同维度的不平衡数据集中具有更好的分类性能。

4 分类器鲁棒性的对比

为了进一步说明本文所提算法的优越性，对本文所有算法的鲁棒性进行比较。本文采用文献[23]中所提算法鲁棒性的评价方式，即算法m在某一特定数据集上的鲁棒性为用该算法求解目标问题时的相对性能，文中选取G-mean值作为不平衡数据分类效果鲁棒性的比较值，求解文中所有算法G-mean值的相对性能，此相对性能的求解算法为

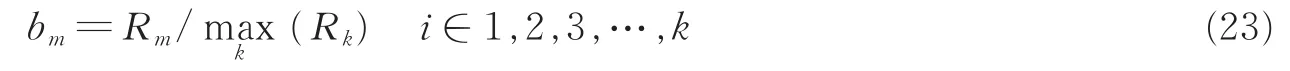
式中：Rm为算法m在某一数据集的Adjusted rand index值；bm为算法m鲁棒性的相对性能。由式（23）可知，当某一算法在特定数据集上表现最好时bm的值即为1，而其他算法bm≤1，且bm的值越大，算法的相对性能就越好。故算法m在不同数据集的鲁棒性可以利用表示，其中l为算法的总数，且本文的算法总数为7。同样的值越大代表该算法的综合鲁棒性越强。利用上述方法求解本文7种算法在6种平衡数据集上G-mean值的鲁棒性，其结果如图3所示。

分析图3可知：（1）传统的SVM算法S-ARI的值远小于其余算法，证明SVM算法的鲁棒性最差；

（2）分析FSVM与DEC算法的S-ARI值可知：FSVM与DEC算法分类器的总体效果不是很理想，DEC-FSVM算法相比FSVM与DEC算法鲁棒性进一步增强，显示了综合考虑样本距离以及不平衡度的优势；（3）DEC-IFSVM作为DEC-FSVM-Ju的改进算法，其S-ARI值有所增加，证明鲁棒性增强不够明显，这是由于算法引入参数增加时，算法复杂度增加且初始参数不是最优值，导致结果不明显；（4）本文所提的PSO-DEC-IFSVM算法对DEC-IFSVM算法引入的参数进行优化，其S-ARI值最大为6，明显大于DEC-IFSVM算法以及其他算法，故在不同的不平衡数据集上均有最好的鲁棒性。

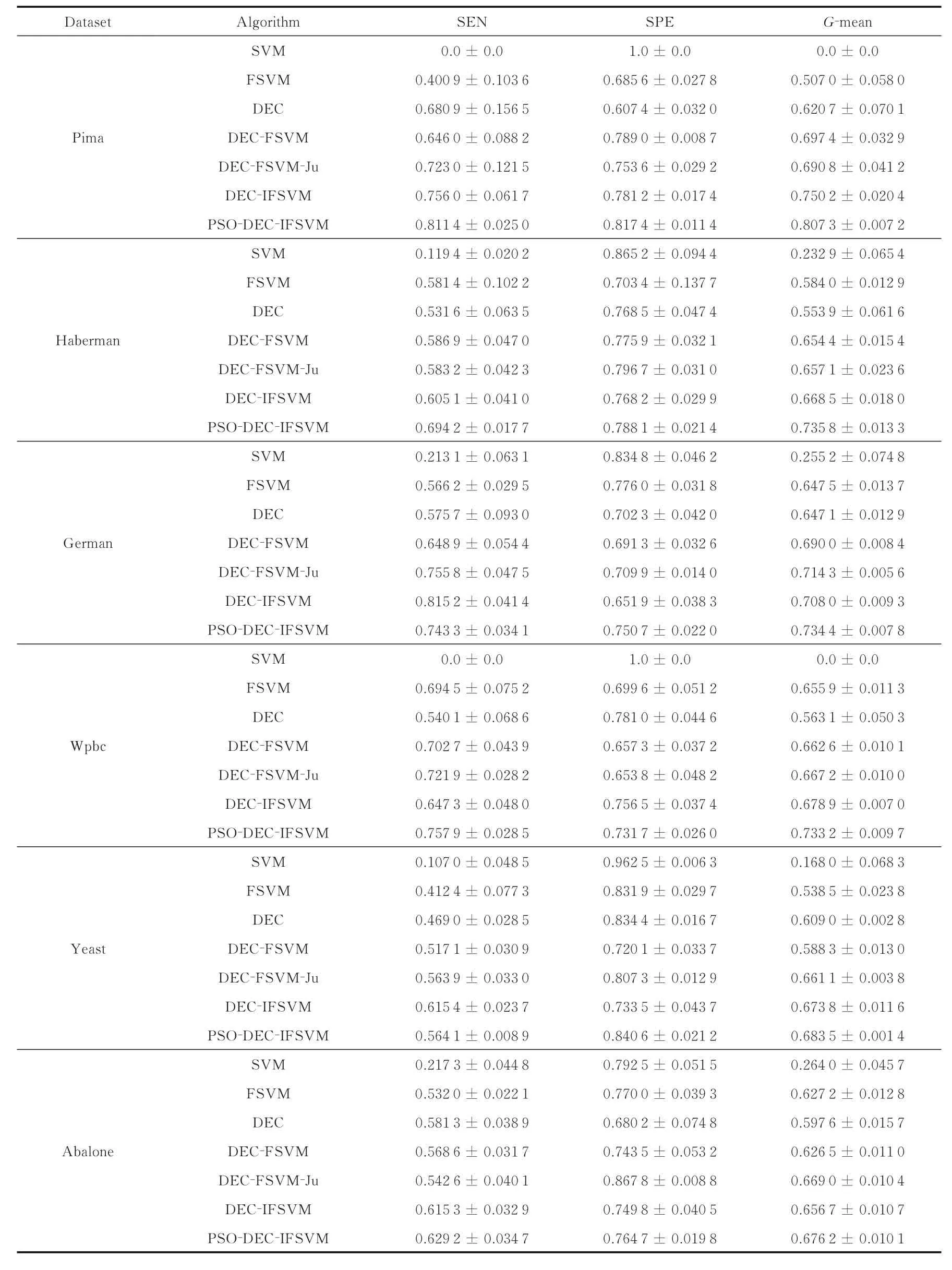
表4 6种不平衡数据集下运用各类算法分类的效果Tab.4 Classification effect of different algorithms in the six kinds of unbalanced data sets

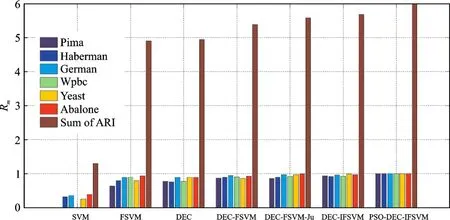
图3 不平衡数据集下7种算法G-mean值的鲁棒性比较Fig.3 Robustness comparison of G-mean value of seven algorithms under Unbalanced data sets

5 结束语

针对传统的模糊支持向量机在不平衡数据集下分类效果不够明显、引入的参数未做优化等缺点，本文提出一种新型的基于粒子群优化的改进支持向量机算法（PSO-DEC-IFSVM）。该算法在设计模糊隶属函数时，综合考虑训练样本到期类中心的间距与样本周围的紧密度以及样本的信息量，并将其与DEC算法相结合，最后利用粒子群算法对DEC-IFSVM算法引入的K，α，M，C以及g五个参数进行优化。实验证明：本文算法相比已有的FSVM算法，正负类的分类精度进一步增加，且此算法拥有更好的鲁棒性。结果证明：本文算法可以更好地降低样本集中含有噪声或野点影响，同时，可以更好地应对数据集不平衡问题。故此算法为不平衡数据的分类问题提供了一个重要的理论模型，该模型可以应用于机械故障诊断、医疗诊断等异常诊断领域，因为在这些领域中故障数据收集相对困难，极易形成不平衡数据集，且数据集中很可能含有噪声或者野点。

本文在利用粒子群算法对DEC-IFSVM分类器进行参数寻优时，仅将分类器的综合评价机制（G-mean）作为优化目标，这可能会导致正负类分类准确率（SEN，SPE）不一定同时比优化前效果理想，所以将SEN，SPE，G-mean同时作为优化目标进行协同优化，即：寻求一种适用于多目标寻优的智能算法，将是课题组下一步的研究重点。