电磁矢量阵中基于PARALIND分解的相干DOA估计算法

徐 乐 张小飞 林新平 周梦婕

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

对于空间中所传播的电磁信号，除了接收方向外，信号极化参数也是一类经常需要考虑的信息。普通的天线所组成的信号接收阵列通常只能从中得到信号的角度信息，无法从中提取出信号的极化状态。而由电磁矢量传感器所组成的电磁矢量阵，在监测入射信号强度的同时，还能够有效地感应其中所包含的磁场分量和电场分量信息。与普通天线阵列相比，电磁矢量传感器能够有效地分辨信号的极化信息，在系统检测能力、极化多址能力和抗干扰能力等方面，都有较大的优势[1-2]。

在传统的波达方向(Direction of arrival,DOA)估计算法的研究基础上，国内外学者们已经提出了众多关于电磁矢量阵多参数估计的算法。其中，文献[3]将借助旋转不变性进行信号参数估计(Estimation of signal parameters via rotational invariance techniques,ESPRIT)算法运用到了电磁矢量传感器中，实现了接收信号角度与极化参数的估计。文献[4]将多重信号分类(Multiple signal classification,MUSIC)算法进行推广，实现了角度和极化参数的联合估计。文献[5]对传统MUSIC算法进行了改进，提出了一种电磁矢量阵中低复杂度的降维MUSIC算法。另外，电磁矢量传感器也被运用到了多输入多输出(Multiple-input multiple-output,MIMO)雷达的信号参数估计算法研究中[6-7]。

然而，在实际应用中由于传播环境的复杂性，接收阵列包括电磁矢量传感器所接收的信号中有相干信号的存在。信号之间的相干性会造成阵列所接收信号协方差矩阵的亏秩[8]，由此,上述的许多算法便不再适用于对这种相干信源进行多参数估计。关于相干信源多参数估计，学者们已经提出了许多有效算法[9-13]，例如Toeplitz矩阵重构算法[9]、最大似然算法[10]以及基于前后向平滑(Forward backward spatial smoothing,FBSS)的FBSS-ESPRIT算法和FBSS-传播算子(Propagator method,PM)算法[11]。

三线性分解，又称为平行因子(Parallel factor,PARAFAC)模型，最早于生理学中提出，用于对多维数据的分析[14]。近年来，该技术被成功地运用到信号处理领域。基于PARAFAC模型框架，文献[15]提出一种在电磁矢量阵中，基于PARAFAC分解的角度和极化参数联合估计算法。该算法利用PARAFAC模型分解的唯一性，能够得到配对的角度和极化参数估计，拥有较好的参数估计性能。然而如同上述算法一样，该算法同样无法对相干信源参数作出有效估计。

平行线性相关剖面模型（Parallel profiles with linear dependencies,PARALIND）可以看作是平行因子模型的扩展[16-18]，该方法能够有效解决相干信源的多参数估计问题。文献[17]将声矢量传感器与PARALIND模型相结合，解决了声矢量传感器阵列中相干信号DOA估计问题。文献[18]则将PARALIND模型应用到了MIMO雷达中，解决了MIMO雷达中的相干信号角度估计问题。

本文将PARALIND模型与电磁矢量阵列相结合，提出了一种线性电磁矢量阵中基于PARALIND分解的相干DOA估计算法。相比于文献[15]，本文所做的工作主要有以下贡献：(1)对电磁矢量传感器阵列所接收的相干信号进行建模，将电磁矢量阵中的PARAFAC模型扩展到PARALIND模型；(2)由PARALIND模型的分解得到信号的角度估计，解决了电磁矢量阵中相干信号的参数估计问题，并详细描述了算法的完整过程。

本文算法在进行接收信号DOA估计的同时，还能够得到信号的相干关系矩阵。另外，该算法对均匀线阵和非均匀线阵都适用，其角度估计性能优于传统的FBSS-ESPRIT算法和FBSS-PM算法。对于角度相隔很小的相干信源，该算法也能够进行有效估计。

1 数据模型

考虑一个由M个电磁矢量传感器组成的线性阵列，第m个接收天线与参考阵元(m=1)之间的距离为dm(m=1,2,…,M)。假设有K个远场信号入射到该阵列，对于第k个目标，θk，γk和ηk分别是其到达角、极化角和极化相位。

对于电磁矢量传感器，假设入射信源b(t)，其仰角和方位角分别为θ和φ，极化参数分别为γ和η，则对于阵列中的第m个传感器，t时刻的输出为[15]

式中s为极化矢量，包含有信号极化参数和角度信息，其表达式为

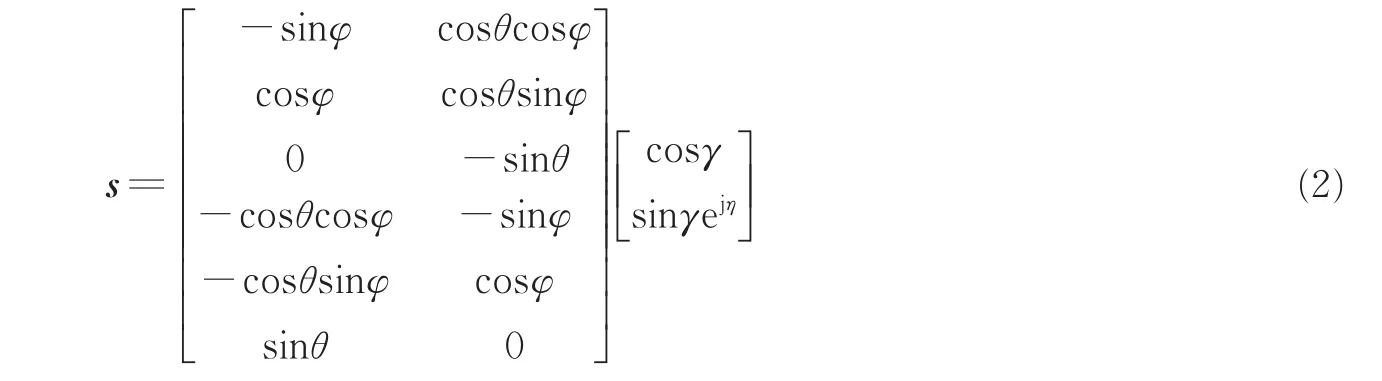
由于本文研究的阵列为线性阵列，因此接收信号方位角φk=90∘,k=1,2,…,K。

对于入射的K个信源，定义极化矩阵S=[s1,s2,…,sK]∈C6×K，其中sk=[-cosγk,cosθksinγkexp(jηk),-sinθksinγkexp(jηk),-sinγkexp(jηk),-cosθkcosγk,sinφkcosγk]T∈C6×1。

根据文献[19]，整个电磁矢量传感器阵列t时刻的接收信号可以表示为

式中：“∘”表示 Khatri-Rao 积，b0(t)=[b1(t),b2(t),…,bK(t)]T∈ CK×1，A=[a(θ1),a(θ2),…,a(θK)]为整个阵列的方向矩阵 ，a(θk)=[1,exp(-j2πd2sinθk/λ),…,exp(-j2πdMsinθk/λ)]T∈ CM×1，n(t)∈C6M×1代表独立、零均值高斯白噪声。

对于J个快拍，整个阵列接收数据～X∈C6M×J可以表示为

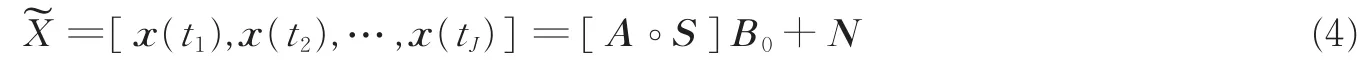
假设入射到阵列中的K个信源中，最多可以找到K1个互不相干的信源，则式(4)中的接收信号可以表示为

式中：B∈CK1×J是K个互不相干信源的信源矢量，Γ∈CK×K1为相干系数矩阵，且满足ΓB=B。 根

10据文献[16]，式(5)中的相干信号接收数据可以转化为PARALIND模型，该模型可以看作为三线性模型的推广，可以有效地用于相干信号的参数估计。

2 相干DDOOAA估计算法

2.1PARAALLIINNDD分解

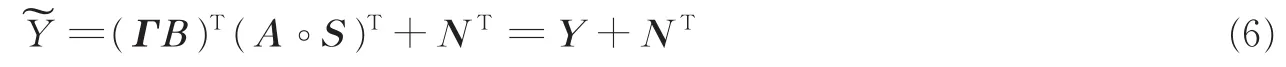
式中：Y=(ΓB)T(A∘S)T为无噪接收信号。式(6)中的接收信号模型即为PARALIND模型[16]，其最小二乘目标函数为

式中：‖·‖F表示Forbenius范数。在无噪声环境下有

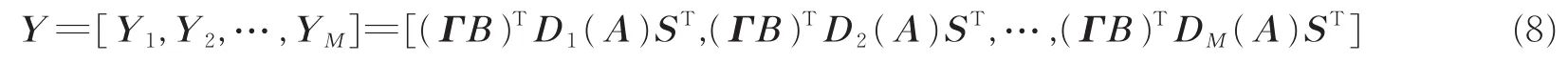
式中：Dn(A)表示取矩阵A第n行元素组成的对角矩阵，Yn=(ΓB)TDn(A)ST∈CJ×6,n=1,2,…,M。

向量化Yn得到[17]

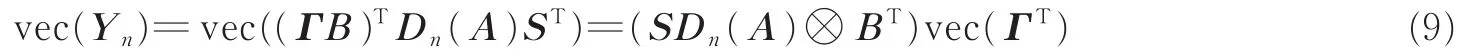
式中：“⊗”表示Kronecker积，将这M个向量堆叠起来为

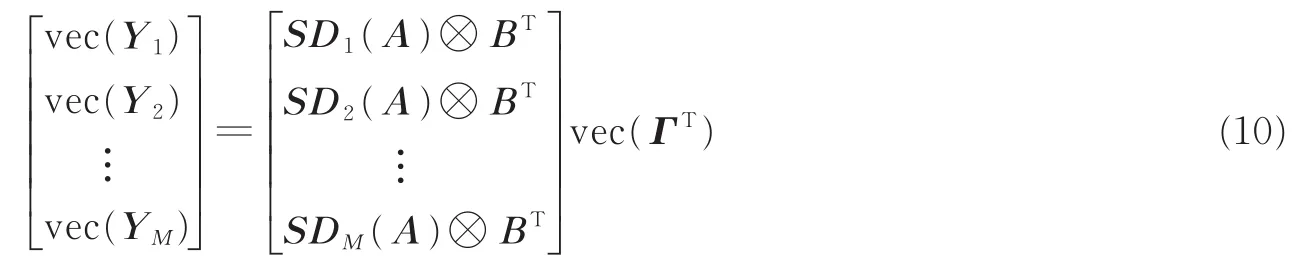
式(10)也可以表示为

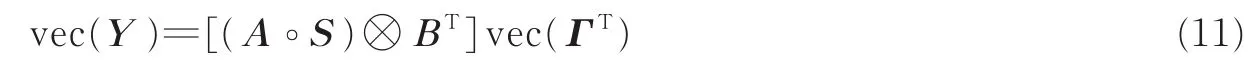
在噪声存在情况下，由式(11)可得

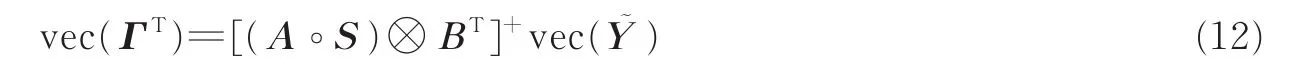
计算出vec(ΓT)后，将其转换为原来的矩阵形式即可得到矩阵Γ。

根据式(7)，BT的最小二乘更新为

根据式(8)有

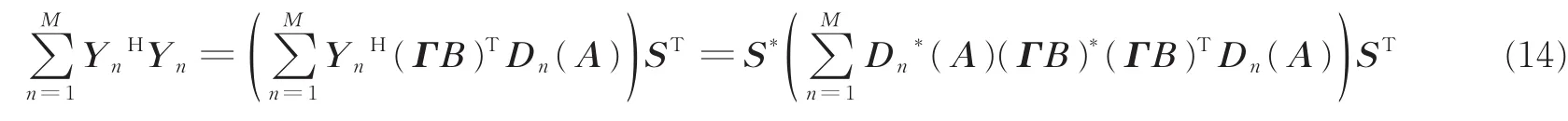
式中：S为满秩矩阵，通过下式即可获得矩阵S*的值

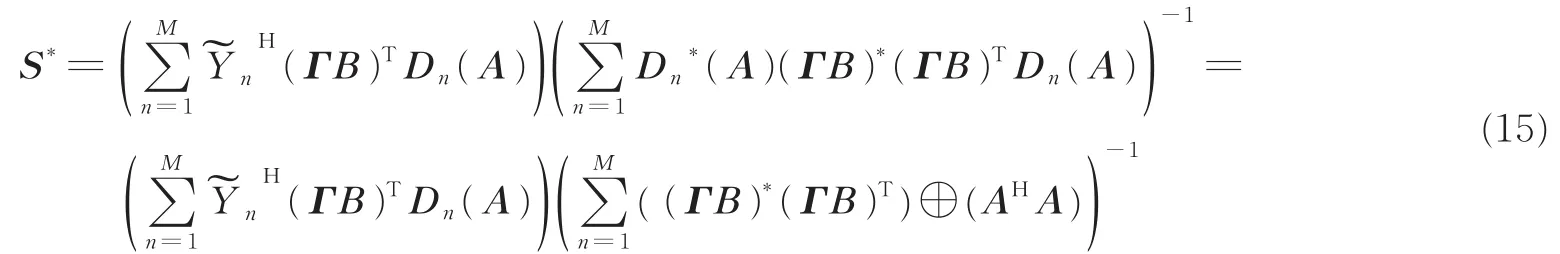
根据式(8)中的子阵，也可以得到

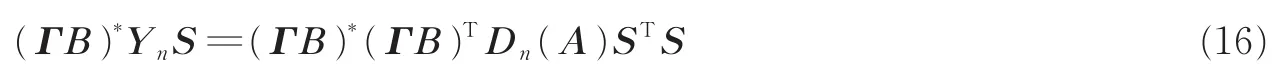
取式(16)两边对角元素有

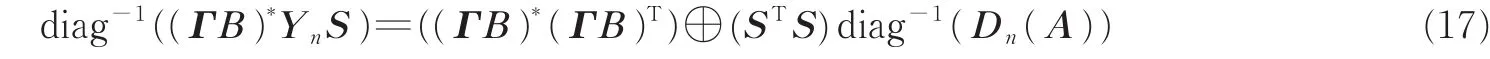
式中：diag-1(·)表示取矩阵的对角元素组成的列向量。根据式(17)，在噪声环境中

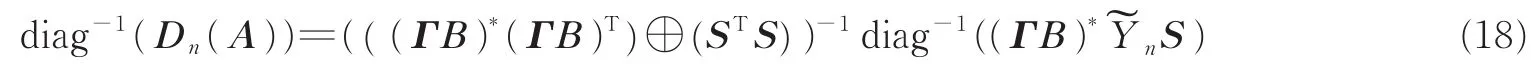
通过diag-1(Dn(A)),n=1,2,…,M的值即可求得矩阵A。

上面的推导已经给出了完整的PARALIND分解推导过程。定义其中，和分别表示Γ，B，A和S的估计值。PARALIND模型中的最小二乘冗余和(Sum of squared re-siduals,SSR)可以定义为其中eji表示矩阵E的第 (j,i)元素。根据式(12，13，15，18)，重复地迭代更新S,B,Γ和A的估计值，直到SSR小于某个设定的门限值即可认为该迭代收敛，此时得到的和即为S,B,Γ和A的最终估计值。

2.2 PARAALLIINNDD分解的唯一性

根据文献[16]推导PARALIND分解的唯一性。对式(8)中的接收信号模型进行初等行列变换，可以得到另外一个矩阵重排形式

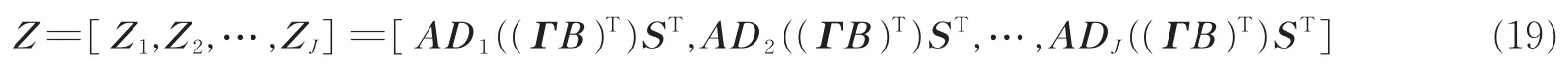
式(19)中的任意两个切片Zi和Zj(i≠j)可以表示为

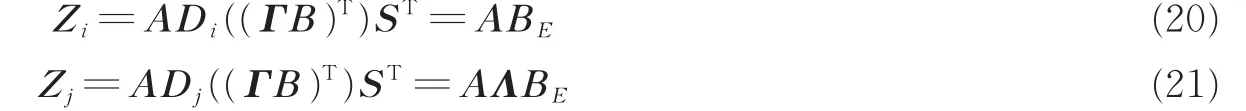
式中：BE=Di((ΓB)T)ST，Λ=Dj((ΓB)T)((ΓB)T)是一个对角矩阵。将这两个切片堆叠有

式中：矩阵BE是列满秩的，令U为矩阵最大的K个左奇异向量构成的矩阵，则根据式(22)有其中，span(U)为矩阵U的子空间，由U的特征向量构成。由于U和张成的子空间是相等的，因此存在一个非奇异矩阵T使得

计算U1自相关矩阵以及U1，U2互相关矩阵，有

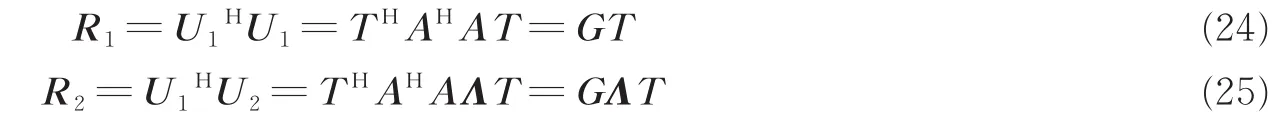
式中：G=THAHA。根据式(24，25)有

由式(26)可知，Λ和G分别由R2的特征值和对应的特征向量构成。忽略特征值的顺序时，Λ是唯一确定的，进而G是可辨识的。最后通过式(22—24)可得T=G-1R1，A=U1T-1，BE=A+Zi，ST=((ΓB)T)BE。

利用上述PARALIND分解，最终可以得到矩阵A的估计为

式中：Π表示列置换矩阵；Δ为对角矩阵，由尺度模糊系数构成；W为估计误差。其中尺度模糊可以利用归一化方法消除。

2.3 相干DDOOAA估计

通过2.2节中的PARALIND分解，得到了方向矩阵A的估计值，假设第k列为(θk)，先对其归一化，使其首项为1，然后定义

利用最小二乘法则估计目标角度[15]，假设ck为最小二乘解，则ck满足

式中

由式(29)可以得到ck的估计为

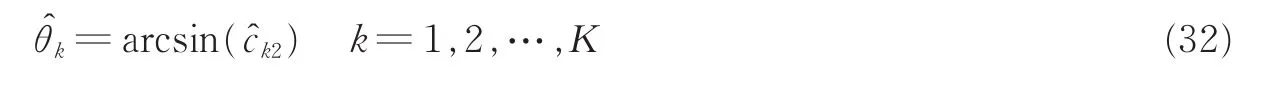
式中arcsin(·)表示反正弦函数。

2.4 算法流程及优点、复杂度分析

上述推导已经给出了线性电磁矢量阵中基于PARALIND分解的相干DOA估计算法的完整过程。该算法主要有以下3个步骤：

(2)根据式(12，13，15，18)，重复迭代更新矩阵和的值，直到 SSR 小于设定的门限值；

(3)根据式(29—32)，利用最小二乘算法，由A的估计值，计算接收信号的DOA估计。

根据上述步骤分析该算法复杂度。M，J，K和K1分别为阵列中的阵元数、快拍数、信源数和非相干信源数。本文中的PARALIND算法每次迭代的复杂度为O(6MJ(2K2K12+2KK1+2K+K1)+6M(2K12+K2+KK1+2K)+K2(JM+J+M2+M+8)+K3K13+2K3+K13+KK1J(M+1))[18]。本文算法中PARALIND分解的迭代次数约为几十次[17]，与FBSS-ESPRIT算法和FBSS-PM算法相比，本文中的算法复杂度高。

本文PARALIND算法的优点有：

(1)本文算法能够对电磁矢量阵中的相干信号DOA进行估计，并且可以同时得到相应的相干关系矩阵。

(2)本文算法角度估计性能优于传统的用于解相干的FBSS-ESPRIT算法及FBSS-PM算法。

(3)本文算法适用于均匀线阵和非均匀线阵，而FBSS-ESPRIT算法和FBSS-PM算法只能用于均匀线阵。

3 仿真结果

在仿真中，假设远场空间有3个信源，第1个和第3个信源相干，而第2个与另外两个不相干，相干关系矩阵为

假设 3个信源的到达角分别为θ1=5°，θ2=15°，θ3=25°。M，J，K分别表示阵元数、快拍数和信源数。在下面的仿真中，利用高斯随机矩阵对PARALIND迭代分解中的参数矩阵进行初始化，设定SSR=10-5，并利用1 000次蒙特卡洛仿真中的角度估计均方根误差(Root mean squares error,RMSE)去评估算法的性能。其中，角度估计的RMSE定义为

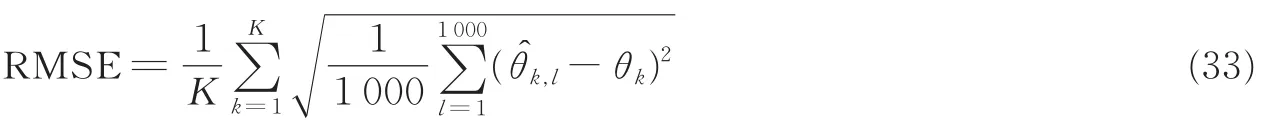
式中：θk表示第k个目标的准确到达角；θ^k,l是第l次蒙特卡洛仿真中θk的估计值。

图1，图2为本文所提出的算法在信噪比(Signal noise ratio,SNR)为15 dB下，仿真100次的角度估计结果分布图。两次仿真中阵元数M=15、快拍数J=200。其中仿真1采用均匀线阵，相邻阵元间距为λ/2，仿真2采用非均匀线阵，各阵元与参考阵元间的间 距为d=[0,0.25,0.7,1.15,1.65,2,2.4,2.85,3.35,3.75,4,4.4,4.75,4.9,5.1]λ。从图 1、图2可以看出本文算法对均匀线阵和非均匀线阵都能得到较准确的角度估计结果。

图3为本文算法与FBSS-ESPRIT算法以及FBSS-PM算法的对比仿真结果，仿真中接收阵列采用均匀线阵，相邻阵元间距为λ/2，M=10，J=100。从图3可以看出，对于相干信号的角度估计，PARALIND算法性能优于两个传统的前后向平滑算法。

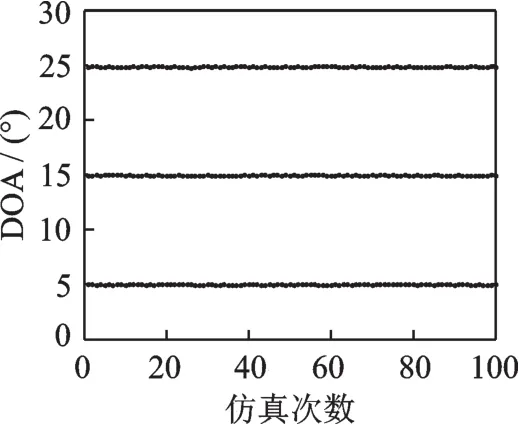
图1 均匀线阵下PARALIND算法角度估计结果Fig.1 Angle estimation of PARALIND algorithm foruniform linear array

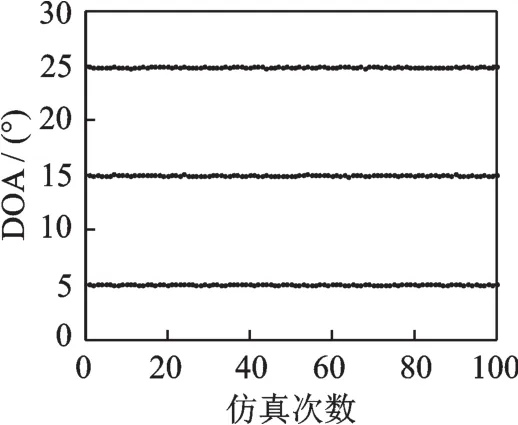
图2 非均匀线阵下PARALIND算法角度估计结果Fig.2 Angle estimation of PARALIND algorithm for non-uniform linear array

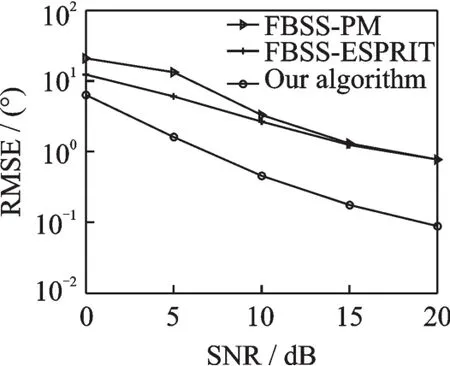
图3 3种相干信号算法角度估计性能对比Fig.3 Angle estimation performance comparison of three algorithms for coherent signals

图4为本文算法在接收信号全部为非相干信号时，与ESPRIT算法、PM算法以及PARAFAC算法的对比仿真结果，仿真中接收阵列为间距λ/2的均匀线阵，M=12，J=100。从图4中可以看出，对于非相干信号，本文中的PARALIND算法估计性能优于其他3种算法。

图5给出了本文算法角度估计性能在不同阵元数下的仿真结果，仿真中快拍数J=100，接收阵列为阵元间距λ/2的均匀线阵。从图5可以看出，该算法性能随着阵元数M的增大而提高，其原因是阵元的增多提高了空间分集增益。

图6为本文算法在不同快拍数下的仿真结果，仿真6中阵元数M=8，阵元间距d=[0,0.25,0.7,1.15,1.65,2,2.4,2.85]λ。从图6中可知，该算法角度估计误差随着快拍数的增大而减小，其原因为快拍数增大提高了时间分集增益。

假设有两个角度相近的相干信号源入射到该阵列，信号到达角分别为θ1=5°，θ2=7°，M，J及SNR设置同图1，本文所提算法仿真100次的角度估计结果分布图如图7所示。从图7中可以看出，两组角度估计结果区分度较高，说明该算法对角度相隔较近的相干信号也能进行有效的辨识与估计。

假设有多个相干信号入射到间距为λ/2的均匀电磁矢量阵列，信源数K=6，信号到达角为θ=[5°,10°,15°,20°,25°,30°]，其中信号 1，5，6为第 1组相干信号，信号 2，4为第 2 组相干信号。设置阵元数M=8，快拍数J=400，SNR=20。图8为本文所提算法仿真100次的角度估计结果分布图，从图8可以看出，对于多个相干信源，本文算法也能进行有效区分，并得到较准确的角度估计。同时，由于相干信源增多，信号间的相互干扰增强，该算法对信号的角度估计性能略有下降。

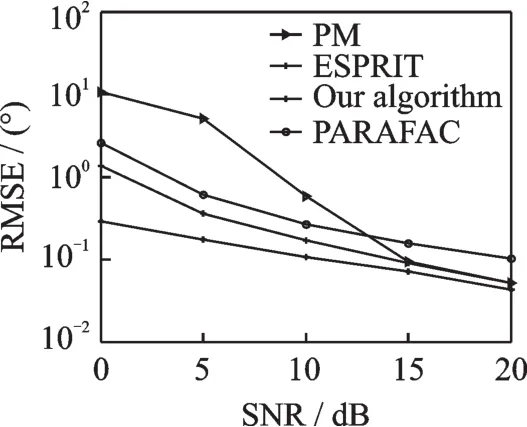
图4 4种非相干信号算法角度估计性能对比Fig.4 Angle estimation performance comparison of four algorithms for incoherent signals

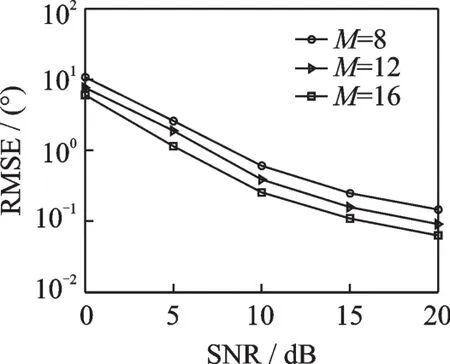
图5 不同阵元数下的算法估计性能Fig.5 Angle estimation performance under different number of sensors

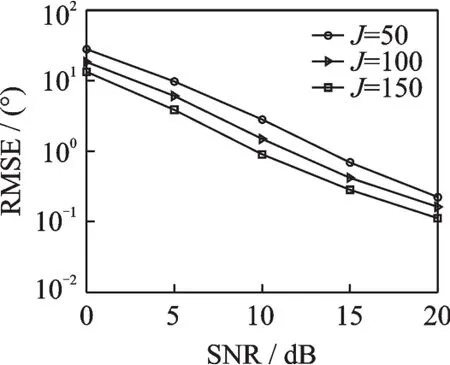
图6 不同快拍数下的算法估计性能Fig.6 Angle estimation performance under different snapshots

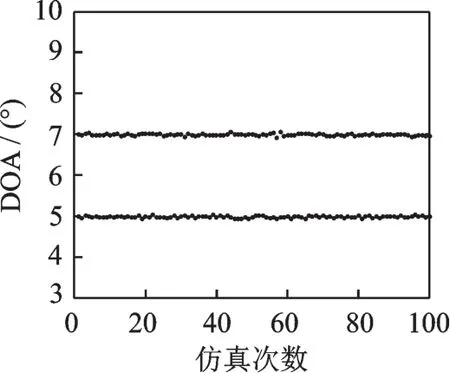
图7 角度相近的相干信源估计结果Fig.7 Angle estimation for closely spaced coherent sources

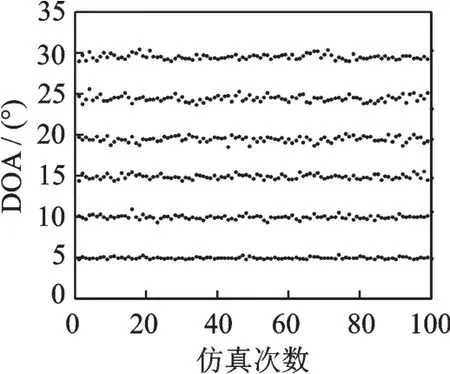
图8 多组相干信源角度估计结果Fig.8 Angle estimation for multiple coherent sources

4 结束语

本文将PARALIND模型与电磁矢量传感器阵列相结合，解决了线性电磁矢量阵中相干信号DOA估计问题。仿真表明，该算法对于均匀线阵或非均匀线阵都适用，同时能得到信号的相干关系矩阵。从仿真结果可以看出，对于相干信号该算法角度估计性能优于传统的FBSS-ESPRIT算法以及FBSSPM算法，而对于非相干信号，该算法角度性能也好于常用的ESPRIT算法、PM算法以及PARAFAC算法。同时，该算法能有效区分角度相隔较近的相干信源，并得到较准确的DOA估计结果。